Bonn THDM 2013: Program
Contents |
[edit] 1 Introduction
[edit] 1.1 K0 and Wall's finiteness obstruction
Speaker: WL
Slides: Lecture 1
Abstract: We introduce the projective class group 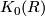 . We explain computations for
special rings, e.g., fields, complex group rings for finite groups. We state Swan's
Theorem which relates the projective class group of the ring
. We explain computations for
special rings, e.g., fields, complex group rings for finite groups. We state Swan's
Theorem which relates the projective class group of the ring 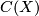 of continuous
of continuous
 -valued functions to the Grothendieck group of vector bundles over
-valued functions to the Grothendieck group of vector bundles over  , if
, if  is a
finite
is a
finite  -complex. We discuss Wall's finiteness obstruction which decides whether a finitely
dominated
-complex. We discuss Wall's finiteness obstruction which decides whether a finitely
dominated  -complex is homotopy equivalent to a finite
-complex is homotopy equivalent to a finite  -complex and takes values in
the projective class group of the integral group ring of the fundamental group.
-complex and takes values in
the projective class group of the integral group ring of the fundamental group.
Exercises: K-group, zeroth (Ex), Finitely dominated CW complexes (Ex)
References: [Lück1987], [Lück1989], [Mislin1995], [Ranicki1985], [Rosenberg1994], [Wall1965a], [Wall1966b]
[edit] 1.2 K1 and Whitehead torsion
Speaker: WL
Slides: Lecture 2
Abstract: We introduce 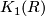 and the Whitehead group
and the Whitehead group 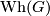 .
We define the Whitehead torsion of a homotopy equivalence of finite connected
.
We define the Whitehead torsion of a homotopy equivalence of finite connected  -complexes.
We discuss the algebraic and topological significance of these notions, in particular the
-complexes.
We discuss the algebraic and topological significance of these notions, in particular the  -cobordism theorem. We briefly introduce the surgery program.
Finally we introduce negative
-cobordism theorem. We briefly introduce the surgery program.
Finally we introduce negative  -theory and the Bass-Heller-Swan decomposition.
-theory and the Bass-Heller-Swan decomposition.
Exercises: K-group, first (Ex), Whitehead torsion (Ex), Reidemeister torsion (Ex), K-group, all (Ex)
References: [Cohen1973], [Lück1989], [Lück2002], [Milnor1966], [Ranicki1985a], [Ranicki1987], [Rosenberg1994]
[edit] 1.3 Normal maps and surgery below the middle dimension
Speaker: SA-F
Slides: Lecture 3
Abstract: We begin with a discussion of the surgery programme, motivating the definition of a degree one normal map. The surgery method proceeds via a two stage obstruction theory. We will primarily concentrate on the second  -theoretic obstruction which corresponds to the question of when a degree one normal map is normal bordant to a homotopy equivalence. Introducing surgery and the surgery step we explain how surgery can always be performed below the middle dimension. If surgery can also be done in the middle dimension Poincaré duality and Whitehead's theorem give us a homotopy equivalence. As we shall see in the next two lectures this cannot always be done... .
-theoretic obstruction which corresponds to the question of when a degree one normal map is normal bordant to a homotopy equivalence. Introducing surgery and the surgery step we explain how surgery can always be performed below the middle dimension. If surgery can also be done in the middle dimension Poincaré duality and Whitehead's theorem give us a homotopy equivalence. As we shall see in the next two lectures this cannot always be done... .
Exercises: Homology braid I (Ex), Homology braid II (Ex), Dehn surgery (Ex), Structure set (Ex)
References: [Ranicki2002, Chapters 1 & 10], [Lück2001, Chapter 3], [Wall1970b, Chapter 1], [Kervaire&Milnor1963], [Browder1972]
[edit] 1.4 The even-dimensional surgery obstruction
Speaker: SA-F
Slides: Lecture 4
Abstract: We begin by explaining how we cannot necessarily do surgery on an element 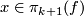 in the middle dimension if
in the middle dimension if 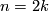 as immersions may not be regularly homotopic to embeddings. For
as immersions may not be regularly homotopic to embeddings. For 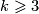 we can do surgery if the self-intersection number of the immersion is trivial. This motivates us to study intersections and self-intersections which leads to the definition of the
we can do surgery if the self-intersection number of the immersion is trivial. This motivates us to study intersections and self-intersections which leads to the definition of the 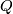 -groups and Wall's
-groups and Wall's  form. From the geometry we extract the algebraic obstruction to surgery in the middle dimension which lies in the even dimensional
form. From the geometry we extract the algebraic obstruction to surgery in the middle dimension which lies in the even dimensional  -groups. For
-groups. For 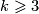 the surgery obstruction vanishes if and only if we can do finitely many surgeries on our degree one normal map to obtain a degree one normal map covering a homotopy equivalence.
the surgery obstruction vanishes if and only if we can do finitely many surgeries on our degree one normal map to obtain a degree one normal map covering a homotopy equivalence.
Exercises: Surgery obstruction, signature (Ex), Surgery obstruction, Arf-invariant (Ex), E8-form (Ex), Even dimensional surgery obstruction (Ex)
References: [Ranicki2002, Chapter 11], [Lück2001, Chapter 4, 4.1-4.3], [Wall1970b, Chapters 5 & 8]
[edit] 1.5 The odd-dimensional surgery obstruction
Speaker: SA-F
Slides: Lecture 5
Abstract: We begin by discussing how even though we can always do surgery on an element 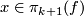 for
for 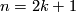 the surgery does not necessarily make the surgery kernel smaller as different choices of framing have different results. We discuss Heegaard splittings and from the geometry motivate the definition of quadratic formations. We introduce the kernel formation associated to a Heegaard splitting of a degree one normal map and the notion of a presentation. We characterise algebraically when we can do surgery to kill
the surgery does not necessarily make the surgery kernel smaller as different choices of framing have different results. We discuss Heegaard splittings and from the geometry motivate the definition of quadratic formations. We introduce the kernel formation associated to a Heegaard splitting of a degree one normal map and the notion of a presentation. We characterise algebraically when we can do surgery to kill 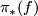 and this leads to the definition of the odd-dimensional
and this leads to the definition of the odd-dimensional  -groups; in dimensions at least five the surgery obstruction vanishes if and only if our degree one normal map is normal bordant to a homotopy equivalence.
-groups; in dimensions at least five the surgery obstruction vanishes if and only if our degree one normal map is normal bordant to a homotopy equivalence.
Exercises: Generator sets and the kernel formation (Ex), Kernel formation (Ex), Presentations (Ex)
References: [Ranicki2002, Chapter 12], [Lück2001, Chapter 4, 4.4-4.6], [Wall1970b, Chapters 6-7], [Wall1963], [Novikov1970], [Ranicki1973]
[edit] 1.6 The geometric surgery exact sequence
Speaker: SA-F
Slides: Lecture 6
Abstract: We begin with a discussion of Wall realisation: if we permit ourselves to consider manifolds with boundary then every surgery obstruction can be realised. We then reach the culmination of the classical surgery programme, namely the surgery exact sequence - the main theoretical tool for the classification of high-dimensional manifolds. We also discuss the simple surgery exact sequence.
Exercises: Normal and tangential structures (Ex), Surgery exact sequence, PL sphere (Ex), Wall realisation (Ex)
References: [Ranicki2002, Chapter 13], [Lück2001, Chapter 5]
[edit] 2 Surgery on smooth manifolds
[edit] 2.1 Homotopy spheres and other examples
Speaker: DC
Slides: Lecture 7
Abstract: We review the Kervaire-Milnor classification of the group  of homotopy spheres, that is the group of diffeomorphism classes oriented closed smooth manifolds homotopy equivalent to the
of homotopy spheres, that is the group of diffeomorphism classes oriented closed smooth manifolds homotopy equivalent to the  -sphere. This classification is equivalent to computing the structure set of
-sphere. This classification is equivalent to computing the structure set of  . We report on what is known about the group
. We report on what is known about the group  . We then consider the problem of classifying homotopy equivalent manifolds up to diffeomorphism and show how this is equivalent to computing the action of the group of self-homotopy equivalences on the structure set. Finally, we present the structure sets of products of spheres and certain Stiefel manifolds as illustrative examples.
. We then consider the problem of classifying homotopy equivalent manifolds up to diffeomorphism and show how this is equivalent to computing the action of the group of self-homotopy equivalences on the structure set. Finally, we present the structure sets of products of spheres and certain Stiefel manifolds as illustrative examples.
Exercises: Homotopy spheres I (Ex), Homotopy spheres II (Ex), Homotopy spheres III (Ex), Inertia group I (Ex), Manifolds cross a circle (Ex)
References: [Kervaire&Milnor1963], [Levine1983], [Brumfiel1968], [Crowley&Lück&Macko2013, Ch.6], [Crowley2010]
[edit] 2.2 Normal invariants in detail
Speaker: DC
Slides: Lecture 8
Abstract: We present the Browder-Sullivan theory of normal invariants of degree one normal maps in detail and in particular show how Spanier-Whitehead duality is used to convert normal bordism classes into maps to certain classifying spaces. We then give several examples including self-homotopy equivalences with non-trivial normal invariant which lead to Poincaré complexes whose Spivak normal fibration does not admit a vector bundle reduction.
Exercises: Reducible Poincaré Complexes (Ex), Non-reducible Spivak Normal Fibrations (Ex), Normal invariants of products (Ex), Tangential homotopy equivalences (Ex)
References: [Browder1972, II, §4], [Madsen&Taylor&Williams1980], [Crowley&Hambleton2013, §6, §7]
[edit] 2.3 Smoothing and surgery
Speaker: DC
Slides: Lecture 9, Slides: Lecture 10
Abstract: We review the main results of smoothing theory, in particular the isomorphism 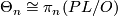 , and then state the relationship of smoothing theory to the surgery exact sequence. We give examples of non-smoothable topological manifolds due to Kervaire and also smooth manifolds with a unique smooth structure due to Kreck. We then define the geometric Kervaire-Milnor braid and the homotopy Kervaire-Milnor braid and sketch the proof that these braids are isomorphic. Finally, we look at the action of the surgery exact sequence of the sphere on the surgery exact sequence of a general manifold and define the inertia group and homotopy inertia group.
, and then state the relationship of smoothing theory to the surgery exact sequence. We give examples of non-smoothable topological manifolds due to Kervaire and also smooth manifolds with a unique smooth structure due to Kreck. We then define the geometric Kervaire-Milnor braid and the homotopy Kervaire-Milnor braid and sketch the proof that these braids are isomorphic. Finally, we look at the action of the surgery exact sequence of the sphere on the surgery exact sequence of a general manifold and define the inertia group and homotopy inertia group.
Exercises: Kervaire-Milnor Braid (Ex), Inertia group II (Ex), Smoothings of products (Ex), Homotopy spheres IV (Ex)
References: [Hirsch&Mazur1974], [Kervaire1960a], [Kreck1984], [Crowley&Lück&Macko2013, §6.7], [Schultz1987]
[edit] 2.4 Classifying spaces for surgery
Speaker: DC
Abstract: We review Sullivan's analysis of the homotopy type of 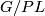 and state its extension
to
and state its extension
to 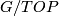 provided by Kirby and Siebenmann. In particular, we review the cohomology classes
provided by Kirby and Siebenmann. In particular, we review the cohomology classes 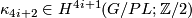 and
and 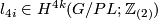 . We then give the simply connected surgery obstruction formula, and state fundamental results of Brumfiel, Madsen and Milgram concerning the canonical homomorphism
. We then give the simply connected surgery obstruction formula, and state fundamental results of Brumfiel, Madsen and Milgram concerning the canonical homomorphism 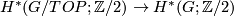 . Finally, we formulate the role of the classes
. Finally, we formulate the role of the classes 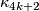 in the Kervaire invariant problem.
in the Kervaire invariant problem.
Exercises: Kappa classes (Ex), Normal maps and submanifolds (Ex), Splitting invariants (Ex)
References: [Madsen&Milgram1979, Ch.4], [Kirby&Siebenmann1977, Essay V], [Brumfiel&Madsen&Milgram1973]
[edit] 3 Algebraic L-theory
[edit] 3.1 L-groups via chain complexes
Speaker: TM
Slides: L-Theory I
Abstract: We introduce symmetric and quadratic structures on chain complexes which are analogues of symmetric and quadratic forms on modules. A non-degeneracy condition yields Poincaré complexes. Further we generalize to structures on chain maps obtaining the notion of a symmetric pair and a quadratic pair and a non-degeneracy assumption on these produces the notion of a cobordism of symmetric and quadratic Poincaré complexes. Cobordism classes then define the promised  -groups. We introduce the technique of algebraic surgery which is the main tool in showing that the
-groups. We introduce the technique of algebraic surgery which is the main tool in showing that the  -groups defined via chain complexes agree with the
-groups defined via chain complexes agree with the  -groups defined via forms and formations.
-groups defined via forms and formations.
Exercises: Equivariant maps (Ex), Forms and chain complexes I (Ex), Structured chain complexes (Ex), Structured chain complexes V (Ex), Structured chain complexes III (Ex)
References: [Ranicki1980], [Ranicki1980a], [Ranicki2002a], [Kühl&Macko&Mole2011], [Crowley&Lück&Macko2013, Chapter 8].
[edit] 3.2 Signatures
Speaker: TM
Slides: L-Theory II
Abstract: We first show that an  -dimensional geometric Poincaré complex defines an
-dimensional geometric Poincaré complex defines an  -dimensional Poincaré symmetric structure on its singular chain complex. Its class in an appropriate
-dimensional Poincaré symmetric structure on its singular chain complex. Its class in an appropriate  -group is called the symmetric signature of that complex. Secondly we show that a degree one normal map between
-group is called the symmetric signature of that complex. Secondly we show that a degree one normal map between  -dimensional geometric Poincaré complexes defines an
-dimensional geometric Poincaré complexes defines an  -dimensional Poincaré quadratic structure on the mapping cone of the Umkehr map, again its class in an appropriate
-dimensional Poincaré quadratic structure on the mapping cone of the Umkehr map, again its class in an appropriate  -group is called the quadratic signature of that map. To obtain it, we introduce the suspension of a symmetric complex and of a quadratic complex and using it we state a condition for refining symmetric structures to quadratic structures. We use
-group is called the quadratic signature of that map. To obtain it, we introduce the suspension of a symmetric complex and of a quadratic complex and using it we state a condition for refining symmetric structures to quadratic structures. We use  -duality from stable homotopy theory to see that the condition is fulfilled for such a degree one normal map. In case our Poincaré complexes are manifolds the resulting complex represents the surgery obstruction in the
-duality from stable homotopy theory to see that the condition is fulfilled for such a degree one normal map. In case our Poincaré complexes are manifolds the resulting complex represents the surgery obstruction in the  -group.
-group.
Exercises: Suspension of a symmetric complex (Ex), Structured chain complexes IV (Ex), S-duality III (Ex), Formations and chain complexes I (Ex), Boundaries of symmetric complexes (Ex)
References: [Ranicki1980], [Ranicki1980a], [Ranicki2002a], [Kühl&Macko&Mole2011], [Crowley&Lück&Macko2013, Chapter 8] and [Browder1972, I §4] for S-duality; see also [Adams1974], [Switzer2002, Ch.14]
[edit] 3.3 L-groups of categories and assembly maps
Speaker: TM
Slides: L-Theory III
Abstract: We generalize the notions from the first two talks to complexes over an arbitrary additive category with chain duality. We define such a chain duality on the category of modules over a simplicial complex. This yields on one hand a construction of the  -spectra. On the other hand imposing a certain local Poincaré condition produces homology of a space with coefficients in an
-spectra. On the other hand imposing a certain local Poincaré condition produces homology of a space with coefficients in an  -theory spectrum. Relaxing the local Poincaré duality to global Poincaré duality produces the assembly map.
-theory spectrum. Relaxing the local Poincaré duality to global Poincaré duality produces the assembly map.
Exercises: Chain duality I (Ex), Chain duality II (Ex), Chain duality III (Ex), Chain duality IV (Ex), Chain duality V (Ex), Chain duality VI (Ex)
References: [Ranicki1992], [Kühl&Macko&Mole2011].
[edit] 3.4 Surgery obstructions and assembly maps
Speaker: TM
Slides: L-Theory IV
Abstract: We generalize the signatures from the second talk in the case when the Poincaré complexes are manifolds to signatures over the categories from the third talk. This produces a map (which turns out to be an isomorphism) from the geometric surgery exact sequence to the algebraic surgery exact sequence. This map identifies the surgery obstruction map with the assembly map.
References: [Ranicki1992], [Kühl&Macko&Mole2011]
[edit] 4 The isomorphism conjectures
[edit] 4.1 The Isomorphism Conjectures in the torsion-free case
Speaker: WL
Slides: Lecture 3
Abstract: We introduce spectra and how they yield homology theories. We state the Farrell-Jones Conjecture and the Baum-Connes Conjecture for torsion free groups and discuss applications of these conjectures, such as the Kaplansky Conjecture and the Borel Conjecture. We explain that the formulations for torsion free groups cannot extend to arbitrary groups.
Exercises: Smash product (Ex), K-groups of oriented surface groups (Ex), Idempotents in group rings (Ex), Borel conjecture in dimensions 1 and 2 (Ex)
References: [Bartels&Lück&Reich2008], [Baum&Connes&Higson1994], [Farrell&Jones1993a], [Kreck&Lück2009], [Lück&Reich2006]
[edit] 4.2 The Isomorphism Conjectures in general
Speaker: WL
Slides: Lecture 4
Abstract: We introduce classifying spaces for families. We define equivariant homology theories and explain how they can be construced by spectra over groupoids. Then we state the Farrell-Jones Conjecture and the Baum-Connes Conjecture in general. We discuss further applications, such as the Novikov Conjecture.
Exercises: Classifying spaces for proper group actions (Ex), Equivariant homology (Ex), K-group, zeroth II (Ex)
References: [Bartels&Lück&Reich2008], [Bartels&Lück&Weinberger2010], [Baum&Connes&Higson1994], [Kreck&Lück2005], [Lück2002a], [Lück2002b], [Lück2005], [Farrell&Jones1993a], [Lück&Reich2006]
[edit] 4.3 Status and methods of proof
Speaker: WL
Slides: Lecture 5
Abstract: We give a status report of the Farrell-Jones Conjecture, discuss open cases and the search for potential counterexamples, and briefly survey the methods of proof.
References: [Bartels2012], [Bartels&Farrell&Lück2011], [Bartels&Lück2012], [Bartels&Lück&Reich2008a], [Bartels&Lück&Reich2008], [Bartels&Lück&Reich&Rueping2012], [Lück2008a]
[edit] 5 References
- [Adams1974] J. F. Adams, Stable homotopy and generalised homology, University of Chicago Press, Chicago, Ill., 1974. MR0402720 (53 #6534) Zbl 0309.55016
- [Bartels&Farrell&Lück2011] A. Bartels, F. Farrell and W. Lück, The Farrell-Jones Conjecture for cocompact lattices in virtually connected Lie groups, (2011). Available at the arXiv:1101.0469v1.
- [Bartels&Lück&Reich&Rueping2012] A. Bartels, W. Lück, H. Reich and H. Rueping, K- and L-theory of group rings over GL_n(Z). To appear in Publ. Math. IHES, (2012). Available at the arXiv:1204.2418.
- [Bartels&Lück&Reich2008] A. Bartels, W. Lück and H. Reich, On the Farrell-Jones Conjecture and its applications, Journal of Topology 1 (2008), 57–86. MR2365652 (2008m:19001) Zbl 1141.19002
- [Bartels&Lück&Reich2008a] A. Bartels, W. Lück and H. Reich, The
 -theoretic Farrell-Jones conjecture for hyperbolic groups, Invent. Math. 172 (2008), no.1, 29–70. MR2385666 (2009c:19002) Zbl 1143.19003
-theoretic Farrell-Jones conjecture for hyperbolic groups, Invent. Math. 172 (2008), no.1, 29–70. MR2385666 (2009c:19002) Zbl 1143.19003
- [Bartels&Lück&Weinberger2010] A. Bartels, W. Lück and S. Weinberger, On hyperbolic groups with spheres as boundary, J. Differential Geom. 86 (2010), no.1, 1–16. MR2772544 (2012b:57003) Zbl 1216.53043
- [Bartels&Lück2012] A. Bartels and W. Lück, The Borel conjecture for hyperbolic and CAT(0)-groups., Ann. of Math. (2) 175 (2012), 631–689. MR2993750 Zbl 06025000
- [Bartels2012] A. Bartels, On proofs of the Farrell-Jones Conjecture, (2012). Available at the arXiv:1210.1044.
- [Baum&Connes&Higson1994] P. Baum, A. Connes and N. Higson, Classifying space for proper actions and
 -theory of group
-theory of group 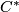 -algebras, In
-algebras, In 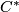 -algebras: 1943–1993 (San Antonio, TX 1993), (1994), 240–291. MR1292018 (96c:46070) Zbl 0830.46061
-algebras: 1943–1993 (San Antonio, TX 1993), (1994), 240–291. MR1292018 (96c:46070) Zbl 0830.46061
- [Browder1972] W. Browder, Surgery on simply-connected manifolds, Springer-Verlag, New York, 1972. MR0358813 (50 #11272) Zbl 0543.57003
- [Brumfiel&Madsen&Milgram1973] G. Brumfiel, I. Madsen and R. J. Milgram,
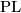 characteristic classes and cobordism, Ann. of Math. (2) 97 (1973), 82–159. MR0310881 (46 #9979) Zbl 0248.57006
characteristic classes and cobordism, Ann. of Math. (2) 97 (1973), 82–159. MR0310881 (46 #9979) Zbl 0248.57006
- [Brumfiel1968] G. Brumfiel, On the homotopy groups of
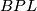 and
and 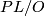 , Ann. of Math. (2) 88 (1968), 291–311. MR0234458 (38 #2775) Zbl 0179.28601
, Ann. of Math. (2) 88 (1968), 291–311. MR0234458 (38 #2775) Zbl 0179.28601
- [Cohen1973] M. M. Cohen, A course in simple-homotopy theory, Springer-Verlag, New York, 1973. MR0362320 (50 #14762) Zbl 0261.57009
- [Crowley&Hambleton2013] D. Crowley and I. Hambleton, Finite group actions on Kervaire manifolds, (2013). Available at the arXiv:1305.6546.
- [Crowley&Lück&Macko2013] D. Crowley, W. Lück and T. Macko, Sugery Theory, Part I, in preparation, Bonn 2013.
- [Crowley2010] D. Crowley, The smooth structure set of
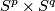 , Geom. Dedicata 148 (2010), 15–33. MR2721618 (2012a:57041) Zbl 1207.57043
, Geom. Dedicata 148 (2010), 15–33. MR2721618 (2012a:57041) Zbl 1207.57043
- [Farrell&Jones1993a] F. T. Farrell and L. E. Jones, Isomorphism conjectures in algebraic
 -theory, J. Amer. Math. Soc. 6 (1993), no.2, 249–297. MR1179537 (93h:57032) Zbl 0798.57018
-theory, J. Amer. Math. Soc. 6 (1993), no.2, 249–297. MR1179537 (93h:57032) Zbl 0798.57018
- [Hirsch&Mazur1974] M. W. Hirsch and B. Mazur, Smoothings of piecewise linear manifolds, Princeton University Press, 1974. MR0415630 (54 #3711) Zbl 0298.57007
- [Kervaire&Milnor1963] M. A. Kervaire and J. W. Milnor, Groups of homotopy spheres. I, Ann. of Math. (2) 77 (1963), 504–537. MR0148075 (26 #5584) Zbl 0115.40505
- [Kervaire1960a] M. A. Kervaire, A manifold which does not admit any differentiable structure, Comment. Math. Helv. 34 (1960), 257–270. MR0139172 (25 #2608) Zbl 0145.20304
- [Kirby&Siebenmann1977] R. C. Kirby and L. C. Siebenmann, Foundational essays on topological manifolds, smoothings, and triangulations, Princeton University Press, Princeton, N.J., 1977. MR0645390 (58 #31082) Zbl 0361.57004
- [Kreck&Lück2005] M. Kreck and W. Lück, The Novikov conjecture, Birkhäuser Verlag, Basel, 2005. MR2117411 (2005i:19003) Zbl 1058.19001
- [Kreck&Lück2009] M. Kreck and W. Lück, Topological rigidity for non-aspherical manifolds, Pure Appl. Math. Q. 5 (2009), no.3, Special Issue: In honor of Friedrich Hirzebruch., 873–914. MR2532709 (2010g:57026) Zbl 1196.57018
- [Kreck1984] M. Kreck, Manifolds with unique differentiable structure, Topology 23 (1984), no.2, 219–232. MR744852 (85j:57051) Zbl 0547.57025
- [Kühl&Macko&Mole2011] P. Kuehl, T. Macko and A. Mole, The total surgery obstruction revisited, (2011). Available at the arXiv:1104.5092.
- [Levine1983] J. P. Levine, Lectures on groups of homotopy spheres, Algebraic and geometric topology (New Brunswick, N.J., 1983), Lecture Notes in Math., 1126 (1983), 62–95. MR802786 (87i:57031) Zbl 0576.57028
- [Lück&Reich2006] W. Lück and H. Reich, Detecting
 -theory by cyclic homology, Proc. London Math. Soc. (3) 93 (2006), no.3, 593–634. MR2266961 (2007h:19008) Zbl 1116.19002
-theory by cyclic homology, Proc. London Math. Soc. (3) 93 (2006), no.3, 593–634. MR2266961 (2007h:19008) Zbl 1116.19002
- [Lück1987] W. Lück, The geometric finiteness obstruction, Proc. London Math. Soc. (3) 54 (1987), no.2, 367–384. MR872812 (88i:57007) Zbl 0626.57011
- [Lück1989] W. Lück, Transformation groups and algebraic
 -theory, LNM, 1408, Springer-Verlag, 1989. MR1027600 (91g:57036) Zbl 0709.57024
-theory, LNM, 1408, Springer-Verlag, 1989. MR1027600 (91g:57036) Zbl 0709.57024
- [Lück2001] W. Lück, A basic introduction to surgery theory, 9 (2001), 1–224. Available from the author's homepage. MR1937016 (2004a:57041) Zbl 1045.57020
- [Lück2002] W. Lück,
 -invariants: theory and applications to geometry and
-invariants: theory and applications to geometry and  -theory, Springer-Verlag, Berlin, 2002. MR1926649 (2003m:58033) Zbl 1009.55001
-theory, Springer-Verlag, Berlin, 2002. MR1926649 (2003m:58033) Zbl 1009.55001
- [Lück2002a] W. Lück, Chern characters for proper equivariant homology theories and applications to
 - and
- and  -theory, J. Reine Angew. Math. 543 (2002), 193–234. MR1887884 (2003a:19003) Zbl 0987.55008
-theory, J. Reine Angew. Math. 543 (2002), 193–234. MR1887884 (2003a:19003) Zbl 0987.55008
- [Lück2002b] W. Lück, The relation between the Baum-Connes conjecture and the trace conjecture, Invent. Math. 149 (2002), no.1, 123–152. MR1914619 (2003f:19005) Zbl 1035.19003
- [Lück2005] W. Lück, Survey on classifying spaces for families of subgroups, Infinite groups: geometric, combinatorial and dynamical aspects, Progr. Math., 248, Birkhäuser, Basel (2005), 269–322. MR2195456 (2006m:55036) Zbl 1117.55013
- [Lück2008a] W. Lück, Survey on geometric group theory, Münster J. Math. 1 (2008), 73–108. MR2502495 (2010a:20092) Zbl 1197.20036
- [Madsen&Milgram1979] I. Madsen and R. J. Milgram, The classifying spaces for surgery and cobordism of manifolds, Princeton University Press, Princeton, N.J., 1979. MR548575 (81b:57014) Zbl 0446.57002
- [Madsen&Taylor&Williams1980] I. Madsen, L. R. Taylor and B. Williams, Tangential homotopy equivalences, Comment. Math. Helv. 55 (1980), no.3, 445–484. MR593058 (82f:57015) Zbl 0451.57018
- [Milnor1966] J. Milnor, Whitehead torsion, Bull. Amer. Math. Soc. 72 (1966), 358–426. MR0196736 (33 #4922) Zbl 0147.23104
- [Mislin1995] G. Mislin, Wall's finiteness obstruction, Handbook of algebraic topology, North-Holland, Amsterdam, (1995), 1259–1291. MR1361911 (97g:57029) Zbl 0870.57030
- [Novikov1970] S. P. Novikov, Algebraic construction and properties of Hermitian analogs of
 -theory over rings with involution from the viewpoint of Hamiltonian formalism. Applications to differential topology and the theory of characteristic classes. I. II, Math. USSR-Izv. 4 (1970), 257–292; ibid. 4 (1970), 479–505; translated from Izv. Akad. Nauk SSSR Ser. Mat. 34 (1970), 253–288; ibid. 34 (1970), 475. MR0292913 (45 #1994) Zbl 0216.45003 Zbl 0233.57009
-theory over rings with involution from the viewpoint of Hamiltonian formalism. Applications to differential topology and the theory of characteristic classes. I. II, Math. USSR-Izv. 4 (1970), 257–292; ibid. 4 (1970), 479–505; translated from Izv. Akad. Nauk SSSR Ser. Mat. 34 (1970), 253–288; ibid. 34 (1970), 475. MR0292913 (45 #1994) Zbl 0216.45003 Zbl 0233.57009
- [Ranicki1973] A. A. Ranicki, Algebraic
 -theory. I. Foundations, Proc. London Math. Soc. (3) 27 (1973), 101–125. MR0414661 (54 #2760a) Zbl 1256.19004
-theory. I. Foundations, Proc. London Math. Soc. (3) 27 (1973), 101–125. MR0414661 (54 #2760a) Zbl 1256.19004
- [Ranicki1980] A. Ranicki, The algebraic theory of surgery. I. Foundations, Proc. London Math. Soc. (3) 40 (1980), no.1, 87–192. MR560997 (82f:57024a) Zbl 0471.57012
- [Ranicki1980a] A. Ranicki, The algebraic theory of surgery. II. Applications to topology, Proc. London Math. Soc. (3) 40 (1980), no.2, 193–283. MR566491 (82f:57024b) Zbl 0471.57012
- [Ranicki1985] A. Ranicki, The algebraic theory of finiteness obstruction, Math. Scand. 57 (1985), no.1, 105–126. MR815431 (87d:18014) Zbl 0589.57018
- [Ranicki1985a] A. Ranicki, The algebraic theory of torsion. I. Foundations, Algebraic and geometric topology (New Brunswick, N.J., 1983), Lecture Notes in Math., 1126, Springer (1985), 199–237. MR802792 (87a:18017) Zbl 0591.18007
- [Ranicki1987] A. Ranicki, The algebraic theory of torsion. II. Products,
 -Theory 1 (1987), no.2, 115–170. MR899919 (89f:18008) Zbl 0591.18007
-Theory 1 (1987), no.2, 115–170. MR899919 (89f:18008) Zbl 0591.18007
- [Ranicki1992] A. A. Ranicki, Algebraic
 -theory and topological manifolds, Cambridge University Press, 1992. MR1211640 (94i:57051) Zbl 0767.57002
-theory and topological manifolds, Cambridge University Press, 1992. MR1211640 (94i:57051) Zbl 0767.57002
- [Ranicki2002] A. Ranicki, Algebraic and geometric surgery, The Clarendon Press Oxford University Press, Oxford, 2002. MR2061749 (2005e:57075) Zbl 1003.57001
- [Ranicki2002a] A. Ranicki, Foundations of algebraic surgery, Topology of high-dimensional manifolds, No. 1, 2 (Trieste, 2001), Abdus Salam Int. Cent. Theoret. Phys., Trieste (2002), 491–514. MR1937022 (2004a:57042) Zbl 0471.57010
- [Rosenberg1994] J. Rosenberg, Algebraic
 -theory and its applications, Graduate Texts in Mathematics, 147, Springer-Verlag, 1994. MR1282290 (95e:19001) Zbl 0801.19001
-theory and its applications, Graduate Texts in Mathematics, 147, Springer-Verlag, 1994. MR1282290 (95e:19001) Zbl 0801.19001
- [Schultz1987] R. Schultz, Homology spheres as stationary sets of circle actions, Mich. Math. J. 34 (1987), 183-200. MR0894870 (88h:57038) Zbl 0698.57012
- [Switzer2002] R. M. Switzer, Algebraic topology - homotopy and homology, Classics in Mathematics. Reprint of the 1975 original, Springer-Verlag, 2002. MR1886843 Zbl 0629.55001
- [Wall1963] C. T. C. Wall, Quadratic forms on finite groups, and related topics, Topology 2 (1963), 281–298. MR0156890 (28 #133) Zbl 0215.39903
- [Wall1965a] C. T. C. Wall, Finiteness conditions for
 -complexes, Ann. of Math. (2) 81 (1965), 56–69. MR0171284 (30 #1515) Zbl 0152.21902
-complexes, Ann. of Math. (2) 81 (1965), 56–69. MR0171284 (30 #1515) Zbl 0152.21902
- [Wall1966b] C. T. C. Wall, Finiteness conditions for
 complexes. II, Proc. Roy. Soc. Ser. A 295 (1966), 129–139. MR0211402 (35 #2283)Zbl 0152.21902
complexes. II, Proc. Roy. Soc. Ser. A 295 (1966), 129–139. MR0211402 (35 #2283)Zbl 0152.21902
- [Wall1970b] C. T. C. Wall, Surgery on compact manifolds, Academic Press, London, 1970. MR0431216 (55 #4217) Zbl 0935.57003