Structure set (Ex)
From Manifold Atlas
The exercise has two parts depending on whether we are talking about homotopy equivalences or simple homotopy equivalence. Both proofs are rather careful reading of definitions and share the same idea.
- Let
![\mathcal{S}(M) = \{[(N,f) \text{ such that } f\colon N\simeq M]\}](/images/math/9/6/e/96e323175be23d3ad52060f365606821.png) be the structure set of a closed manifold and let
be the structure set of a closed manifold and let 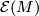 be the group of homotopy self-equivalences of
be the group of homotopy self-equivalences of  . Note that
. Note that 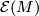 acts on
acts on 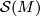 by post composition: Show that the set
by post composition: Show that the set![\displaystyle \begin{array}{rcl} \mathcal{S}(M) \times \mathcal{E}(M) & \to & \mathcal{S}(M),\\ ([f:N\to M],[g]) &\mapsto& [g\circ f: N\to M].\end{array}](/images/math/6/9/2/6922b84f7fc78f50d4a99628008d9f22.png)
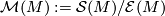 is in bijection with the set of h-cobordism classes of manifolds homotopy equivalent to
is in bijection with the set of h-cobordism classes of manifolds homotopy equivalent to  .
.
- Let
![\mathcal{S}^s(M) = \{[(N,f) \text{ such that } f\colon N\simeq_s M]\}](/images/math/b/8/d/b8d3782ba5cdbb5cea4d0a09d2a7ae54.png) be the simple structure set of a closed manifold and let
be the simple structure set of a closed manifold and let 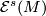 be the group of simple homotopy self-equivalences of
be the group of simple homotopy self-equivalences of  . Note that
. Note that 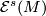 acts on
acts on 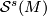 by post composition: Show that the set
by post composition: Show that the set![\displaystyle \begin{array}{rcl} \mathcal{S}^s(M) \times \mathcal{E}^s(M) & \to & \mathcal{S}^s(M),\\ ([f:N\to M],[g]) &\mapsto & [g\circ f: N\to M].\end{array}](/images/math/9/c/1/9c1e9fb90df8eb38d3c44d969517ab2a.png)
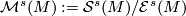 is in bijection with the set of diffeomorphism classes of manifolds homotopy equivalent to
is in bijection with the set of diffeomorphism classes of manifolds homotopy equivalent to  .
.