Whitehead torsion (Ex)
From Manifold Atlas
Show that ![1 - t - t^{-1} \in \Zz[\Zz/5]](/images/math/2/8/5/28577726cd93bb2c4c5750b1686c1454.png) for
for 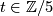 the generator is a unit and hence
defines an element
the generator is a unit and hence
defines an element 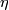 in
in 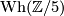 . Prove that we obtain a well-defined map
. Prove that we obtain a well-defined map
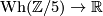
by sending the class represented by the ![\Zz[\Zz/5]](/images/math/c/4/7/c47437a1f5e6e690b9e440d2eaac1f1a.png) -automorphism
-automorphism ![f \colon \Zz[\Zz/5]^n \to \Zz[\Zz/5]^n](/images/math/a/a/4/aa45aa847ac82be4bf86bead28b0d0af.png) to
to  , where
, where 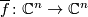 is the
is the 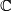 -linear map
-linear map
![\displaystyle f \otimes_{\Zz[\Zz/5]} \id_{\Cc} \colon \Zz[\Zz/5]^n \otimes_{\Zz[\Zz/5]} \Cc \to \Zz[\Zz/5]^n \otimes_{\Zz[\Zz/5]} \Cc](/images/math/2/1/5/215a48a8f87766a233c0ac9407a69cc7.png)
with respect to the 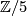 -action on
-action on 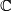 given by multiplication with
given by multiplication with 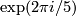 .
Finally show that
.
Finally show that 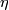 generates an infinite cyclic subgroup in
generates an infinite cyclic subgroup in 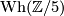 .
.
This is a detailed version of [Milnor1966, Example 6.6] and [Kreck&Lück2005, Ex 5.4].