Homology braid II (Ex)
1) Let 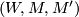 be a cobordism of
be a cobordism of 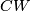 -complexes. Show that the commuting diagram
-complexes. Show that the commuting diagram
![\displaystyle \xymatrix{M^\prime \ar[dr] \ar[rr] && W/M \\ & W \ar[ur] & }](/images/math/c/c/5/cc50854c00a1432e44166f7b4afcb2a3.png)
induces a commutative diagram of cofibre sequences
![\displaystyle \xymatrix{ M^\prime \ar[dr] \ar@/^2pc/[rr] && W/M \ar[dr] \ar@/^2pc/[rr] && \Sigma M \\ & W \ar[dr] \ar[ur] && W/M\cup M^\prime \ar[dr] \ar[ur] && \\ M \ar[ur] \ar@/_2pc/[rr] && W/M^\prime \ar[ur] \ar@/_2pc/[rr] && \Sigma M^\prime \\ }](/images/math/3/a/9/3a9cec9f550f90a4b00ca75f66c7a324.png)
and hence a commutative braid of long exact sequences in Homology
![\displaystyle \xymatrix{ H_*(M^\prime) \ar[dr] \ar@/^2pc/[rr] && H_*(W/M) \ar[dr] \ar@/^2pc/[rr] && H_{*-1}(M) \\ & H_*(W) \ar[dr] \ar[ur] && H_*(W/M\cup M^\prime) \ar[dr] \ar[ur] && \\ H_*(M) \ar[ur] \ar@/_2pc/[rr] && H_*(W/M^\prime) \ar[ur] \ar@/_2pc/[rr] && H_{*-1}(M^\prime) \\ }](/images/math/d/2/f/d2f7716cb2de025aa6d7ceef9430b79b.png)
2) Now let  be a closed
be a closed 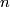 -dimensional manifold and
-dimensional manifold and 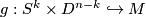 a framed embedding. Denote by
a framed embedding. Denote by 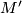 the effect of a surgery on
the effect of a surgery on  and by
and by 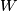 the corresponding trace, i.e.
the corresponding trace, i.e.
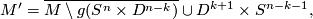
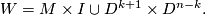
Denote by 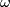 the orientation character of
the orientation character of  , i.e.
, i.e. 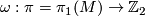 and by
and by 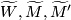 the corresponding universal covers. Write
the corresponding universal covers. Write 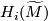 etc. for the homology with
etc. for the homology with ![\mathbb{Z}[\pi]](/images/math/5/3/9/5393263cfc1a4eb9ce95b62982af4354.png) -coefficients.
-coefficients.
Show that there exists a commutative braid of exact sequences
![\displaystyle \def\curv{1.5pc}% Adjust the curvature of the curved arrows here \xymatrix@!R@!C@!0@R=2.5pc@C=4pc{% Adjust the spacing here H_{i+1}(\widetilde{W},\widetilde{M}) \ar[dr] \ar@/u\curv/[rr] && H_{i}(\widetilde{M}) \ar[dr] \ar@/u\curv/[rr] && H_{i}(\widetilde{W},\widetilde{M}') \\ & H_{i+1}(\widetilde{W},\widetilde{M}\cup\widetilde{M}') \ar[dr] \ar[ur] && H_{i}(\widetilde{W}) \ar[dr] \ar[ur] \\ H_{i+1}(\widetilde{W},\widetilde{M}') \ar[ur] \ar@/d\curv/[rr] && H_{i}(\widetilde{M}') \ar[ur] \ar@/d\curv/[rr] && H_{i}(\widetilde{W},\widetilde{M}) }](/images/math/0/a/c/0ac9ff3212a207c04f3a508a8ca3d33b.png)
3) Show that the relative homology modules are given by
![\displaystyle H_{i}(\widetilde{W},\widetilde{M})=\left\{\begin{array}{ll} \mathbb{Z}[\pi] & \textrm{if } i=k+1\\ 0 & \textrm{otherwise}\\ \end{array}\right.](/images/math/e/8/d/e8d19e3beaabd10875a353c3e092aa59.png)
![\displaystyle H_{i}(\widetilde{W},\widetilde{M}')=\left\{\begin{array}{ll} \mathbb{Z}[\pi] & \textrm{if } i=n-k\\ 0 & \textrm{otherwise}\\ \end{array}\right.](/images/math/4/e/9/4e94c69a1a666a2a0ca4ccabfb9874f9.png)
4)Assume 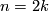 and look at the top bit of the braid
and look at the top bit of the braid
![\displaystyle \def\curv{1.5pc}% Adjust the curvature of the curved arrows here \xymatrix@!R@!C@!0@R=2.5pc@C=4pc{% Adjust the spacing here H_{k+1}(\widetilde{W},\widetilde{M}) \ar@/u\curv/[rr]^{\alpha} && H_{k}(\widetilde{M}) \ar@/u\curv/[rr]^{\beta} && H_{k}(\widetilde{W},\widetilde{M}') }](/images/math/2/7/5/275314403ddad07c18535bfb6e0827bf.png)
Let  be the Hurewicz image of
be the Hurewicz image of ![[g|]](/images/math/d/1/f/d1f9a93e2e2c0f0312d1e41594be235a.png) with
with 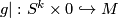 being the restriction of the framed embedding we do the surgery on.
being the restriction of the framed embedding we do the surgery on.
a) Verify that 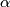 is (geometrically) given by sending the generator 1 to
is (geometrically) given by sending the generator 1 to  .
.
b) Verify that 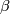 is (geometrically) given by sending a class
is (geometrically) given by sending a class 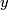 to its (equivariant) homology intersection with
to its (equivariant) homology intersection with  ,
, ![\lambda(x,y)\in\mathbb{Z}[\pi]](/images/math/1/c/3/1c30f65fde26493de4f98dd72befc3af.png) .
.