Even dimensional surgery obstruction (Ex)
From Manifold Atlas
This question is intended to illustrate the importance of the normal map in defining the even-dimensional surgery obstruction.
- Show that any closed, orientable
 -manifold
-manifold 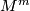 , possesses a degree 1 map
, possesses a degree 1 map 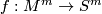 .
.
- For
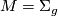 , find all degree 1 normal maps
, find all degree 1 normal maps 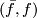 that cover
that cover 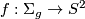 .
.
- For each of the
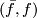 , calculate the surgery obstruction
, calculate the surgery obstruction 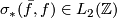 . If this vanishes, write down an explicit surgery on
. If this vanishes, write down an explicit surgery on 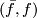 that describes a cobordism between
that describes a cobordism between 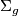 and
and 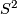 .
.
Note if there is surgery obstruction that even though we know 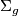 is cobordant to
is cobordant to 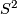 , the wrong normal map in the surgery programme will not find this cobordism.
, the wrong normal map in the surgery programme will not find this cobordism.