Template:Lück2001
From Manifold Atlas
W. Lück, A basic introduction to surgery theory, 9 (2001), 1–224. Available from the author's homepage. MR1937016 (2004a:57041) Zbl 1045.57020
Comments and corrections for this work follow organised by chapter.
Contents |
[edit] 1 Chapter 1
[edit] 2 Chapter 2
[edit] 3 Chapter 3
page 57:
- In equation (3.22) one should mention that
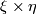 is a bundle over the product
is a bundle over the product 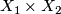 .
.
- Typos at the bottom: write
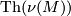 instead of
instead of 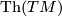 three times.
three times.
- Typo in line 11: write
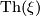 instead of
instead of 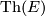 .
.
page 58:
- typo in line 8 from the bottom: write
 :
: 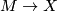 instead of
instead of  :
: 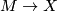 .
.
- In the proof of Theorem 3.26:
 is a CW complex, not a manifold. Why is
is a CW complex, not a manifold. Why is 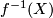 a manifold? What is the exact definition of transversality here?
a manifold? What is the exact definition of transversality here?
page 59:
- The word 'homomorphism' in line 3 is confusing, since the group structure on
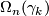 is not clear.
is not clear.
- Typo in line 9: write
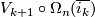 instead of
instead of 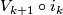 .
.
- Typo in the definition of
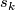 : write
: write 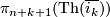 instead of
instead of 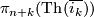 .
.
page 60:
- Typo in line 3: write
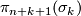 instead of
instead of 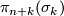 .
.
page 61:
- Typo in line 1: write
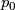 :
: 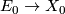 instead of
instead of 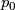 :
: 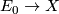 .
.
- Typo in line 1: write
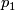 :
: 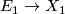 instead of
instead of 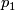 :
: 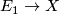 .
.
page 62:
- Typo in the assertion of Theorem 3.38: write
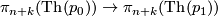 instead of
instead of 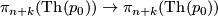 .
.
page 64:
- Typo in Lemma 3.40: write
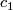 :
: 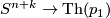 instead of
instead of 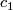 :
: 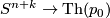 .
.
- Lemma 3.40 uses the notion of degree for maps between arbitrary Poincare complexes. It would be helpful to provide a general definition of degree in the lecture notes before this lemma.
page 65:
- Typo in line 3: write
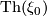 instead of
instead of 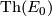 .
.
- In the three lines after 'One can arrange that these stabilization maps...' it would be useful to have a more precise explanation, why one should use cofibrations.
- Typo in line 13 from the bottom: write Spivak normal
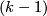 -fibration instead of Spivak normal
-fibration instead of Spivak normal 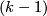 -bundle.
-bundle.
- Remark 3.44:
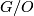 is used here but the definition of
is used here but the definition of 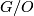 is after the Remark. It is better to give the definition of
is after the Remark. It is better to give the definition of 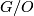 already here. Also it does not become clear what
already here. Also it does not become clear what 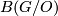 is.
is.
page 67:
- In Definition 3.46: If two vector bundles
 and
and 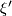 are isomorphic but not equal, the corresponding normal
are isomorphic but not equal, the corresponding normal  -maps should nevertheless be identified. However in this definition only equal vector bundles are identified. See Part 1 on the following discussion page for some suggestions on this definition.
-maps should nevertheless be identified. However in this definition only equal vector bundles are identified. See Part 1 on the following discussion page for some suggestions on this definition.
- After Definition 3.46 the notion of degree of a map between Poincare pairs is used. It would be helpful to provide a general definition in the lecture notes before.
- One would like to have more details of the proof of Theorem 3.48. This theorem is an important step and thus should be treated more precisely.
page 68:
- In Definition 3.50 one should consider closed manifolds, not closed oriented manifolds. Also there are some typos in the definition of bordism after Definition 3.50. See Part 2 on the following discussion page for some suggestions on this definition.
page 69:
- In line 3 one should consider closed manifolds, not closed oriented manifolds.
[edit] 4 Chapter 4
Example 4.20: the surgery is performed on the zero element in 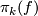 not in
not in 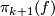 .
.