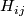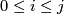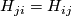Formal group laws and genera
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 09:29, 1 April 2011 and the changes since publication. |
Contents |
[edit] 1 Introduction
The theory of formal group laws, which originally appeared in algebraic geometry, was brought into bordism theory in the pioneering work [Novikov1967]. The applications of formal group laws in algebraic topology are closely connected with Hirzebruch genera [Hirzebruch1966], which are important invariants of bordism classes of manifolds.
[edit] 2 Elements of the theory of formal group laws
Let  be a commutative ring with unit.
be a commutative ring with unit.
A formal power series ![F(u,v)\in R[[u,v]]](/images/math/7/4/f/74f4f62ad66dd8d43f3631de0acc5087.png) is called a
(commutative one-dimensional) formal group law over
is called a
(commutative one-dimensional) formal group law over  if
it satisfies the following equations:
if
it satisfies the following equations:
-
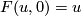 ,
, 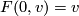 ;
;
-
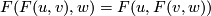 ;
;
-
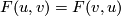 .
.
The original example of a formal group law over a field 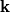 is
provided by the expansion near the unit of the multiplication map
is
provided by the expansion near the unit of the multiplication map
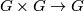 in a one-dimensional algebraic group over
in a one-dimensional algebraic group over 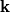 .
This also explains the terminology.
.
This also explains the terminology.
A formal group law  over
over  is called linearisable if
there exists a coordinate change
is called linearisable if
there exists a coordinate change ![u\mapsto g_F(u)=u+\sum_{i>1}g_iu^i\in R[[u]]](/images/math/9/e/8/9e894f9173595d044ca33abdc136b98e.png) such that
such that
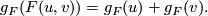
Note that every formal group law over  determines a formal
group law over
determines a formal
group law over  .
.
Theorem 2.1.
Every formal group law  is linearisable over
is linearisable over  .
.
Proof. Consider the series 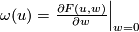 . Then
. Then
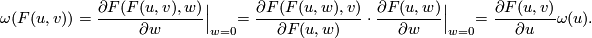
We therefore have
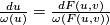 . Set
. Set
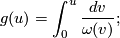
then 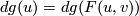 . This implies that
. This implies that 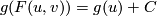 .
Since
.
Since 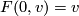 and
and 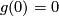 , we get
, we get 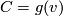 . Thus,
. Thus,
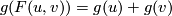 .
. 
A series 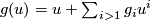 satisfying the equation
satisfying the equation 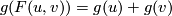 is called
a logarithm of the formal group law
is called
a logarithm of the formal group law  ; the above Theorem
shows that a formal group law over
; the above Theorem
shows that a formal group law over  always has a logarithm. Its functional inverse series
always has a logarithm. Its functional inverse series
![f(t)\in R\otimes\mathbb Q[[t]]](/images/math/d/8/d/d8df1357c59114c6756e554a41d3d2cb.png) is called an exponential of
the formal group law, so that we have
is called an exponential of
the formal group law, so that we have 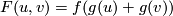 over
over  . If
. If  does not have torsion (i.e.
does not have torsion (i.e. 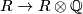 is monic), the latter formula shows that a formal group law (as a series with coefficients in
is monic), the latter formula shows that a formal group law (as a series with coefficients in  ) is fully
determined by its logarithm (which is a series with coefficients in
) is fully
determined by its logarithm (which is a series with coefficients in  ).
).
Let 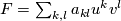 be a formal group law over a ring
be a formal group law over a ring
 and
and 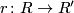 a ring homomorphism. Denote by
a ring homomorphism. Denote by 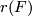 the formal series
the formal series ![\sum_{k,l}r(a_{kl})u^kv^l\in R'[[u,v]]](/images/math/7/9/f/79f6c5bbdc00bf4b92d352b3ad689c32.png) ; then
; then
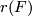 is a formal group law over
is a formal group law over 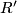 .
.
A formal group law 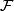 over a ring
over a ring  is universal if
for any formal group law
is universal if
for any formal group law  over any ring
over any ring  there exists a
unique homomorphism
there exists a
unique homomorphism 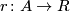 such that
such that 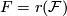 .
.
Proposition 2.2.
Assume that a universal formal group law 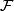 over
over  exists.
Then
exists.
Then
- The ring
 is multiplicatively generated by the coefficients of the series
is multiplicatively generated by the coefficients of the series 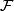 ;
;
- The universal formal group law is unique: if
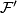 is another universal formal group law over
is another universal formal group law over 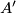 , then there is an isomorphism
, then there is an isomorphism 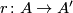 such that
such that 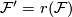 .
.
Proof. To prove the first statement, denote by 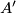 the subring in
the subring in  generated by the coefficients of
generated by the coefficients of 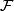 . Then there is a
monomorphism
. Then there is a
monomorphism 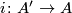 satisfying
satisfying 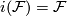 . On the
other hand, by universality there exists a homomorphism
. On the
other hand, by universality there exists a homomorphism 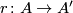 satisfying
satisfying 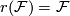 . It follows that
. It follows that 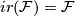 .
This implies that
.
This implies that 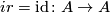 by the uniqueness
requirement in the definition of
by the uniqueness
requirement in the definition of 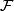 . Thus
. Thus 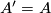 . The second
statement is proved similarly.
. The second
statement is proved similarly. 
Theorem 2.3 ([Lazard1955]).
The universal formal group law 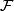 exists, and its coefficient
ring
exists, and its coefficient
ring  is isomorphic to the polynomial ring
is isomorphic to the polynomial ring ![\mathbb Z[a_1,a_2,\ldots]](/images/math/8/2/c/82c9310fe354b92a2a7693849d745f6e.png) on an infinite number of generators.
on an infinite number of generators.
[edit] 3 Formal group law of geometric cobordisms
The applications of formal group laws in cobordism theory build upon the following basic example.
Let  be a cell complex and
be a cell complex and 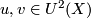 two geometric cobordisms
corresponding to elements
two geometric cobordisms
corresponding to elements 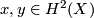 respectively. Denote by
respectively. Denote by
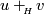 the geometric cobordism corresponding to the
cohomology class
the geometric cobordism corresponding to the
cohomology class 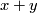 .
.
Proposition 3.1.
The following relation holds in 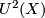 :
:
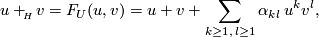
where the coefficients 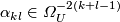 do
not depend on
do
not depend on  . The series
. The series 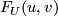 is a formal group law over the complex bordism
ring
is a formal group law over the complex bordism
ring 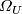 .
.
The series 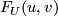 is called the formal group law of
geometric cobordisms; nowadays it is also usually referred to as the "formal group law of complex cobordism".
is called the formal group law of
geometric cobordisms; nowadays it is also usually referred to as the "formal group law of complex cobordism".
The geometric cobordism 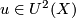 is the
first Conner-Floyd Chern class of the complex line bundle
is the
first Conner-Floyd Chern class of the complex line bundle
 over
over  obtained by pulling back the canonical bundle along
the map
obtained by pulling back the canonical bundle along
the map 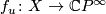 . It follows that the formal
group law of geometric cobordisms gives an expression of the first
class
. It follows that the formal
group law of geometric cobordisms gives an expression of the first
class 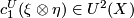 of the tensor product of
two complex line bundles over
of the tensor product of
two complex line bundles over  in terms of the classes
in terms of the classes
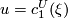 and
and 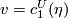 of the factors:
of the factors:
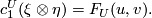
The coefficients of the formal group law of geometric cobordisms and its logarithm may be described geometrically by the following results.
Theorem 3.3 (Mishchenko, see [Novikov1967]). The logarithm of the formal group law of geometric cobordisms is given by the series
![\displaystyle g_U(u)=u+\sum_{k\ge1}\frac{[\mathbb C P^k]}{k+1}u^{k+1} \in\varOmega_U\otimes\mathbb Q[[u]].](/images/math/d/1/8/d1888212ed721161cffa98401dafec84.png)
Using these calculations the following most important property of the formal group law  can be easily established:
can be easily established:
Theorem 3.4 ([Quillen1969]).
The formal group law  of geometric cobordisms is universal.
of geometric cobordisms is universal.
The earliest applications of formal group laws in cobordism concerned finite group actions on manifolds, or "differentiable periodic maps", see [Novikov1967], [Buchstaber&Novikov1971], [Buchstaber&Mishchenko&Novikov1971]. For instance, a theorem of [Novikov1967] describes the complex cobordism ring of the classifying space of the group 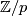 as
as
![\displaystyle U^*(B\mathbb Z/p)\cong\varOmega_U[[u]]/[u]_p,](/images/math/b/d/7/bd7da689ff14861c5d795b6b619a1156.png)
where ![\varOmega_U[[u]]](/images/math/3/f/e/3feba2059a53a5fbe5610295beed27ae.png) denotes the ring of power series in one generator
denotes the ring of power series in one generator  of degree 2 with coefficients in
of degree 2 with coefficients in 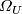 , and
, and ![[u]_p](/images/math/a/c/5/ac5fed2f54cfbb3ddc12cfb9fd265a2b.png) denotes the
denotes the  th power in the formal group law of geometric cobordisms. This result extended and unified many earlier calculations of bordism with
th power in the formal group law of geometric cobordisms. This result extended and unified many earlier calculations of bordism with 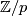 -actions from [Conner&Floyd1964].
-actions from [Conner&Floyd1964].
The universality of the formal group law of geometric cobordisms has important consequences for the stable homotopy theory: it implies that complex bordism is the universal complex oriented cohomology theory.
[edit] 4 Hirzebruch genera
Every homomorphism 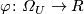 from the
complex cobordism ring to a commutative ring
from the
complex cobordism ring to a commutative ring  with unit can be
regarded as a multiplicative characteristic of manifolds which is
an invariant of cobordism classes. Such a homomorphism is called
a (complex)
with unit can be
regarded as a multiplicative characteristic of manifolds which is
an invariant of cobordism classes. Such a homomorphism is called
a (complex)  -genus. (The term "multiplicative genus" is also used, to emphasise that such a genus is a
ring homomorphism; in classical algebraic geometry, there are instances of genera which are not
multiplicative.)
-genus. (The term "multiplicative genus" is also used, to emphasise that such a genus is a
ring homomorphism; in classical algebraic geometry, there are instances of genera which are not
multiplicative.)
Assume that the ring  does not have additive torsion. Then
every
does not have additive torsion. Then
every  -genus
-genus 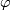 is fully determined by the corresponding
homomorphism
is fully determined by the corresponding
homomorphism 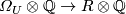 , which we shall
also denote by
, which we shall
also denote by 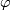 . The following famous construction of [Hirzebruch1966] allows us to describe homomorphisms
. The following famous construction of [Hirzebruch1966] allows us to describe homomorphisms
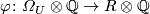 by means of
universal
by means of
universal  -valued characteristic classes of special type.
-valued characteristic classes of special type.
[edit] 4.1 Construction
Let 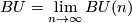 . Then
. Then 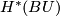 is
isomorphic to the graded ring of formal power series
is
isomorphic to the graded ring of formal power series
![\mathbb Z[[c_1,c_2,\ldots]]](/images/math/d/b/d/dbd73bb4b784d736b238bf817a071f35.png) in universal Chern classes,
in universal Chern classes, 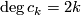 .
The set of Chern characteristic numbers of a manifold
.
The set of Chern characteristic numbers of a manifold  defines
an element in
defines
an element in 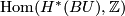 , which in fact belongs to the
subgroup
, which in fact belongs to the
subgroup 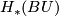 in the latter group. We therefore obtain a
group homomorphism
in the latter group. We therefore obtain a
group homomorphism
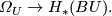
Since the multiplication in the ring 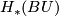 is obtained from
the maps
is obtained from
the maps 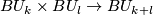 corresponding to the
Whitney sum of vector bundles, and the Chern classes have the
appropriate multiplicative property,
corresponding to the
Whitney sum of vector bundles, and the Chern classes have the
appropriate multiplicative property, 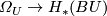 is a
ring homomorphism.
is a
ring homomorphism.
Part 2 of the structure theorem for complex bordism says that
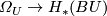 is a monomorphism, and Part 1 of the same theorem says that the corresponding
is a monomorphism, and Part 1 of the same theorem says that the corresponding 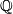 -map
-map
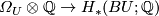 is an isomorphism. It follows
that every homomorphism
is an isomorphism. It follows
that every homomorphism 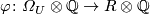 can be interpreted as an element of
can be interpreted as an element of
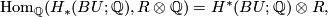
or as a sequence of homogeneous polynomials
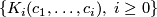 ,
, 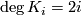 . This sequence of
polynomials cannot be chosen arbitrarily; the fact that
. This sequence of
polynomials cannot be chosen arbitrarily; the fact that 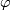 is a ring homomorphism imposes certain conditions. These
conditions may be described as follows: an identity
is a ring homomorphism imposes certain conditions. These
conditions may be described as follows: an identity
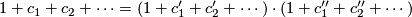
implies the identity
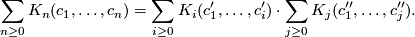
A sequence of homogeneous polynomials
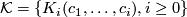 with
with 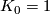 satisfying these
identities is called a multiplicative Hirzebruch sequence.
satisfying these
identities is called a multiplicative Hirzebruch sequence.
Proposition 4.1.
A multiplicative sequence 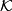 is completely determined by the series
is completely determined by the series
![\displaystyle Q(x)=1+q_1x+q_2x^2+\cdots\in R\otimes\Qq[[x]],](/images/math/0/c/7/0c7d1e2f99757bbb07ff37542beecf95.png)
where 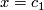 , and
, and 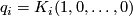 ; moreover, every series
; moreover, every series 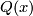 as above determines a multiplicative sequence.
as above determines a multiplicative sequence.
Proof. Indeed, by considering the identity
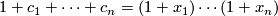
we obtain that
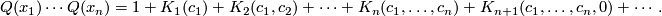

Along with the series 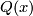 it is convenient to consider the
series
it is convenient to consider the
series ![f(x)\in R\otimes\mathbb Q[[x]]](/images/math/4/c/2/4c288a447d7068398ad73cece29a201d.png) with leading term
with leading term  given by
the identity
given by
the identity
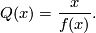
It follows that ring homomorphisms
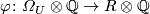 are in
one-to-one correspondence with series
are in
one-to-one correspondence with series ![f(x)\in R\otimes\mathbb Q[[x]]](/images/math/4/c/2/4c288a447d7068398ad73cece29a201d.png) with leading term
with leading term  .
Under this correspondence, the value of
.
Under this correspondence, the value of 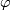 on an
on an
 -dimensional bordism class
-dimensional bordism class ![[M]\in\varOmega_U](/images/math/7/3/0/7303861967fc100e3ad678181b280ba1.png) is given
by
is given
by
![\displaystyle \varphi[M]=\Bigl(\prod^n_{i=1}\frac{x_i}{f(x_i)}, \langle M\rangle\Bigr)](/images/math/2/3/4/234d2f4052f422a1b5dd5ed93933832a.png)
where one needs to plug in the Chern classes  for the elementary symmetric functions
in
for the elementary symmetric functions
in  and then calculate the value of the resulting characteristic class on the fundamental class
and then calculate the value of the resulting characteristic class on the fundamental class 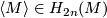 .
.
The homomorphism 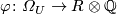 given by
the formula above is called the Hirzebruch genus
associated to the series
given by
the formula above is called the Hirzebruch genus
associated to the series ![f(x)=x+\cdots\in R\otimes\mathbb Q[[x]]](/images/math/0/e/7/0e71db5e3c8cfd0a4a2c52505e0d0217.png) . Thus, there is a one-two-one correspondence
between series
. Thus, there is a one-two-one correspondence
between series ![f(x)\in R\otimes\mathbb Q[[x]]](/images/math/4/c/2/4c288a447d7068398ad73cece29a201d.png) having leading term
having leading term  and
genera
and
genera 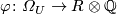 .
.
We shall also denote the
characteristic class 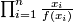 of a
complex vector bundle
of a
complex vector bundle  by
by 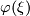 ; so that
; so that
![\varphi[M]=\varphi({\mathcal T}\!M)\langle M\rangle](/images/math/4/e/4/4e40f3d3c322bb7fd84145984f1bb6b7.png) .
.
[edit] 4.2 Connection to formal group laws
Every genus 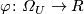 gives rise to a formal
group law
gives rise to a formal
group law 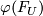 over
over  , where
, where  is
the formal group law of geometric cobordisms.
is
the formal group law of geometric cobordisms.
Theorem 4.2.
For every genus 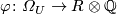 , the
exponential of the formal group law
, the
exponential of the formal group law 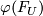 is given
by the series
is given
by the series ![f(x)\in R\otimes\mathbb Q[[x]]](/images/math/4/c/2/4c288a447d7068398ad73cece29a201d.png) corresponding to
corresponding to 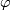 .
.
A parallel theory of genera exists for oriented manifolds. These
genera are homomorphisms 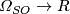 from the oriented
bordism ring, and the Hirzebruch construction expresses genera
over
from the oriented
bordism ring, and the Hirzebruch construction expresses genera
over 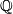 -algebras via certain Pontrjagin characteristic classes
(which replace the Chern classes).
-algebras via certain Pontrjagin characteristic classes
(which replace the Chern classes).
[edit] 4.3 Examples
We take 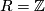 in these examples:
in these examples:
- The top Chern number
![\,c_n(\xi)[M]](/images/math/3/3/f/33f5378656551912854c52c34c626808.png) is a Hirzebruch genus, and its corresponding
is a Hirzebruch genus, and its corresponding  -series is
-series is 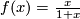 . The value of this genus on a stably complex manifold
. The value of this genus on a stably complex manifold 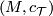 equals the Euler characteristic of
equals the Euler characteristic of  if
if 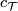 is an almost complex structure.
is an almost complex structure.
- The
 -genus
-genus ![\,L[M]](/images/math/8/c/8/8c8c56384a30fa6e03662b7cd41e2778.png) corresponds to the series
corresponds to the series 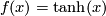 (the hyperbolic tangent). It is equal to the signature of
(the hyperbolic tangent). It is equal to the signature of  by the classical Hirzebruch formula [Hirzebruch1966].
by the classical Hirzebruch formula [Hirzebruch1966].
- The Todd genus
![\mathop{\mathrm{td}}[M]](/images/math/b/9/3/b935a5a314d732a6f03a6e0c2285e585.png) corresponds to the series
corresponds to the series 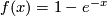 . It takes value 1 on every complex projective space
. It takes value 1 on every complex projective space 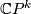 .
.
The "trivial" genus
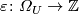 corresponding to the series
corresponding to the series
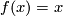 gives rise to the augmentation transformation
gives rise to the augmentation transformation
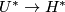 from complex cobordism to ordinary cohomology (also known as the Thom homomorphism).
More generally, for every genus
from complex cobordism to ordinary cohomology (also known as the Thom homomorphism).
More generally, for every genus 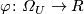 and a space
and a space  we
may set
we
may set 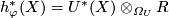 . Under
certain conditions guaranteeing the exactness of the sequences of
pairs (known as the Landweber exact functor theorem [Landweber1976])
the functor
. Under
certain conditions guaranteeing the exactness of the sequences of
pairs (known as the Landweber exact functor theorem [Landweber1976])
the functor 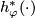 gives rise to
a complex-oriented cohomology theory with the coefficient ring
gives rise to
a complex-oriented cohomology theory with the coefficient ring
 .
.
As an example of this procedure, consider a formal indeterminate  of degree -2, and let
of degree -2, and let
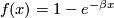 . The corresponding genus, which is also
called the Todd genus, takes values in the ring
. The corresponding genus, which is also
called the Todd genus, takes values in the ring ![\mathbb Z[\beta]](/images/math/8/6/1/86148c833fa501ebd7397cfaab3b072a.png) .
By interpreting
.
By interpreting  as the Bott element in the complex
K-group
as the Bott element in the complex
K-group 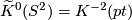 we obtain a
homomorphism
we obtain a
homomorphism 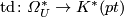 . It gives rise
to a multiplicative transformation
. It gives rise
to a multiplicative transformation 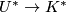 from complex
cobordism to complex K-theory introduced by Conner and
Floyd [Conner&Floyd1966]. In this paper Conner and Floyd proved that complex cobordism determines
complex K-theory by means of the isomorphism
from complex
cobordism to complex K-theory introduced by Conner and
Floyd [Conner&Floyd1966]. In this paper Conner and Floyd proved that complex cobordism determines
complex K-theory by means of the isomorphism ![K^*(X)\cong U^*(X)\otimes_{\varOmega_U}\mathbb Z[\beta]](/images/math/b/6/b/b6bb23193ed110baa8d5143094e7bfcf.png) , where the
, where the
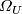 -module structure on
-module structure on ![\mathbb Z[\beta]](/images/math/8/6/1/86148c833fa501ebd7397cfaab3b072a.png) is given by the Todd genus. Their proof makes use of the Conner-Floyd Chern
classes; several proofs were given subsequently, including one which follows directly from the Landweber exact functor theorem.
is given by the Todd genus. Their proof makes use of the Conner-Floyd Chern
classes; several proofs were given subsequently, including one which follows directly from the Landweber exact functor theorem.
Another important example from the original work of Hirzebruch is
given by the 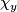 -genus. It corresponds to the series
-genus. It corresponds to the series
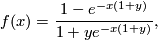
where 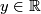 is a parameter. Setting
is a parameter. Setting 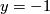 ,
, 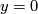 and
and 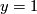 we get the top Chern number
we get the top Chern number ![c_n[M]](/images/math/e/0/4/e04930ea763cfdfed66100cc99732dec.png) , the Todd genus
, the Todd genus ![\mathop{\mathrm{td}}[M]](/images/math/b/9/3/b935a5a314d732a6f03a6e0c2285e585.png) and
the
and
the  -genus
-genus ![L[M]=\mathop{\mathrm{sign}}(M)](/images/math/7/8/9/789ed0342cc85123a4920a262542ec53.png) respectively.
respectively.
If  is a complex manifold then the value
is a complex manifold then the value ![\chi_y[M]](/images/math/c/e/5/ce5538b60b76cde4a4e1570e72b6d26c.png) can be
calculated in terms of the Euler characteristics of
Dolbeault complexes on
can be
calculated in terms of the Euler characteristics of
Dolbeault complexes on  .
.
[edit] 5 References
- [Buchstaber&Mishchenko&Novikov1971] V. M. Buhštaber, A. S. Mišcenko and S. P. Novikov, Formal groups and their role in the apparatus of algebraic topology, Uspehi Mat. Nauk 26 (1971), no.2(158), 131–154. MR0445522 (56 #3862) Zbl 0226.55007
- [Buchstaber&Novikov1971] V. M. Buhštaber and S. P. Novikov, Formal groups, power systems and Adams operators, Mat. Sb. (N.S.) 84(126) (1971), 81–118. MR0291159 (45 #253) Zbl 0239.55005
- [Buchstaber1970] V. M. Buhštaber, The Chern-Dold character in cobordisms. I, Mat. Sb. (N.S.) 83 (125) (1970), 575–595. MR0273630 (42 #8507) Zbl 0219.57027
- [Conner&Floyd1964] P. E. Conner and E. E. Floyd, Differentiable periodic maps, Academic Press Inc., Publishers, New York, 1964. MR0176478 (31 #750) Zbl 0417.57019
- [Conner&Floyd1966] P. E. Conner and E. E. Floyd, The relation of cobordism to
 -theories, Springer-Verlag, Berlin, 1966. MR0216511 (35 #7344) Zbl 0161.42802
-theories, Springer-Verlag, Berlin, 1966. MR0216511 (35 #7344) Zbl 0161.42802
- [Hirzebruch1966] F. Hirzebruch, Topological methods in algebraic geometry, Springer-Verlag, New York, 1966. MR0202713 (34 #2573) Zbl 0843.14009
- [Landweber1976] P. S. Landweber, Homological properties of comodules over
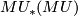 and
and 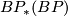 , Amer. J. Math. 98 (1976), no.3, 591–610. MR0423332 (54 #11311) Zbl 0355.55007
, Amer. J. Math. 98 (1976), no.3, 591–610. MR0423332 (54 #11311) Zbl 0355.55007
- [Lazard1955] M. Lazard, Sur les groupes de Lie formels à un paramètre, Bull. Soc. Math. France 83 (1955), 251–274. MR0073925 (17,508e) Zbl 0068.25703
- [Novikov1967] S. P. Novikov, Methods of algebraic topology from the point of view of cobordism theory, Math. USSR, Izv. 1, (1967) 827–913. MR0221509 (36 #4561) Zbl 0176.52401
- [Quillen1969] D. Quillen, On the formal group laws of unoriented and complex cobordism theory, Bull. Amer. Math. Soc. 75 (1969), 1293–1298. MR0253350 (40 #6565) Zbl 0199.26705
![\displaystyle F_U(u,v)=\frac{\sum_{i,j\ge0}[H_{ij}]u^iv^j} {\bigl(\sum_{r\ge0}[\mathbb C P^r]u^r\bigr)\bigl(\sum_{s\ge0}[\mathbb C P^s]v^s\bigr)},](/images/math/e/6/d/e6da071437c7a9dcdd2d7c12e8a337a8.png)