Oriented bordism
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
By the Pontrjagin-Thom isomorphism the oriented bordism groups 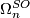 of closed oriented manifolds are isomorphic to the homotopy groups of the Thom spectrum
of closed oriented manifolds are isomorphic to the homotopy groups of the Thom spectrum  .
.
[edit] 2 Generators
-
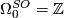 , generated by a point.
, generated by a point.
-
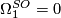 , as circles bound disks.
, as circles bound disks.
-
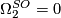 , as oriented surfaces bound handlebodies.
, as oriented surfaces bound handlebodies.
-
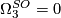 .
.
-
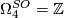 , generated by the complex projective plane
, generated by the complex projective plane 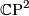 , detected by the signature.
, detected by the signature.
-
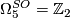 , generated by the Wu manifold
, generated by the Wu manifold 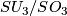 , detected by the deRham invariant.
, detected by the deRham invariant.
-
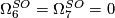 .
.
-
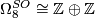 generated by
generated by 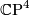 and
and 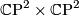 .
.
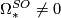 for
for 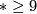 : see also [Milnor&Stasheff1974, p. 203].
: see also [Milnor&Stasheff1974, p. 203].
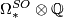 is a polynomial ring, with generators
is a polynomial ring, with generators 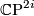 , detected by the Pontrjagin numbers.
, detected by the Pontrjagin numbers.
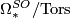 is an integral polynomial ring with generators the ``Milnor hypersurfaces``.
is an integral polynomial ring with generators the ``Milnor hypersurfaces``.
[edit] 3 Invariants
The signature of a closed oriented manifold is a fundamental bordism invariant defining a ring homomorphism
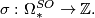
(Note that manifolds of dimension not divisible by 4 have signature zero.)
For a muli-index 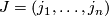 of degree
of degree 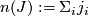 the
Pontryagin number
the
Pontryagin number 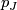 of a closed, oriented manifold
of a closed, oriented manifold  of dimension
of dimension 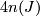 is the integer
is the integer
![\displaystyle \langle p_{j_1}(M) \cup p_{j_2}(M) \cup \dots \cup p_{j_n}(M), [M]\rangle \in \Zz](/images/math/d/5/a/d5a0ef40d8e53b9b8a4e421d1ea01adb.png)
where 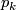 is the k-the Pontrjagin of
is the k-the Pontrjagin of  and
and ![[M]](/images/math/f/a/0/fa08c3d5d2f54260952acc8a646b5025.png) its fundamental class. The Stiefel-Whitney numbers of
its fundamental class. The Stiefel-Whitney numbers of  ,
, 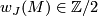 , are defined similarly using Stiefel-Whitney classes. These numbers are bordism invariants (see for example [Milnor&Stasheff1974, Theorm 4.9, Lemma 17.3]) and clearly additive. Hence we have homomorphisms
, are defined similarly using Stiefel-Whitney classes. These numbers are bordism invariants (see for example [Milnor&Stasheff1974, Theorm 4.9, Lemma 17.3]) and clearly additive. Hence we have homomorphisms
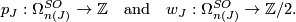
By Hirzebruch's signature theorem [Hirzebruch1953], [Hirzebruch1995, Theorem 8.2.2], there is a certain rational polynomial in the Pontrjagin classes, called the L-polynomial 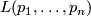 , which computes the signature of M
, which computes the signature of M
![\displaystyle \sigma(M) = \langle L_n(p_1(M), \dots , p_n(M)), [M] \rangle.](/images/math/2/4/f/24f787ebe0172284dfde21df35d8cc3d.png)
For example:
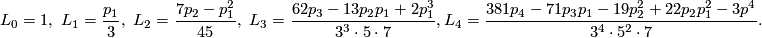
[edit] 4 Classification
Thom [Thom1954] computed 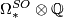 . This is equivalent to the computation of the rational (co)homology of
. This is equivalent to the computation of the rational (co)homology of 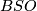 , as shown
here. The cohomology
, as shown
here. The cohomology 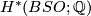 is a polynomial ring with generators the
Pontryagin classes, so that Pontryagin numbers give an additive isomorphism
is a polynomial ring with generators the
Pontryagin classes, so that Pontryagin numbers give an additive isomorphism ![\Omega_*^{SO}\otimes \Qq \cong \Qq[x_{4i}]](/images/math/c/6/d/c6d5d1c081800a5221ed7189d975c0c3.png) .
Since all products of
.
Since all products of 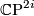 have linearly independent collections of Pontryagin numbers,
there is a ring isomorphism from
have linearly independent collections of Pontryagin numbers,
there is a ring isomorphism from 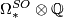 to a polynomial ring with generators
to a polynomial ring with generators 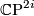 .
.
Independently Averbuch [Averbuh1959] and Milnor [Milnor1960] showed that 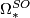 has no odd torsion. In addition, Novikov [Novikov1960] showed that
has no odd torsion. In addition, Novikov [Novikov1960] showed that 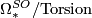 is isomorphic to a polynomial ring
is isomorphic to a polynomial ring
![\Zz[Y_4,Y_8,Y_{12}, \dots ]](/images/math/5/f/3/5f390ca8024e3b016de6c43d0913aded.png) . Here a generator
. Here a generator 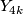 can be any
can be any  -dimensional manifold such that the Pontryagin number
-dimensional manifold such that the Pontryagin number
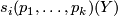 equals
equals 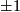 , if
, if 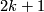 is not a prime power, or equals
is not a prime power, or equals 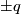 , if
, if 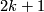 is a power of the prime
is a power of the prime  .
(Here
.
(Here 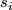 is the polynomial which expresses
is the polynomial which expresses 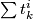 in terms of the elementary symmetric polynomials of the
in terms of the elementary symmetric polynomials of the 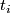 .)
.)
Wall [Wall1960], using earlier results of [Rokhlin1953], determined the structure of 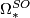 completely. In particular he proved the following theorems.
completely. In particular he proved the following theorems.
Theorem 3.1 [Wall1960, Theorem 2].
All torsion in 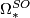 is of exponent 2.
is of exponent 2.
Theorem 3.2 [Wall1960, Corollary 1].
Two closed oriented n-manifolds  and
and  are oriented cobordant
if and only if they have the same Stiefel-Whitney and Pontryagin numbers:
are oriented cobordant
if and only if they have the same Stiefel-Whitney and Pontryagin numbers:
![\displaystyle [M_0] = [M_1] \in \Omega_n^{SO} ~~\Longleftrightarrow ~~ \ p_J(M_0) = p_J(M_1) ~~and~~ w_J(M_0) = w_J(M_1) ~~ \forall J.](/images/math/2/c/d/2cd5093093fb6f6b11878497c21a829f.png)
For the complete ring structure, we first describe the subalgebra 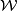 of the unoriented bordism ring
of the unoriented bordism ring 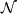 consisting of classes which contain a manifold
consisting of classes which contain a manifold  whose first Stiefel-Whitney class is the reduction of an integral class.
whose first Stiefel-Whitney class is the reduction of an integral class.
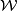 is a polynomial ring with coefficients
is a polynomial ring with coefficients 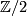 on generators
on generators 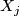 where neither
where neither  nor
nor 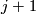 are powers of 2, together with generators
are powers of 2, together with generators 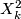 where
where  is a power of 2. These generators can be described explicitly as follows:
is a power of 2. These generators can be described explicitly as follows:
- For
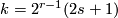 with integers
with integers  and
and  (i.e.
(i.e.  not a power of 2), the generator
not a power of 2), the generator 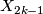 is the Dold manifold
is the Dold manifold 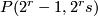 and the generator
and the generator 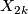 is the mapping torus of the map
is the mapping torus of the map 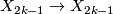 given by the reflection of
given by the reflection of 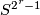 at the equator.
at the equator.
- For
 not a power of 2, the generator
not a power of 2, the generator 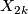 is the mapping torus of a certain involution
is the mapping torus of a certain involution 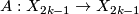 . Indeed any Dold manifold
. Indeed any Dold manifold 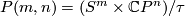 has the involution
has the involution ![A[(x_0, \ldots, x_{m-1},x_m),z] = A[(x_0, \ldots, x_{m-1},-x_m),z]](/images/math/7/9/e/79e55fc1afc57f7cd5e6945d512ad5bb.png) .
.
- For
 a power of 2, the generator
a power of 2, the generator 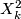 is
is 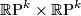 . This generator is also represented by
. This generator is also represented by 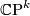 .
.
Now there is an exact sequence
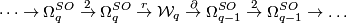
where the ring homomorphism  is induced by the forgetful map
is induced by the forgetful map 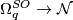 , and
, and 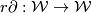 is the derivation
is the derivation 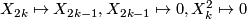 .
.
Together with the result that one can choose generators 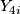 for
for 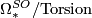 such that
such that 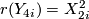 ,
this determines the ring structure of
,
this determines the ring structure of 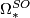 .
.
[edit] 5 References
- [Averbuh1959] B. G. Averbuh, Algebraic structure of cobordism groups, Dokl. Akad. Nauk SSSR 125 (1959), 11–14. MR0124894 (23 #A2204)
- [Hirzebruch1953] F. Hirzebruch, Über die quaternionalen projektiven Räume, S.-B. Math.-Nat. Kl. Bayer. Akad. Wiss. 1953 (1953), 301–312 (1954). MR0065155 (16,389a) Zbl 0057.15503
- [Hirzebruch1995] F. Hirzebruch, Topological methods in algebraic geometry, Springer-Verlag, Berlin, 1995. MR1335917 (96c:57002) Zbl 0843.14009
- [Milnor&Stasheff1974] J. W. Milnor and J. D. Stasheff, Characteristic classes, Princeton University Press, Princeton, N. J., 1974. MR0440554 (55 #13428) Zbl 1079.57504
- [Milnor1960] J. Milnor, On the cobordism ring
 and a complex analogue. I, Amer. J. Math. 82 (1960), 505–521. MR0119209 (22 #9975) Zbl 0095.16702
and a complex analogue. I, Amer. J. Math. 82 (1960), 505–521. MR0119209 (22 #9975) Zbl 0095.16702
- [Novikov1960] S. P. Novikov, Some problems in the topology of manifolds connected with the theory of Thom spaces, Soviet Math. Dokl. 1 (1960), 717–720. MR0121815 (22 #12545) Zbl 0094.35902
- [Rokhlin1953] V. A. Rohlin, Intrinsic homologies, Doklady Akad. Nauk SSSR (N.S.) 89 (1953), 789–792. MR0056292 (15,53b)
- [Thom1954] R. Thom, Quelques propriétés globales des variétés différentiables, Comment. Math. Helv. 28 (1954), 17–86. MR0061823 (15,890a) Zbl 0057.15502
- [Wall1960] C. T. C. Wall, Determination of the cobordism ring, Ann. of Math. (2) 72 (1960), 292–311. MR0120654 (22 #11403) Zbl 0097.38801