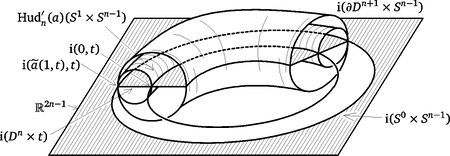
Embeddings just below the stable range: classification
| This page has been accepted for publication in the Bulletin of the Manifold Atlas. |
|
The user responsible for this page is Askopenkov. No other user may edit this page at present. |
Contents |
1 Introduction
Most of this page is intended not only for specialists in embeddings, but also for mathematician from other areas who want to apply or to learn the theory of embeddings.
Recall the Whitney-Wu Unknotting Theorem: if  is a connected manifold of dimension
is a connected manifold of dimension  , and
, and 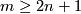 , then every two embeddings
, then every two embeddings  are isotopic [Skopenkov2016c, Theorem 3.2], [Skopenkov2006, Theorem 2.5]. In this page we summarize the situation for
are isotopic [Skopenkov2016c, Theorem 3.2], [Skopenkov2006, Theorem 2.5]. In this page we summarize the situation for 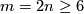 and
and  is a connected, as well as in some more general situations.
For the classification of embeddings of some disconnected manifolds see [Skopenkov2016h].
is a connected, as well as in some more general situations.
For the classification of embeddings of some disconnected manifolds see [Skopenkov2016h].
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3]. Denote
3]. Denote 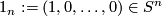 .
.
2 Classification
For the next theorem, the Whitney invariant  is defined in
is defined in  5 below.
5 below.
Theorem 2.1. Assume that  is a closed connected
is a closed connected  -manifold, and either
-manifold, and either 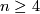 or
or  and we are in the PL category.
and we are in the PL category.
(a) If  is oriented, the Whitney invariant,
is oriented, the Whitney invariant,
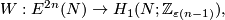
is a 1-1 correspondence.
(b) If  is non-orientable, then there is a 1-1 correspondence
is non-orientable, then there is a 1-1 correspondence

Remark 2.2 (Comments on the proof).
Part (a) is proved in [Haefliger&Hirsch1963, Theorem 2.4] in the smooth category, and in [Weber1967, Theorem 4' in  2], [Hudson1969,
2], [Hudson1969,  11], [Vrabec1977, Theorems 1.1 and 1.2] in the PL category, see also [Haefliger1962b, 1.3.e], [Haefliger1963], [Bausum1975, Theorem 43].
11], [Vrabec1977, Theorems 1.1 and 1.2] in the PL category, see also [Haefliger1962b, 1.3.e], [Haefliger1963], [Bausum1975, Theorem 43].
Part (b) is proved in [Bausum1975, Theorem 43] in the smooth category. By [Weber1967, Theorems 1 and 1' in  2], [Skopenkov1997, Theorem 1.1.c] the proof works also in the PL category.
2], [Skopenkov1997, Theorem 1.1.c] the proof works also in the PL category.
In Part (b) we replaced the kernel 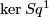 from [Bausum1975, Theorem 43] by
from [Bausum1975, Theorem 43] by 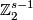 . This is possible because, as a specialist could see,
. This is possible because, as a specialist could see, 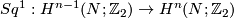 is given by multiplication with the first Stefel-Whitney class
is given by multiplication with the first Stefel-Whitney class 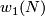 (which equals to the first Wu class
(which equals to the first Wu class 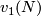 [Milnor&Stasheff1974, Theorem 11.4]). Since
[Milnor&Stasheff1974, Theorem 11.4]). Since  is non-orientable,
is non-orientable, 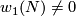 . So by Poincaré duality,
. So by Poincaré duality, 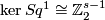 .
.
The 1-1 correspondence from (b) can presumably be defined as a (generalized) Whitney invariant, see [Vrabec1977], but the proof used 'the Haefliger-Wu invariant' whose definition can be found e.g. in [Skopenkov2006,  5].
It would be interesting to check if part (b) is equivalent to different forms of description of
5].
It would be interesting to check if part (b) is equivalent to different forms of description of 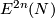 [Haefliger1962b, 1.3.e], [Haefliger1963], [Vrabec1977, Theorem 1.1].
[Haefliger1962b, 1.3.e], [Haefliger1963], [Vrabec1977, Theorem 1.1].
The classification of smooth embeddings of 3-manifolds in 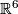 is more complicated, see Theorem 6.3 below for
is more complicated, see Theorem 6.3 below for 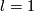 or [Skopenkov2016t].
or [Skopenkov2016t].
Concerning embeddings of connected  -manifolds in
-manifolds in 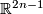 see [Yasui1984] for
see [Yasui1984] for 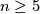 , [Skopenkov2016f] for
, [Skopenkov2016f] for 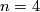 , and [Saeki1999], [Skopenkov2010], [Tonkonog2010] for manifolds with boundary.
, and [Saeki1999], [Skopenkov2010], [Tonkonog2010] for manifolds with boundary.
Theorem 2.1 is generalized to a description of 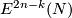 for closed
for closed  -connected
-connected  -manifolds
-manifolds  , see Theorem 6.2.
, see Theorem 6.2.
3 Hudson tori
Tex syntax errorto just
Tex syntax error.
Example 3.1. Let us construct, for any 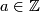 and
and  , a smooth embedding
, a smooth embedding
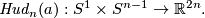
We start with the cases 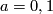 .
.
Take the standard inclusion 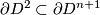 .
The 'standard embedding'
.
The 'standard embedding' 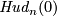 is given by the standard inclusions
is given by the standard inclusions
Tex syntax error
Tex syntax erroranalogously to
Tex syntax error, where
 means homothety with coefficient 2.
means homothety with coefficient 2.
Take the embedding 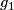 given by
given by
Tex syntax error
Tex syntax errorjoins the images of
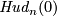 and
and 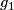 ; the interior of this segment misses the images. Let
; the interior of this segment misses the images. Let 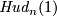 be the linked embedded connected sum of
be the linked embedded connected sum of  and
and 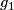 along this segment, compatible with the orientation, cf. [Avvakumov2017,
along this segment, compatible with the orientation, cf. [Avvakumov2017,  1.5]. (Here 'linked' means that the images of the embeddings are not contained in disjoint cubes, unlike for the unlinked embedded connected sum [Skopenkov2016c,
1.5]. (Here 'linked' means that the images of the embeddings are not contained in disjoint cubes, unlike for the unlinked embedded connected sum [Skopenkov2016c,  5].)
5].)
For 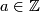 we repeat the above construction of
we repeat the above construction of 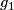 replacing
replacing 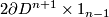 by
by
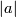 copies
copies 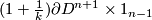 of
of  ,
, 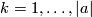 .
The copies are outside
.
The copies are outside 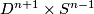 and are `parallel' to
and are `parallel' to 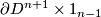 .
The copies have the standard orientation for
.
The copies have the standard orientation for 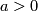 or the opposite orientation for
or the opposite orientation for  .
Then we make embedded connected sum along natural segments joining every
.
Then we make embedded connected sum along natural segments joining every  -th copy to the
-th copy to the 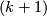 -th
copy.
We obtain an embedding
-th
copy.
We obtain an embedding 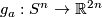 which has disjoint images with
which has disjoint images with 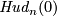 .
Let
.
Let  be the linked embedded connected sum of
be the linked embedded connected sum of 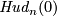 and
and 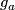 .
.
The original motivation for Hudson was that 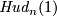 is not isotopic to
is not isotopic to 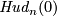 for any
for any  (this is a particular case of Proposition 3.2 below). One might guess that
(this is a particular case of Proposition 3.2 below). One might guess that  is not isotopic
to
is not isotopic
to 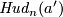 for
for 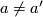 and that a
and that a  -valued invariant of
-valued invariant of 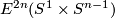 can be defined by the homotopy class of the map
can be defined by the homotopy class of the map
Tex syntax error
However, this is only true for  odd.
odd.
Proposition 3.2.
For  odd
odd  is isotopic to
is isotopic to 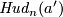 if and only if
if and only if 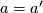 .
.
For 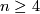 even
even  is isotopic to
is isotopic to 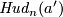 if and only if
if and only if 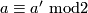 .
.
Proposition 3.2 follows by calculation of the Whitney invariant (Remark 5.3.d below) and, for  even, by Theorem 2.1.
This proposition holds with the same proof in the piecewise smooth category, whose definition is recalled in [Skopenkov2016f, Remark 1.1]). Proposition 3.2 also holds in the PL category (with an analogous construction of
even, by Theorem 2.1.
This proposition holds with the same proof in the piecewise smooth category, whose definition is recalled in [Skopenkov2016f, Remark 1.1]). Proposition 3.2 also holds in the PL category (with an analogous construction of  for the PL category).
It would be interesting to find an explicit construction of an isotopy between
for the PL category).
It would be interesting to find an explicit construction of an isotopy between 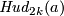 and
and
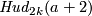 , cf. [Vrabec1977,
, cf. [Vrabec1977,  5].
Analogously,
5].
Analogously, 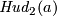 is not isotopic to
is not isotopic to 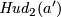 if
if 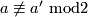 .
It would be interesting to know if the converse holds, e.g. is
.
It would be interesting to know if the converse holds, e.g. is 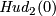 (PS or smoothly) isotopic to
(PS or smoothly) isotopic to 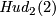 .
.
Example 3.3.
Take any 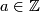 .
Take a map
.
Take a map 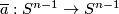 of degree
of degree  (so we can take
(so we can take 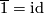 ).
Recall that
).
Recall that 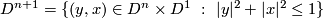 .
Define the smooth embedding
.
Define the smooth embedding 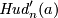 to be the composition
to be the composition
Tex syntax error
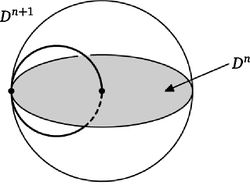
Let us present a geometric description of this embedding.
Define a map 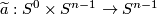 by
by 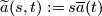 .
This map gives an embedding
.
This map gives an embedding
Tex syntax error
Tex syntax erroris the union of the graphs of the maps
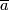 and
and 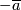 . For any
. For any 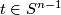 the disk
the disk Tex syntax errorintersects the image at two points lying in
Tex syntax error, i.e., at the image of an embedding
Tex syntax error. The embedding
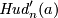 is obtained by extending the latter embeddings to embeddings
is obtained by extending the latter embeddings to embeddings Tex syntax errorfor all
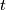 . See Figure 2.
. See Figure 2.
Remark 3.4. (a) The analogue of Proposition 3.2 for 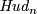 replaced to
replaced to
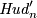 holds, with an analogous proof.
holds, with an analogous proof.
(b) The embeddings  and
and 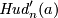 are smoothly isotopic for
are smoothly isotopic for 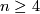 and are PS isotopic for
and are PS isotopic for  [Skopenkov2006a, commutativity of the left upper square in the Restriction Lemma 5.2], [Skopenkov2015a, Lemma 2.15.c] (see [Skopenkov2016f, Remark 1.2]).
This follows by calculation of the Whitney invariant (Remark 5.3.d below).
It would be interesting to know if they are smoothly isotopic for
[Skopenkov2006a, commutativity of the left upper square in the Restriction Lemma 5.2], [Skopenkov2015a, Lemma 2.15.c] (see [Skopenkov2016f, Remark 1.2]).
This follows by calculation of the Whitney invariant (Remark 5.3.d below).
It would be interesting to know if they are smoothly isotopic for  .
It would be interesting to know if they are piecewise smoothly isotopic for
.
It would be interesting to know if they are piecewise smoothly isotopic for  .
.
(c) For  Example 3.3 gives what we call the 'left' Hudson torus.
The 'right' Hudson torus is constructed analogously.
It is the composition of the left Hudson torus and the exchanging factors autodiffeomorphism of
Example 3.3 gives what we call the 'left' Hudson torus.
The 'right' Hudson torus is constructed analogously.
It is the composition of the left Hudson torus and the exchanging factors autodiffeomorphism of 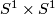 .
The right and the left Hudson tori are not isotopic by Remark 5.3.d below.
.
The right and the left Hudson tori are not isotopic by Remark 5.3.d below.
(d) Analogously one constructs the Hudson torus 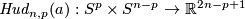 for
for 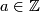 and
and 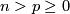 or, more generally,
or, more generally, 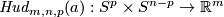 for
for 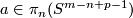 and
and 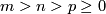 .
There are versions
.
There are versions 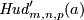 of these constructions corresponding to Definition 3.3.
For
of these constructions corresponding to Definition 3.3.
For 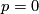 this corresponds to the Zeeman map
[Skopenkov2016h, Definition 2.2] and its composition with 'the unframed second Kirby move' [Skopenkov2015a,
this corresponds to the Zeeman map
[Skopenkov2016h, Definition 2.2] and its composition with 'the unframed second Kirby move' [Skopenkov2015a,  2.3].
It would be interesting to know if the links
2.3].
It would be interesting to know if the links 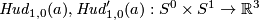 are isotopic, cf. [Skopenkov2015a, Remark 2.7.b].
These constructions can be further generalized [Skopenkov2016k].
are isotopic, cf. [Skopenkov2015a, Remark 2.7.b].
These constructions can be further generalized [Skopenkov2016k].
4 Action by linked embedded connected sum
In this section we generalize the construction of the Hudson torus 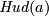 .
Let
.
Let  be a closed connected oriented
be a closed connected oriented  -manifold.
We work in the smooth category which we omit.
Apparently analogous results hold for
-manifold.
We work in the smooth category which we omit.
Apparently analogous results hold for  in the PL and PS categories (see [Skopenkov2016f, Remark 1.2]).
in the PL and PS categories (see [Skopenkov2016f, Remark 1.2]).
Example 4.1.
For any 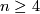 , an embedding
, an embedding 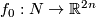 and
and 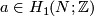 , we shall construct an embedding
, we shall construct an embedding 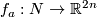 .
This embedding is said to be obtained by linked embedded connected sum of
.
This embedding is said to be obtained by linked embedded connected sum of  with an
with an  -sphere representing the `homology Alexander dual'
-sphere representing the `homology Alexander dual' 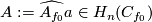 of
of  (defined in [Skopenkov2005, Alexander Duality Lemma 4.6]).
(defined in [Skopenkov2005, Alexander Duality Lemma 4.6]).
Represent  by an embedding
by an embedding 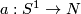 .
By definition, the class
.
By definition, the class  is represented by properly oriented
is represented by properly oriented 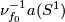 .
Since any orientable bundle over
.
Since any orientable bundle over  is trivial,
is trivial, 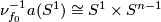 .
Take an embedding
.
Take an embedding 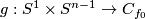 whose image is
whose image is 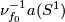 and which represents
and which represents  .
By embedded surgery on
.
By embedded surgery on 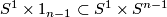 we obtain an embedding
we obtain an embedding 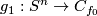 representing
representing  (see details in Proposition 4.2 below).
Define
(see details in Proposition 4.2 below).
Define 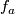 to be the linked embedded connected sum of
to be the linked embedded connected sum of  and
and 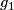 , along some arc joining their images.
, along some arc joining their images.
Proposition 4.2 (Embedded surgery).
For any  , a neighborhood
, a neighborhood  of a codimension at least 3 subpolyhedron in
of a codimension at least 3 subpolyhedron in  and an embedding
and an embedding 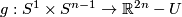 there is an embedding
there is an embedding 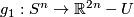 homologous to
homologous to  .
.
Proof. Take a vector field on 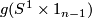 normal to
normal to 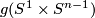 .
Extend
.
Extend 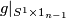 along this vector field to a map
along this vector field to a map 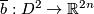 .
.
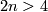 and
and  is a neighborhood
is a neighborhood  of a codimension at least 3 subpolyhedron, by general position we may assume that
of a codimension at least 3 subpolyhedron, by general position we may assume that 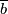 is an embedding and that
is an embedding and that Tex syntax errormisses
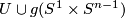 .
.
Since 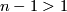 , we have
, we have 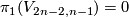 .
Hence the standard
.
Hence the standard  -framing of
-framing of 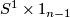 in
in 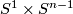 extends to an
extends to an  -framing on
-framing on 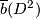 in
in  .
Thus
.
Thus 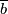 extends to an embedding
extends to an embedding

Take an embedding 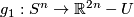 such that
such that
Tex syntax error
with proper orientation so that 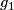 is homologous to
is homologous to  . QED
. QED
The isotopy class of the embedding 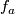 is independent of the choises in the construction.
The independence of the arc and of the maps
is independent of the choises in the construction.
The independence of the arc and of the maps 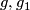 follows by
follows by  and by Proposition 4.3 below, respectively.
and by Proposition 4.3 below, respectively.
By Definition 5.1 of the Whitney invariant, 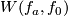 is
is  for
for  odd and
odd and 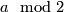 for
for 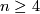 even.
Thus by Theorem 2.1.a for
even.
Thus by Theorem 2.1.a for 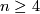 all isotopy classes of embeddings
all isotopy classes of embeddings 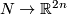 can be obtained from any chosen embedding
can be obtained from any chosen embedding  by the above construction.
by the above construction.
Proposition 4.3. For any 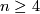 both the linked embedded connected sum and parametric connected sum (introduced in [Skopenkov2006a], [Skopenkov2015a]) define free transitive actions of
both the linked embedded connected sum and parametric connected sum (introduced in [Skopenkov2006a], [Skopenkov2015a]) define free transitive actions of 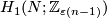 on
on 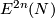 .
.
This follows by Theorem 2.1.a and by [Skopenkov2014, Remark 18.a].
5 The Whitney invariant
Let  be a closed
be a closed  -manifold.
Take an embedding
-manifold.
Take an embedding 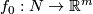 .
Fix an orientation on
.
Fix an orientation on  .
For any other embedding
.
For any other embedding 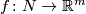 we define the Whitney invariant
we define the Whitney invariant
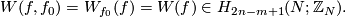
Here the coefficients 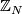 are
are  if
if  is oriented and
is oriented and  is odd, and are
is odd, and are  otherwise.
otherwise.
Tex syntax erroris defined as the homology class of the closure of the self-intersection set of a general position homotopy
 between
between  and
and  .
.
This is formalized in Definition 5.2 in the smooth category, following [Skopenkov2010], see
also [Haefliger&Hirsch1963].
The definition in the PL category is analogous [Hudson1969,  11], [Vrabec1977, p. 145],
[Skopenkov2006,
11], [Vrabec1977, p. 145],
[Skopenkov2006,  2.4 `The Whitney invariant'].
We begin by presenting a simpler definition, Definition 5.1, for a particular case.
2.4 `The Whitney invariant'].
We begin by presenting a simpler definition, Definition 5.1, for a particular case.
For Theorem 2.1 only the case 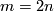 is required.
is required.
Definition 5.1.
Assume that  is
is 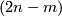 -connected and
-connected and 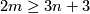 .
Then by [Haefliger&Hirsch1963, Theorem 3.1.b] restrictions of
.
Then by [Haefliger&Hirsch1963, Theorem 3.1.b] restrictions of  and
and  to
to  are isotopic, cf. [Takase2006, Lemma 2.2].
(Here is sketch of an argument. Using the Smale-Hirsch classification of immersions we obtain that restrictions of
are isotopic, cf. [Takase2006, Lemma 2.2].
(Here is sketch of an argument. Using the Smale-Hirsch classification of immersions we obtain that restrictions of  and
and  to
to  are `regular homotopic', see [Koschorke2013, Definition 2.7]. Since
are `regular homotopic', see [Koschorke2013, Definition 2.7]. Since  is
is 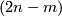 -connected,
-connected,  retracts to an
retracts to an 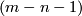 -dimensional polyhedron.
Therefore these restrictions are isotopic.)
-dimensional polyhedron.
Therefore these restrictions are isotopic.)
So we can make an isotopy of  and assume that
and assume that 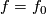 on
on  . Take a general position homotopy
. Take a general position homotopy 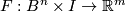 relative to
relative to 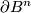 between the
restrictions of
between the
restrictions of  and
and  to
to  . Let
. Let 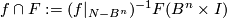 (`the intersection of this homotopy with
(`the intersection of this homotopy with 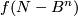 ').
').
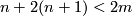 , by general position
, by general position Tex syntax erroris a compact
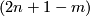 -manifold whose boundary is contained in
-manifold whose boundary is contained in 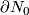 .
.
So  carries a homology class with
carries a homology class with  coefficients.
If
coefficients.
If  is odd and
is odd and  is oriented, then
is oriented, then  has a natural orientation defined below,
and so carries a homology class with
has a natural orientation defined below,
and so carries a homology class with  coefficients.
Define
coefficients.
Define 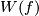 to be the homology class:
to be the homology class:
Tex syntax error
 (extendable to
(extendable to Tex syntax error) is defined (for
 odd and
odd and  is oriented) as follows (cf. Remark 7.3). For any point
is oriented) as follows (cf. Remark 7.3). For any point 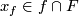 take a base
take a base 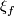 at
at 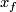 tangent to
tangent to  . Complete this base to a positive base
. Complete this base to a positive base 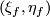 tangent to
tangent to  . Since
. Since 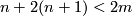 , by general position there is a unique point
, by general position there is a unique point 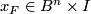 such that
such that 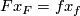 . The tangent base
. The tangent base 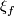 at
at 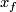 thus gives a base
thus gives a base 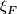 at
at 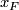 tangent to
tangent to 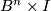 such that
such that 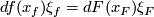 . Complete this base
. Complete this base 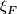 to a positive base
to a positive base 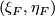 tangent to
tangent to  , where the orientation on
, where the orientation on  comes from
comes from  . The union
. The union 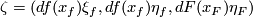 of the images of the constructed bases is a base at
of the images of the constructed bases is a base at 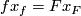 of
of  . If
. If  is positive, then call the tangent base
is positive, then call the tangent base 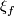 of
of  `positive'. Since a change of the orientation on
`positive'. Since a change of the orientation on  forces a change of the orientation of
forces a change of the orientation of  , this condition indeed defines an orientation on
, this condition indeed defines an orientation on  .
.
Definition 5.2.
Assume that 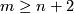 .
Take a general position homotopy
.
Take a general position homotopy 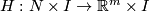 between
between  and
and  .
.
Tex syntax errorof the self-intersection set carries a cycle mod 2. If
 is oriented and
is oriented and  is odd, the closure also carries an integer cycle. See [Hudson1967,
is odd, the closure also carries an integer cycle. See [Hudson1967,  11], [Skopenkov2006,
11], [Skopenkov2006,  2.3 `The Whitney obstruction'].
2.3 `The Whitney obstruction'].
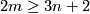 by general position the closure
by general position the closure Tex syntax errorcan be assumed to be a submanifold. In general, since
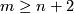 , by general position the closure has codimension 2 singularities, as defined in
, by general position the closure has codimension 2 singularities, as defined in  7. So the closure carries a cycle mod 2. When
7. So the closure carries a cycle mod 2. When  is odd the closure also has a canonical orientation (see Definition 7.1 and Remark 7.2), so the closure carries an integer cycle.
is odd the closure also has a canonical orientation (see Definition 7.1 and Remark 7.2), so the closure carries an integer cycle.
Define the Whitney invariant to be the homology class:
Tex syntax error
Clearly, 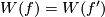 if
if  is isotopic to
is isotopic to  .
Hence the Whitney invariant defines a map
.
Hence the Whitney invariant defines a map
![\displaystyle W:E^m(N)\to H_{2n-m+1}(N;\Zz_N),\quad [f] \mapsto W(f).](/images/math/c/3/0/c30f51328f41351aac3861e4f870de3e.png)
Clearly, 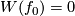 (for both definitions).
(for both definitions).
The definition of  depends on the choice of
depends on the choice of  , but we write
, but we write  not
not 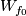 for brevity.
for brevity.
Remark 5.3.
(a) The Whitney invariant is well-defined by Definition 5.2,
i.e. is independent of the choice of a general position homotopy 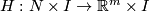 from
from  to
to  .
.
Tex syntax errorfor a general position homotopy
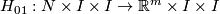 between general position homotopies
between general position homotopies 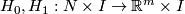 from
from  to
to  . See details in [Hudson1969,
. See details in [Hudson1969,  11].
11].
(b) Definition 5.1 is a particular case of Definition 5.2.
(Indeed, if 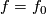 on
on  , we can take
, we can take  to be fixed on
to be fixed on  . See details in [Skopenkov2010, Difference
Lemma 2.4].)
Hence the Whitney invariant is well-defined by Definition 5.1, i.e. independent of the choice
of
. See details in [Skopenkov2010, Difference
Lemma 2.4].)
Hence the Whitney invariant is well-defined by Definition 5.1, i.e. independent of the choice
of  and of the isotopy making
and of the isotopy making 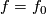 outside
outside  .
.
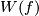 is independent of the choice of the orientation on
is independent of the choice of the orientation on  (because a change of the orientation on
(because a change of the orientation on  forces a change of the orientation on
forces a change of the orientation on  or on
or on Tex syntax error). For the reflection
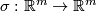 with respect to a hyperplane we have
with respect to a hyperplane we have 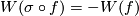 (because a change of the orientation on
(because a change of the orientation on  forces a change of the orientation on
forces a change of the orientation on  or on
or on Tex syntax error; for Definition 5.1 also observe that we may assume that
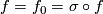 on
on  ).
).
(d) For the Hudson tori 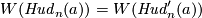 is
is  or
or  for
for  ,
and
,
and 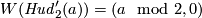 .
.
For  this is clear by Definition 5.1. For
this is clear by Definition 5.1. For 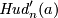 and
and  this was proved in [Hudson1963] (with a different but equivalent definition of the Whitney invariant; using and proving a particular case of Remark 5.3.f). For
this was proved in [Hudson1963] (with a different but equivalent definition of the Whitney invariant; using and proving a particular case of Remark 5.3.f). For 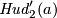 the proof is analogous.
the proof is analogous.
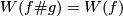 for any pair of embeddings
for any pair of embeddings  and
and 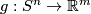 . This is clear by Definition 5.1 because
. This is clear by Definition 5.1 because 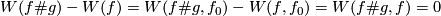 . Let us prove the latter equality. Take the identical isotopy
. Let us prove the latter equality. Take the identical isotopy 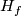 of
of  and a general position homotopy
and a general position homotopy 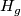 between
between  and the standard embedding. Then the boundary connected sum
and the standard embedding. Then the boundary connected sum 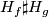 is a general position homotopy between
is a general position homotopy between 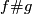 and an embedding isotopic to
and an embedding isotopic to  . The cycle
. The cycle Tex syntax erroris null-homologous in
 and hence in
and hence in 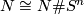 ; cf. [Skopenkov2008, Addendum to the Classification Theorem].
; cf. [Skopenkov2008, Addendum to the Classification Theorem].
(f) For 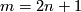 and
and 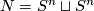 the Whitney invariant equals to the pair of linking coefficients [Skopenkov2016h,
the Whitney invariant equals to the pair of linking coefficients [Skopenkov2016h,  3].
3].
(g) The Whitney invariant need not be a bijection for 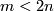 . This is seen, for example, by applying Theorem 6.4 below in case of knotted tori [Skopenkov2016k, Theorem 5.1]) or by taking
. This is seen, for example, by applying Theorem 6.4 below in case of knotted tori [Skopenkov2016k, Theorem 5.1]) or by taking  even,
even,  non-orientable,
non-orientable, 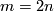 and applying by Theorem 2.1.b.
and applying by Theorem 2.1.b.
6 A generalization to highly-connected manifolds
In this section let  be a closed orientable homologically
be a closed orientable homologically  -connected
-connected  -manifold,
-manifold, 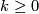 . Recall the unknotting theorem [Skopenkov2016c, Theorem 2.4] that all embeddings
. Recall the unknotting theorem [Skopenkov2016c, Theorem 2.4] that all embeddings 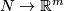 are isotopic when
are isotopic when 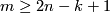 and
and 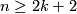 . In this section we generalize Theorem 2.1 to a description of
. In this section we generalize Theorem 2.1 to a description of 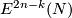 and further to
and further to 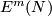 for
for 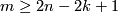 .
.
6.1 Examples
Some simple examples are the Hudson tori 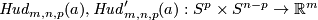 .
.
Example 6.1 (cf. [Skopenkov2010, Definition 1.4]).
Assume that  is
is  -connected and
-connected and 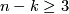 .
Then for an embedding
.
Then for an embedding 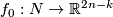 and a class
and a class 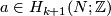 one can construct an embedding
one can construct an embedding 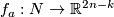 by linked embedded connected sum analogously to the case
by linked embedded connected sum analogously to the case 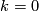 presented in Example 4.1.
presented in Example 4.1.
We have 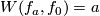 for the Whitney invariant. Hence by Theorem 6.2 below this construction gives a free transitive action of
for the Whitney invariant. Hence by Theorem 6.2 below this construction gives a free transitive action of 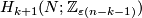 on
on 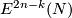 , provided
, provided 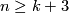 or
or 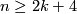 in the PL or smooth categories, respectively.
in the PL or smooth categories, respectively.
The embedding 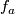 has an alternative construction using parametric connected sum [Skopenkov2014, Remark 18.a].
has an alternative construction using parametric connected sum [Skopenkov2014, Remark 18.a].
6.2 Classification
Theorem 6.2. Let  be a closed oriented homologically
be a closed oriented homologically  -connected
-connected  -manifold,
-manifold, 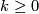 . Then the Whitney invariant
. Then the Whitney invariant
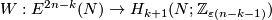
is a bijection, provided 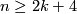 in the smooth category or
in the smooth category or 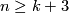 in the PL category.
in the PL category.
This was proved for  -connected manifolds in the smooth category [Haefliger&Hirsch1963, Theorem 2.4], and in the PL category in
[Weber1967], [Hudson1969,
-connected manifolds in the smooth category [Haefliger&Hirsch1963, Theorem 2.4], and in the PL category in
[Weber1967], [Hudson1969,  11], cf. [Boechat&Haefliger1970, Theorem 1.6], [Boechat1971, Theorem 4.2], [Vrabec1977, Theorems 1.1 and 1.2], [Adachi1993,
11], cf. [Boechat&Haefliger1970, Theorem 1.6], [Boechat1971, Theorem 4.2], [Vrabec1977, Theorems 1.1 and 1.2], [Adachi1993,  7]. The proof actually used the homological
7]. The proof actually used the homological  -connectedness assumption (basically because the
-connectedness assumption (basically because the  -connectedness was used to ensure high enough connectedness of the complement in
-connectedness was used to ensure high enough connectedness of the complement in  to the image of
to the image of  , by Alexander duality and simple connectedness of the complement, so homological
, by Alexander duality and simple connectedness of the complement, so homological  -connectedness of
-connectedness of  is sufficient).
is sufficient).
For 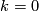 Theorem 6.2 is covered by Theorem 2.1; for
Theorem 6.2 is covered by Theorem 2.1; for 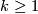 it is not.
For
it is not.
For 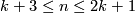 the PL case of Theorem 6.2 gives nothing but the Zeeman Unknotting Spheres Theorem [Skopenkov2016c, Theorem 2.3].
For the case of knotted tori see [Skopenkov2016k, Theorem 3.1].
the PL case of Theorem 6.2 gives nothing but the Zeeman Unknotting Spheres Theorem [Skopenkov2016c, Theorem 2.3].
For the case of knotted tori see [Skopenkov2016k, Theorem 3.1].
An inverse to the map  of Theorem 6.2 is given by Example 6.1.
of Theorem 6.2 is given by Example 6.1.
Because of the existence of knotted spheres the analogues of Theorem 6.2 for 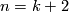 in the PL case, and for
in the PL case, and for 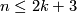 in the smooth case are false.
So for the smooth category,
in the smooth case are false.
So for the smooth category, 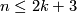 and
and  closed connected, a classification of
closed connected, a classification of 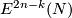 is much harder: for 40 years the only known complete readily calculable classification results were for homology spheres
is much harder: for 40 years the only known complete readily calculable classification results were for homology spheres  . E.g.
. E.g. 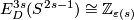 for any
for any 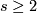 [Haefliger1966, Corollary 8.14], [Skopenkov2016s, Theorem 3.2].
The following result for
[Haefliger1966, Corollary 8.14], [Skopenkov2016s, Theorem 3.2].
The following result for 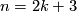 was obtained using the Boéchat-Haefliger formula for the smoothing obstruction [Boechat&Haefliger1970, Theorem 2.1], [Boechat1971, Theorem 5.1].
Using that formula one can define the higher-dimensional Kreck invariant [Skopenkov2008,
was obtained using the Boéchat-Haefliger formula for the smoothing obstruction [Boechat&Haefliger1970, Theorem 2.1], [Boechat1971, Theorem 5.1].
Using that formula one can define the higher-dimensional Kreck invariant [Skopenkov2008,  4].
4].
Theorem 6.3 [Skopenkov2008, Higher-dimensional Classification Theorem]. Let  be a closed orientable homologically
be a closed orientable homologically 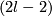 -connected
-connected 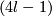 -manifold. Then the Whitney invariant
-manifold. Then the Whitney invariant
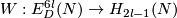
is surjective and for any 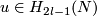 the Kreck invariant
the Kreck invariant
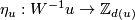
is a 1-1 correspondence, where 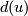 is the divisibility of the projection of
is the divisibility of the projection of  to the free part of
to the free part of 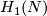 .
.
Recall that the divisibility of zero is zero and the divisibility of 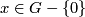 is
is 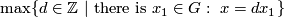 .
.
How does one describe 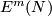 when
when  is not
is not 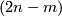 -connected?
For general
-connected?
For general  see the sentence on
see the sentence on 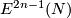 at the end of
at the end of  2.
We can say more as the connectivity
2.
We can say more as the connectivity  of
of  increases.
Some estimations of
increases.
Some estimations of 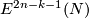 for a closed
for a closed  -connected
-connected  -manifold
-manifold  are presented in [Skopenkov2010]. For
are presented in [Skopenkov2010]. For 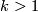 one can go even further:
one can go even further:
Theorem 6.4 [Becker&Glover1971, Corollary 1.3]. Let  be a closed
be a closed  -connected
-connected  -manifold embeddable into
-manifold embeddable into  ,
, 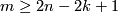 and
and 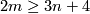 . Then there is a 1-1 correspondence
. Then there is a 1-1 correspondence
![\displaystyle E^m(N)\to [N_0, V_{m,n+1}].](/images/math/6/4/3/643341df90bc99621c0740a72f5ab4ef.png)
The 1-1 correspondence is constructed using `the Haefliger-Wu invariant' involving the configuration space of distinct pairs [Skopenkov2006,  5].
For
5].
For 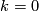 Theorem 6.4 is the same as General Position Theorem [Skopenkov2016c, Theorem 2.1] (because
Theorem 6.4 is the same as General Position Theorem [Skopenkov2016c, Theorem 2.1] (because 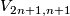 is
is  -connected).
For
-connected).
For 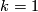 Theorem 6.4 is covered by Theorem 6.2; for
Theorem 6.4 is covered by Theorem 6.2; for 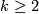 it is not.
For application to knotted tori see [Skopenkov2016k, Theorem 5.1].
For generalization to arbitrary manifolds see survey [Skopenkov2006,
it is not.
For application to knotted tori see [Skopenkov2016k, Theorem 5.1].
For generalization to arbitrary manifolds see survey [Skopenkov2006,  5] and [Haefliger1963], [Weber1967], [Skopenkov2002]. Observe that in Theorem 6.4
5] and [Haefliger1963], [Weber1967], [Skopenkov2002]. Observe that in Theorem 6.4 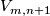 can be replaced by
can be replaced by 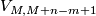 for any
for any 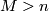 .
.
7 An orientation on the self-intersection set
 be a smooth map from an oriented
be a smooth map from an oriented  -manifold
-manifold  where
where 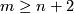 . We assume that the closure
. We assume that the closure Tex syntax errorof the self-intersection set of
 has codimension 2 singularities, i.e., there is
has codimension 2 singularities, i.e., there is Tex syntax errorsuch that
- both
 and
and Tex syntax error
are subpolyhedra of some triangulation of ,
,
- we have
 and
and
-
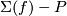 is an open manifold consisting of self-transverse double points of
is an open manifold consisting of self-transverse double points of  .
.
Definition 7.1 (A canonical orientation on 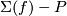 ).
Take points
).
Take points 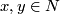 away from
away from  and such that
and such that 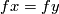 . Then a
. Then a 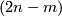 -base
-base 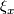 tangent to
tangent to 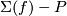 at
at  gives a
gives a  -base
-base 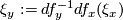 tangent to
tangent to 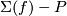 at
at  . Since
. Since  is oriented, we can take positive
is oriented, we can take positive 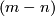 -bases
-bases 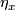 and
and 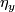 at
at  and
and  normal to
normal to 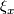 and to
and to 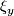 . If the base
. If the base 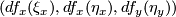 of
of  is positive, then call the base
is positive, then call the base 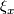 positive. This is well-defined because a change of the sign of
positive. This is well-defined because a change of the sign of 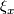 forces changes of the signs of
forces changes of the signs of 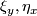 and
and 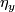 .
.
Remark 7.2 (Properties of the orientation just defined on 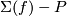 )..
)..
- A change of the orientation of
 forces changes of the signs of
forces changes of the signs of 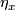 and
and 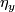 and so does not change the orientation of
and so does not change the orientation of 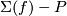 .
.
- The orientation on
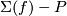 need not extend to
need not extend to Tex syntax error
: take the smooth cone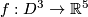 over a general position map
over a general position map 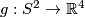 having only two transverse self-intersection points, where the smooth cone is defined by
having only two transverse self-intersection points, where the smooth cone is defined by 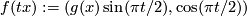 , for
, for 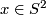 and
and ![t\in[0,1]](/images/math/4/0/d/40de672f62756d608425bb0e58f1dfa1.png) .
.
- The orientation on
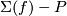 extends to
extends to Tex syntax error
if is odd [Hudson1969, Lemma 11.4].
is odd [Hudson1969, Lemma 11.4].
Remark 7.3 (A canonical orientation on 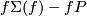 for
for  even).
This remark is added as a complement for Definition 7.1 but is not needed for the definition of the Whitney invariant.
even).
This remark is added as a complement for Definition 7.1 but is not needed for the definition of the Whitney invariant.
Take a 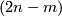 -base
-base  at a point
at a point 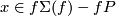 . Since
. Since  is oriented, we can take a positive
is oriented, we can take a positive 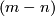 -base
-base 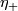 normal to
normal to 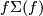 in one sheet of
in one sheet of 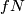 . Analogously construct an
. Analogously construct an 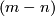 -base
-base 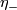 for the other sheet of
for the other sheet of 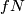 .
Since
.
Since  is even, the orientation of the base
is even, the orientation of the base 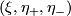 of
of  does not depend on choosing the first and the other sheet of
does not depend on choosing the first and the other sheet of 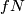 at
at  .
If the base
.
If the base 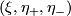 is positive, then call the base
is positive, then call the base  positive.
This is well-defined because a change of the sign of
positive.
This is well-defined because a change of the sign of  forces changes of the signs of
forces changes of the signs of 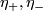 and so of
and so of 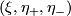 .
.
We remark that a change of the orientation of  forces changes of the signs of
forces changes of the signs of 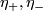 and so does not change the orientation of
and so does not change the orientation of 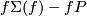 .
.
8 References
- [Adachi1993] M. Adachi, Embeddings and immersions, Translated from the Japanese by Kiki Hudson. Translations of Mathematical Monographs, 124. Providence, RI: American Mathematical Society (AMS), 1993. MR1225100 (95a:57039) Zbl 0810.57001
- [Avvakumov2017] S. Avvakumov, The classification of linked 3-manifolds in 6-space, Algebraic & Geometric Topology, to appear. arxiv preprint.
- [Bausum1975] D. R. Bausum, Embeddings and immersions of manifolds in Euclidean space, Trans. Amer. Math. Soc. 213 (1975), 263–303. MR0474330 (57 #13976) Zbl 0323.57017
- [Becker&Glover1971] J. Becker and H. Glover, Note on the embedding of manifolds in Euclidean space, Proc. Am. Math. Soc. 27 (1971), 405-410. MR0268903 (42 #3800) Zbl 0207.22402
- [Boechat&Haefliger1970] J. Boéchat and A. Haefliger, Plongements différentiables des variétés orientées de dimension
 dans
dans 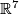 , (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
, (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
- [Boechat1971] J. Boéchat, Plongements de variétées différentiables orientées de dimension
 dans
dans 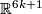 , Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
, Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
- [Haefliger&Hirsch1963] A. Haefliger and M. W. Hirsch, On the existence and classification of differentiable embeddings, Topology 2 (1963), 129–135. see also MR0149494 (26 #6981) Zbl 0113.38607
- [Haefliger1962b] A. Haefliger, Plongements de variétés dans le domain stable, Séminaire Bourbaki, 245 (1962).
- [Haefliger1963] A. Haefliger, Plongements différentiables dans le domain stable., Comment. Math. Helv.37 (1963), 155-176.
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Hudson1963] J. F. P. Hudson, Knotted tori, Topology 2 (1963), 11–22. MR0146829 (26 #4349) Zbl 0151.32503
- [Hudson1967] J. Hudson, Piecewise linear embeddings, Ann. of Math. (2) 85 (1967) 1–31. MR0215308 (35 #6149) Zbl 0153.25601
- [Hudson1969] J. F. P. Hudson, Piecewise linear topology, W. A. Benjamin, Inc., New York-Amsterdam, 1969. MR0248844 (40 #2094) Zbl 0189.54507
- [Koschorke2013] U. Koschorke, Immersion, http://www.map.mpim-bonn.mpg.de/Immersion
- [Milnor&Stasheff1974] J. W. Milnor and J. D. Stasheff, Characteristic classes, Princeton University Press, Princeton, N. J., 1974. MR0440554 (55 #13428) Zbl 1079.57504
- [Saeki1999] O. Saeki, On punctured 3-manifolds in 5-sphere, Hiroshima Math. J. 29 (1999) 255--272, MR1704247 (2000h:57045)
- [Skopenkov1997] A. Skopenkov, On the deleted product criterion for embeddability of manifolds in
 , Comment. Math. Helv. 72 (1997), 543-555.
, Comment. Math. Helv. 72 (1997), 543-555.
- [Skopenkov2002] A. Skopenkov, On the Haefliger-Hirsch-Wu invariants for embeddings and immersions., Comment. Math. Helv. 77 (2002), no.1, 78-124. MRMR1898394 (2003c:57023) Zbl 1012.57035
- [Skopenkov2005] A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, Topol. Appl., 157 (2010) 2094-2110. Available at the arXiv:0512594.
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2006a] A. Skopenkov, Classification of embeddings below the metastable dimension. Available at the arXiv:0607422.
- [Skopenkov2008] A. Skopenkov, A classification of smooth embeddings of 3-manifolds in 6-space, Math. Z. 260 (2008), no.3, 647–672. Available at the arXiv:0603429MR2434474 (2010e:57028) Zbl 1167.57013
- [Skopenkov2010] A. Skopenkov, Embeddings of k-connected n-manifolds into
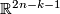 , Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
, Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
- [Skopenkov2014] A. Skopenkov, How do autodiffeomorphisms act on embeddings, Proc. A of the Royal Society of Edinburgh, 148:4 (2018) 835--848.
- [Skopenkov2015a] A. Skopenkov, A classification of knotted tori, Proc. A of the Royal Society of Edinburgh, 150:2 (2020), 549-567. Full version: http://arxiv.org/abs/1502.04470
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016f] A. Skopenkov, 4-manifolds in 7-space, to appear in Bull. Man. Atl.
- [Skopenkov2016h] A. Skopenkov, High codimension links, to appear in Bull. Man. Atl.
- [Skopenkov2016k] A. Skopenkov, Knotted tori, preprint.
- [Skopenkov2016s] A. Skopenkov, Knots, i.e. embeddings of spheres, preprint.
- [Skopenkov2016t] A. Skopenkov, 3-manifolds in 6-space, to appear in Boll. Man. Atl.
- [Takase2006] M. Takase, Homology 3-spheres in codimension three, Internat. J. Math. 17 (2006), no.8, 869–885.
arxiv:math/0506464 MR2261638 (2007g:57049) Zbl 1113.57013
- [Tonkonog2010] D. Tonkonog, Embedding punctured $n$-manifolds in Euclidean $(2n-1)$-space
- [Vrabec1977] J. Vrabec, Knotting a
 -connected closed
-connected closed 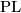
 -manifold in
-manifold in 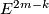 , Trans. Amer. Math. Soc. 233 (1977), 137–165. MR0645405 (58 #31097) Zbl 386.57013
, Trans. Amer. Math. Soc. 233 (1977), 137–165. MR0645405 (58 #31097) Zbl 386.57013
- [Weber1967] C. Weber, Plongements de polyedres dans le domaine metastable, Comment. Math. Helv. 42 (1967), 1-27. MR0238330 (38 #6606) Zbl 0152.22402
- [Yasui1984] T. Yasui, Enumerating embeddings of
 -manifolds in Euclidean
-manifolds in Euclidean 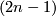 -space, J. Math. Soc. Japan 36 (1984), no.4, 555–576. MR759414 Zbl 0557.57019
-space, J. Math. Soc. Japan 36 (1984), no.4, 555–576. MR759414 Zbl 0557.57019