Template:Skopenkov2006
A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
[edit] 1 Comment
The last sentence of subsection `The Generalized Haefliger-Wu invariant' of  5 stated that for each subgroup
5 stated that for each subgroup  of
of 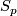 , the complex/manifold
, the complex/manifold  and the number
and the number  from the Non-embeddability Examples 5.9 there is a
from the Non-embeddability Examples 5.9 there is a  -equivariant map
-equivariant map 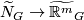 . Only a weaker statement for
. Only a weaker statement for 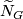 replaced by its simplicial version is obvious. For Example 5.9.c the weaker statement follows from the existence of an almost embedding
replaced by its simplicial version is obvious. For Example 5.9.c the weaker statement follows from the existence of an almost embedding 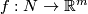 [Segal&Skopenkov&Spiez1998, Example in p. 338]. Those
[Segal&Skopenkov&Spiez1998, Example in p. 338]. Those  -equivariant maps are defined as
-equivariant maps are defined as 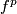 . Thus those maps are coherent for different
. Thus those maps are coherent for different  in the sense described in [Arone&Krushkal2021].
in the sense described in [Arone&Krushkal2021].
The stated assertion is presumably correct, but the proof could require particular properties of the almost embeddings constructed in the example.
In the last paragraph of this subsection it is stated that 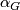 is not injective for each
is not injective for each  (and some
(and some 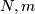 ). Analogously, only a weaker statement for
). Analogously, only a weaker statement for 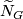 replaced by its simplicial version is obvious.
replaced by its simplicial version is obvious.
[edit] 2 References
- [Arone&Krushkal2021] G. Arone, V. Krushkal, Embedding obstructions in
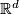 from the Goodwillie-Weiss calculus and Whitney disks, arxiv preprint.
from the Goodwillie-Weiss calculus and Whitney disks, arxiv preprint.
- [Segal&Skopenkov&Spiez1998] J. Segal, A. Skopenkov and S. Spie\. z, Embeddings of polyhedra in
 and the deleted product obstruction, Topol. Appl. 85 (1998), 225-234.
and the deleted product obstruction, Topol. Appl. 85 (1998), 225-234.