Parametric connected sum
(→Parametric connected sum along thickenings) |
|||
| (27 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
| + | {{Stub}} | ||
== Introduction == | == Introduction == | ||
<wikitex>; | <wikitex>; | ||
| − | Parametric connected sum is an operation on compact connected n-manifolds $M$ and $N$ equipped with codimension 0-embeddings $\phi: T \to M$ and $\psi : T \to N$ of a compact connected manifold $T$. It generalises the usual connected sum operation | + | Parametric connected sum is an operation on compact connected n-manifolds $M$ and $N$ equipped with codimension 0-embeddings $\phi: T \to M$ and $\psi : T \to N$ of a compact connected manifold $T$. It generalises the usual [[Connected sum|connected sum]] operation |
| − | + | which is the special case when $T = D^n$ is the $n$-disc. | |
| − | + | The parametric connected sum operation is more complicated than the usual connected | |
| − | + | sum operation since the isotopy classes of the embeddings of $T$ into $M$ may be significantly more complicated than the isotopy classes of embeddings of n-discs need for connected sum: these last are determined by (local) orientations. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
</wikitex> | </wikitex> | ||
== Connected sum along k-spheres == | == Connected sum along k-spheres == | ||
<wikitex>; | <wikitex>; | ||
| − | We say above that to define connected sum for connected k-manifolds $M$ and $N$ it is sufficient to equip them with an isotopy class of embeddings of the k-disc. | + | We say above that to define connected sum for connected k-manifolds $M$ and $N$ it is sufficient to equip them with an isotopy class of embeddings of the k-disc. Moreover, the disjoint union $D^n \sqcup D^n$ is the unique [[thickening]] of $S^0$. This motivates the following |
{{beginthm|Defintion}} | {{beginthm|Defintion}} | ||
| − | + | A manifold with an $S^k$-[[thickening]], an $S^k$-thickened manifold for short, is a pair $(M, \phi)$ where $M$ is a compact connected manifold and $\phi : S^k \times D^{n-k} \to \mathrm{int}(M)$ is an embedding. | |
{{endthm}} | {{endthm}} | ||
{{beginthm|Defintion}} | {{beginthm|Defintion}} | ||
| − | Let $M = (M, \phi)$ and $N = (N, \psi)$ by $S^k$- | + | Let $M = (M, \phi)$ and $N = (N, \psi)$ by $S^k$-thickened manifolds. Define |
| − | $$ M \sharp_k N = (M - \phi(S^k \times \{ 0 \}) \cup (N - \psi(S^k \times \{ 0 \})/simeq$$ | + | $$ M \sharp_k N = (M - \phi(S^k \times \{ 0 \}) \cup (N - \psi(S^k \times \{ 0 \})/\simeq$$ |
where $\simeq$ is defined via the embeddings $\phi$ and $\psi$. | where $\simeq$ is defined via the embeddings $\phi$ and $\psi$. | ||
{{endthm}} | {{endthm}} | ||
| − | + | It is clear that we have the following | |
{{beginthm|Observation}} | {{beginthm|Observation}} | ||
The diffeomorphism type of $M \sharp_k N$ depends only upon the the isotopy classes of the embeddings $\phi$ and $\psi$ (which of course includes the diffeomorphism types of $M$ and $N$). | The diffeomorphism type of $M \sharp_k N$ depends only upon the the isotopy classes of the embeddings $\phi$ and $\psi$ (which of course includes the diffeomorphism types of $M$ and $N$). | ||
| Line 43: | Line 30: | ||
=== Applications === | === Applications === | ||
<wikitex>; | <wikitex>; | ||
| − | The operation of $S^k$-connected sum was used in \cite{Ajala1984} and \cite{Ajala1987} to describe the set of smooth structures on the product of spheres $\Pi_{i=1}^r S^{n_i}$. | + | The operation of $S^k$-connected sum was used in \cite{Ajala1984} and \cite{Ajala1987} to describe the set of smooth structures on the product of spheres $\Pi_{i=1}^r S^{n_i}$. This construction also appears in \cite{Sako1981}. |
| + | |||
| + | The analogue of such a construction for [[Embeddings_in_Euclidean_space:_an_introduction_to_their_classification|embeddings]], the $S^k$-parametric connected sum of embeddings, is used | ||
| + | * to define, for $m\ge 2p+q+3$, a group stucture on the set $E^m(S^p \times S^q)$ of (smooth or PL) isotopy classes of embeddings $S^p \times S^q\to \Rr^m$ \cite{Skopenkov2006}, \S3.4, \cite{Skopenkov2006a}, \S3, \cite{Skopenkov2015a}. | ||
| + | * to construct an action of this group on the set of isotopy classes of embeddings of certain $(p+q)$-manifolds into $\Rr^m$ \cite{Skopenkov2014}, 1.2. | ||
| + | * to estimate the set of isotopy classes of embeddings \cite{Cencelj&Repovš&Skopenkov2007}, \cite{Cencelj&Repovš&Skopenkov2008}, \cite{Skopenkov2007}, \cite{Skopenkov2010}, \cite{Skopenkov2015}, \cite{Skopenkov2015a}, \cite{Crowley&Skopenkov2016} and unpublished paper \cite{Crowley&Skopenkov2016a}. | ||
</wikitex> | </wikitex> | ||
| Line 49: | Line 41: | ||
<wikitex>; | <wikitex>; | ||
Let $B$ be a [[stable fibred vector bundle]]. A foundational theorem of modified surgery is | Let $B$ be a [[stable fibred vector bundle]]. A foundational theorem of modified surgery is | ||
| − | {{beginthm|Theorem|Stable classification: \cite{Kreck1985}, \cite{Kreck1999}}} | + | {{beginthm|Theorem|Stable classification: \cite{Kreck1985|Theorem 2.1, p 19}, \cite{Kreck1999}, \cite{Kreck2016|Theorem 6.2}}} |
$$ NSt_{2n}(B) \cong \Omega_{2n}^B.$$ | $$ NSt_{2n}(B) \cong \Omega_{2n}^B.$$ | ||
{{endthm}} | {{endthm}} | ||
| − | In particular, $NSt_{2n}(B)$ has the structure of an abelian group. The question of whether there is a geometric definition of this group structure is taken up in \cite{Kreck1985|Chapter 2, pp | + | In particular, $NSt_{2n}(B)$ has the structure of an abelian group. The question of whether there is a geometric definition of this group structure is taken up in \cite{Kreck1985|Chapter 2, pp 25-6} where it is shown how to use parametric connected sum along thickenings to define an addition of stable diffeomorphism classes of closed $2n$-$B$-manifolds. This is described in more detail (for $n>2$) in \cite{Kreck2016|Section 6} and uses Wall's theory of thickenings, developed in \cite{Wall1966a}. More precisely, it depends on Wall's embedding theorem \cite{Wall1966a|p 76} for the existence of (unique up to concordance) embedded thickenings of the $(n-1)$-skeleton of $B$, and Wall's classification of thickenings in the stable range \cite{Wall1966a|Proposition 5.1} to ensure that two such embedded thickenings are diffeomorphic as $B$-manifolds, so that one may cut out their interiors and glue the resulting $B$-manifolds along the boundaries of the embedded thickenings. The special case of $n=2$ is discussed separately in \cite{Kreck2016|Section 5} under the name "connected sum along the $1$-skeleton". |
| + | </wikitex> | ||
<!--{{beginthm|Remark}} | <!--{{beginthm|Remark}} | ||
For an detailed exposition and extensive application of the modified surgery techniques of stable classifcaiton of 4-manifolds, see \cite{Teichner}. | For an detailed exposition and extensive application of the modified surgery techniques of stable classifcaiton of 4-manifolds, see \cite{Teichner}. | ||
| − | {{endthm}} -- | + | {{endthm}}--> |
| − | + | ||
== References == | == References == | ||
{{#RefList:}} | {{#RefList:}} | ||
| − | + | <!-- --> | |
| − | [[Category: | + | [[Category:Definitions]] |
| − | + | ||
Latest revision as of 02:04, 8 April 2020
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
[edit] 1 Introduction
Parametric connected sum is an operation on compact connected n-manifolds  and
and  equipped with codimension 0-embeddings
equipped with codimension 0-embeddings 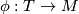 and
and 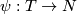 of a compact connected manifold
of a compact connected manifold  . It generalises the usual connected sum operation
which is the special case when
. It generalises the usual connected sum operation
which is the special case when 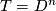 is the
is the  -disc.
The parametric connected sum operation is more complicated than the usual connected
sum operation since the isotopy classes of the embeddings of
-disc.
The parametric connected sum operation is more complicated than the usual connected
sum operation since the isotopy classes of the embeddings of  into
into  may be significantly more complicated than the isotopy classes of embeddings of n-discs need for connected sum: these last are determined by (local) orientations.
may be significantly more complicated than the isotopy classes of embeddings of n-discs need for connected sum: these last are determined by (local) orientations.
[edit] 2 Connected sum along k-spheres
We say above that to define connected sum for connected k-manifolds  and
and  it is sufficient to equip them with an isotopy class of embeddings of the k-disc. Moreover, the disjoint union
it is sufficient to equip them with an isotopy class of embeddings of the k-disc. Moreover, the disjoint union  is the unique thickening of
is the unique thickening of 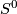 . This motivates the following
. This motivates the following
Defintion 2.1.
A manifold with an 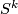 -thickening, an
-thickening, an 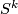 -thickened manifold for short, is a pair
-thickened manifold for short, is a pair 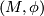 where
where  is a compact connected manifold and
is a compact connected manifold and 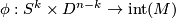 is an embedding.
is an embedding.
Defintion 2.2.
Let 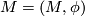 and
and 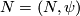 by
by 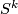 -thickened manifolds. Define
-thickened manifolds. Define
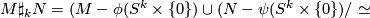
where 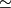 is defined via the embeddings
is defined via the embeddings  and
and 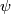 .
.
It is clear that we have the following
Observation 2.3.
The diffeomorphism type of 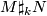 depends only upon the the isotopy classes of the embeddings
depends only upon the the isotopy classes of the embeddings  and
and 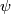 (which of course includes the diffeomorphism types of
(which of course includes the diffeomorphism types of  and
and  ).
).
[edit] 2.1 Applications
The operation of 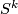 -connected sum was used in [Ajala1984] and [Ajala1987] to describe the set of smooth structures on the product of spheres
-connected sum was used in [Ajala1984] and [Ajala1987] to describe the set of smooth structures on the product of spheres 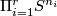 . This construction also appears in [Sako1981].
. This construction also appears in [Sako1981].
The analogue of such a construction for embeddings, the 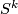 -parametric connected sum of embeddings, is used
-parametric connected sum of embeddings, is used
- to define, for
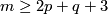 , a group stucture on the set
, a group stucture on the set 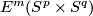 of (smooth or PL) isotopy classes of embeddings
of (smooth or PL) isotopy classes of embeddings 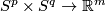 [Skopenkov2006], \S3.4, [Skopenkov2006a], \S3, [Skopenkov2015a].
[Skopenkov2006], \S3.4, [Skopenkov2006a], \S3, [Skopenkov2015a].
- to construct an action of this group on the set of isotopy classes of embeddings of certain
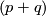 -manifolds into
-manifolds into  [Skopenkov2014], 1.2.
[Skopenkov2014], 1.2.
- to estimate the set of isotopy classes of embeddings [Cencelj&Repovš&Skopenkov2007], [Cencelj&Repovš&Skopenkov2008], [Skopenkov2007], [Skopenkov2010], [Skopenkov2015], [Skopenkov2015a], [Crowley&Skopenkov2016] and unpublished paper [Crowley&Skopenkov2016a].
[edit] 3 Parametric connected sum along thickenings
Let  be a stable fibred vector bundle. A foundational theorem of modified surgery is
be a stable fibred vector bundle. A foundational theorem of modified surgery is
Theorem 3.1 Stable classification: [Kreck1985, Theorem 2.1, p 19], [Kreck1999], [Kreck2016, Theorem 6.2].
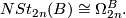
In particular, 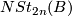 has the structure of an abelian group. The question of whether there is a geometric definition of this group structure is taken up in [Kreck1985, Chapter 2, pp 25-6] where it is shown how to use parametric connected sum along thickenings to define an addition of stable diffeomorphism classes of closed
has the structure of an abelian group. The question of whether there is a geometric definition of this group structure is taken up in [Kreck1985, Chapter 2, pp 25-6] where it is shown how to use parametric connected sum along thickenings to define an addition of stable diffeomorphism classes of closed  -
- -manifolds. This is described in more detail (for
-manifolds. This is described in more detail (for 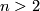 ) in [Kreck2016, Section 6] and uses Wall's theory of thickenings, developed in [Wall1966a]. More precisely, it depends on Wall's embedding theorem [Wall1966a, p 76] for the existence of (unique up to concordance) embedded thickenings of the
) in [Kreck2016, Section 6] and uses Wall's theory of thickenings, developed in [Wall1966a]. More precisely, it depends on Wall's embedding theorem [Wall1966a, p 76] for the existence of (unique up to concordance) embedded thickenings of the  -skeleton of
-skeleton of  , and Wall's classification of thickenings in the stable range [Wall1966a, Proposition 5.1] to ensure that two such embedded thickenings are diffeomorphic as
, and Wall's classification of thickenings in the stable range [Wall1966a, Proposition 5.1] to ensure that two such embedded thickenings are diffeomorphic as  -manifolds, so that one may cut out their interiors and glue the resulting
-manifolds, so that one may cut out their interiors and glue the resulting  -manifolds along the boundaries of the embedded thickenings. The special case of
-manifolds along the boundaries of the embedded thickenings. The special case of  is discussed separately in [Kreck2016, Section 5] under the name "connected sum along the
is discussed separately in [Kreck2016, Section 5] under the name "connected sum along the  -skeleton".
-skeleton".
[edit] 4 References
- [Ajala1984] S. O. Ajala, Differentiable structures on products of spheres, Houston J. Math. 10 (1984), no.1, 1–14. MR736571 (85c:57032) Zbl 0547.57026
- [Ajala1987] S. O. Ajala, Differentiable structures on a generalized product of spheres, Internat. J. Math. Math. Sci. 10 (1987), no.2, 217–226. MR886378 (88j:57028) Zbl 0627.57022
- [Cencelj&Repovš&Skopenkov2007] M. Cencelj, D. Repovš and M. Skopenkov, Homotopy type of the complement of an immersion and classification of embeddings of tori., Russ. Math. Surv.62 (2007), no.5, 985-987. Zbl 1141.57009
- [Cencelj&Repovš&Skopenkov2008] M. Cencelj, D. Repovš and M. Skopenkov, Classification of knotted tori in the 2-metastable dimension, Mat. Sbornik, 203:11 (2012), 1654-1681. Available at the arXiv:0811.2745.
- [Crowley&Skopenkov2016] D. Crowley and A. Skopenkov, Embeddings of non-simply-connected 4-manifolds in 7-space, I. Classification modulo knots, Moscow Math. J., 21 (2021), 43--98. arXiv:1611.04738.
- [Crowley&Skopenkov2016a] D. Crowley and A. Skopenkov, Embeddings of non-simply-connected 4-manifolds in 7-space, II. Smooth classification. Proc. A of the Royal Soc. of Edinburgh, to appear. arXiv:1612.04776
- [Kreck1985] M. Kreck, An extension of the results of Browder, Novikov and Wall about surgery on compact manifolds, preprint Mainz (1985).
- [Kreck1999] M. Kreck, Surgery and duality, Ann. of Math. (2) 149 (1999), no.3, 707–754. MR1709301 (2001a:57051) Zbl 0935.57039
- [Kreck2016] M. Kreck, Thoughts about a good classification of manifolds, Proceedings of the 22nd Gökova Geometry-Topology Conference (2016), 187–201. MR3526843 ()
- [Sako1981] Y. Sako, Connected sum along the cycle operation of
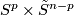 on
on  -manifolds, Proc. Japan Acad. Ser. A Math. Sci. 57 (1981), no.10, 499–502. MR640259 (83a:57043) Zbl 0505.57010
-manifolds, Proc. Japan Acad. Ser. A Math. Sci. 57 (1981), no.10, 499–502. MR640259 (83a:57043) Zbl 0505.57010
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2006a] A. Skopenkov, Classification of embeddings below the metastable dimension. Available at the arXiv:0607422.
- [Skopenkov2007] A. Skopenkov, A new invariant and parametric connected sum of embeddings, Fund. Math. 197 (2007), 253–269. arXiv:math/0509621. MR2365891 (2008k:57044) Zbl 1145.57019
- [Skopenkov2010] A. Skopenkov, Embeddings of k-connected n-manifolds into
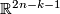 , Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
, Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
- [Skopenkov2014] A. Skopenkov, How do autodiffeomorphisms act on embeddings, Proc. A of the Royal Society of Edinburgh, 148:4 (2018) 835--848.
- [Skopenkov2015] M. Skopenkov, When is the set of embeddings finite up to isotopy? Intern. J. Math. 26:7 (2015), http://arxiv.org/abs/1106.1878
- [Skopenkov2015a] A. Skopenkov, A classification of knotted tori, Proc. A of the Royal Society of Edinburgh, 150:2 (2020), 549-567. Full version: http://arxiv.org/abs/1502.04470
- [Wall1966a] C. T. C. Wall, Classification problems in differential topology. IV. Thickenings, Topology 5 (1966), 73–94. MR0192509 (33 #734) Zbl 0149.20501