Template:Kreck1999
M. Kreck, Surgery and duality, Ann. of Math. (2) 149 (1999), no.3, 707–754. MR1709301 (2001a:57051) Zbl 0935.57039
[edit] 1 Comments
We consider the question of the surgery obstruction 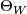 for a bordism
for a bordism
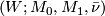 as in Theorem 3 but when the maps
as in Theorem 3 but when the maps 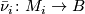 are normal
are normal 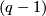 -smoothings. In this case, the proof of Theorem 3 shows that
if
-smoothings. In this case, the proof of Theorem 3 shows that
if 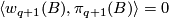 , then
, then
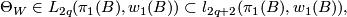
and if 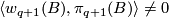 , then
, then
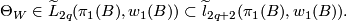
Here 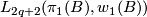 and
and 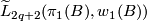 may be defined
as the groups of units in
may be defined
as the groups of units in 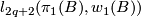 and
and 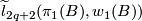 respectively. Alternatively, they may be defined as certain Witt groups of
quadratic forms over the twisted group ring
respectively. Alternatively, they may be defined as certain Witt groups of
quadratic forms over the twisted group ring ![(\Zz[\pi_1(B)], w_1(B))](/images/math/4/e/a/4eac9bfd408af1a9711b8342071490d7.png) . In the case
of the tilde groups, when
. In the case
of the tilde groups, when 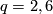 , one simply considers quadratic forms with values in
, one simply considers quadratic forms with values in
![\displaystyle Q_{-1}(\Zz[\pi_1(B)], w_1(B))/Q_{-1}(e).](/images/math/4/2/6/426e6c737bc347bbf1eff8ca99cf898d.png)
In particular, there are isomorphisms
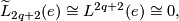
where 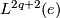 is the symmetric
is the symmetric  -group.
-group.
[edit] 2 Corrections
While their statements are correct, the proofs of both Proposition 4 and Theorem 1 of Section 3 are incorrect:
The supplied proof of Proposition 4 uses (on p. 718, right before Lemma 3) the fact that a finite cell complex has its higher homotopy groups finitely generated over its fundamental group-ring. This, however, is not the case in general, probably the easiest counterexample being 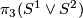 , due to the occurrence of Whitehead-products. It is in fact true that the lowest homotopy group of a map between finite cell complexes is finitely generated over the fundamental group ring of the source, once it induces an isomorphism on the fundamental group. This suffices to successively make a given normal map highly connected in the setup of proposition 4. Details can easily be adapted from Lück's Trieste notes.
, due to the occurrence of Whitehead-products. It is in fact true that the lowest homotopy group of a map between finite cell complexes is finitely generated over the fundamental group ring of the source, once it induces an isomorphism on the fundamental group. This suffices to successively make a given normal map highly connected in the setup of proposition 4. Details can easily be adapted from Lück's Trieste notes.
The mistake in the proof of Theorem 1 is a simply misquote of Proposition 4: It is claimed that a normal map from a given bordism  into the normal
into the normal  -type
-type  of a given manifold
of a given manifold  can be made into a
can be made into a  -equivalence by proposition 4, but this is not generally true: One way to formulate the assumption of Proposition 4 for achieving this is that
-equivalence by proposition 4, but this is not generally true: One way to formulate the assumption of Proposition 4 for achieving this is that  be of type
be of type 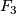 (generally, one calls a space
(generally, one calls a space  'of type
'of type 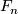 ' if it admits an
' if it admits an  -equivalence from a finite cell complex). However, while
-equivalence from a finite cell complex). However, while  is of course of type
is of course of type 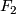 , it is not obviously of type
, it is not obviously of type 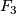 and indeed it need not be: From
and indeed it need not be: From  one still has a canonical
one still has a canonical  -equivalence to
-equivalence to 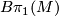 which is a
which is a  -equivalence if the universal cover of
-equivalence if the universal cover of  admits a spin-structure. If
admits a spin-structure. If  is of type
is of type 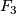 this exhibits
this exhibits 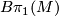 as being of type
as being of type 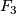 as well. However, it is well-known that an arbitrary finitely presented group can arise as the fundamental group of a closed, (spin!?)-manifold. Finitely presented groups are precisely those, whose classifying spaces are of type
as well. However, it is well-known that an arbitrary finitely presented group can arise as the fundamental group of a closed, (spin!?)-manifold. Finitely presented groups are precisely those, whose classifying spaces are of type 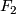 and it is generally true, that there are groups whose classifying spaces are of type
and it is generally true, that there are groups whose classifying spaces are of type 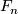 but not
but not 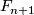 . To correct the argument one can use proposition 4 to produce a
. To correct the argument one can use proposition 4 to produce a  -equivalence from out of the map from
-equivalence from out of the map from  to
to  by surgeries in the interior of
by surgeries in the interior of  and then to surgeries by hand to make the inclusion
and then to surgeries by hand to make the inclusion 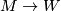 surjective on
surjective on 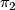 . That this is indeed possible is proven in Theorem 2.2 of Rosenberg's paper '
. That this is indeed possible is proven in Theorem 2.2 of Rosenberg's paper '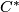 -algebras, positive scalar curvature, and the Novikov conjecture II' [Rosenberg1986] for the case of spin-manifolds and the proof immediately generalises.
-algebras, positive scalar curvature, and the Novikov conjecture II' [Rosenberg1986] for the case of spin-manifolds and the proof immediately generalises.