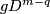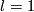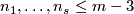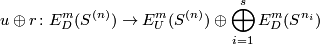High codimension links
Askopenkov (Talk | contribs) (→General position and the Hopf linking) |
Askopenkov (Talk | contribs) (→Classification in codimension at least 3) |
||
| (506 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{ | + | {{Authors|Askopenkov}} |
== Introduction == | == Introduction == | ||
<wikitex>; | <wikitex>; | ||
| − | + | Most of this page is intended not only for specialists in embeddings, but also for mathematician from other areas who want to apply or to learn the theory of embeddings. | |
| − | + | On this page we describe readily calculable classifications of embeddings of closed ''disconnected'' manifolds into $\Rr^m$ up to isotopy, and more generally of spaces which are a disjoint union of manifolds of varying dimensions. The presently known cases of such classifications are <!--embeddings | |
| − | + | $S^{n_1}\sqcup\ldots\sqcup S^{n_s}\to S^m$ for $m-3\ge n_i$ (under some further restrictions),--> embeddings $N_1\sqcup\ldots\sqcup N_s\to S^m$, where $N_1,\ldots, N_s$ are spheres (or even closed manifolds) and $m-3\ge\dim N_i$ for every $i$, under some further restrictions. For a related classification of knotted tori see \cite{Skopenkov2016k}. | |
| + | |||
| + | For an $s$-tuple $(n):=(n_1,\ldots,n_s)$ denote $S^{(n)}:=S^{n_1}\sqcup\ldots\sqcup S^{n_s}$. Although $S^{(n)}$ is not a manifold when $n_1,\ldots,n_s$ are not all equal, embeddings $S^{(n)}\to S^m$ and isotopy between such embeddings are defined analogously to [[Isotopy|the case of manifolds]] \cite{Skopenkov2016i}. Denote by $E^m(S^{(n)})$ the set of embeddings $S^{(n)}\to S^m$ up to isotopy. | ||
| + | |||
| + | For a [[Embeddings_in_Euclidean_space:_an_introduction_to_their_classification#Introduction|general introduction to embeddings]] as well as the [[Embeddings_in_Euclidean_space:_an_introduction_to_their_classification#Notation and conventions|notation and conventions]] used on this page, we refer to \cite[$\S$1, $\S$3]{Skopenkov2016c}. | ||
| + | |||
| + | The following table was obtained by Zeeman around 1960 (see the Haefliger-Zeeman Theorem \ref{lkhaze} below): | ||
| + | $$\begin{array}{c|c|c|c|c|c|c|c} | ||
| + | m &\ge2q+2 &2q+1 &2q\ge8 &2q-1\ge11 &2q-2\ge14 &2q-3\ge17 &2q-4\ge20 \\ | ||
| + | \hline | ||
| + | |E^m(S^q\sqcup S^q)| &1 &\infty &2 &2 &24 &1 &1 | ||
| + | \end{array}$$ | ||
| + | [[Image:EmbeddedConnectedSum.jpg|thumb|350px|Figure 1: Component-wise embedded connected sum]] | ||
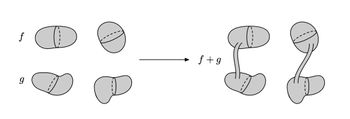
| + | A component-wise version of [[Embeddings_in_Euclidean_space:_an_introduction_to_their_classification#Embedded_connected_sum|embedded connected sum]] \cite[$\S$5]{Skopenkov2016c} defines a commutative group structure on the set $E^m(S^{(n)})$ for $m-3\ge n_i$ \cite[2.5]{Haefliger1966a}, \cite[Group Structure Lemma 2.2 and Remark 2.3.a]{Skopenkov2015}, \cite[$\S$1]{Avvakumov2016}, \cite[$\S$1.4]{Avvakumov2017}, see Figure 1. | ||
| + | |||
| + | The ''standard embedding'' $S^k\to D^m$ is defined by $(x_1, \ldots, x_{k+1})\mapsto(x_1, \ldots, x_{k+1}, 0, \ldots, 0)$. Fix $s$ pairwise disjoint $m$-discs $D^m_1\sqcup\ldots\sqcup D^m_s\subset S^m$. The ''standard embedding'' $S^{(n)}\to S^m$ is defined by taking the union of the compositions of the standard embeddings $S^{n_k} \to D^m_k$ with the fixed inclusions $D^m_k \to S^m$. <!-- {\rm i}_k $g\circ({\rm i}_{n_1}\sqcup\ldots\sqcup{\rm i}_s)$. in $S^m$, i.e. take an embedding $g:D^m_1\sqcup\ldots\sqcup D^m_s\to S^m$ We define the standard embedding $S^{(n)}\to S^m$ as follows. --> | ||
</wikitex> | </wikitex> | ||
| − | == | + | == Examples == |
<wikitex>; | <wikitex>; | ||
| − | + | [[Embeddings_in_Euclidean_space:_an_introduction_to_their_classification#Unknotting_theorems|Recall that]] for any $q$-manifold $N$ and $m\ge2q+2$, every two embeddings $N\to\Rr^m$ are isotopic \cite[General Position Theorem 2.1]{Skopenkov2016c}, \cite[General Position Theorem 2.1]{Skopenkov2006}. | |
| − | + | The following example shows that the restriction $m\ge2q+2$ is sharp for non-connected manifolds. | |
| − | {{ | + | |
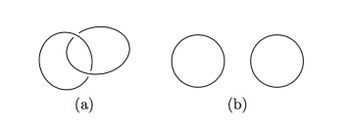
| + | {{beginthm|Example|(The Hopf Link)}}\label{hopf} | ||
| + | (a) For every positive integer $q$ there is an embedding $S^q\sqcup S^q\to\Rr^{2q+1}$, which is not isotopic to the standard embedding. | ||
| + | |||
| + | [[Image:HopfLink-and-TrivialLink.jpg|thumb|350px|Figure 2: The Hopf link (a) and the trivial link (b)]] | ||
| + | For $q=1$ the Hopf link is shown in Figure 2. For all $q$ the image of the Hopf link is the union of two $q$-spheres which can be described as follows: | ||
| + | |||
| + | * either the spheres are $\partial D^{q+1}\times0$ and $0\times\partial D^{q+1}$ in $\partial(D^{q+1}\times D^{q+1})\cong S^{2q+1}$; | ||
| + | |||
| + | * or they are given as the sets of points in $\Rr^{2q+1}$ satisfying the following equations: | ||
| + | $$\left\{\begin{array}{c} x_1=\dots=x_q=0\\ x_{q+1}^2+\dots+x_{2q+1}^2=1,\end{array}\right. \qquad\text{and}\qquad | ||
| + | \left\{\begin{array}{c} x_{q+2}=\dots=x_{2q+1}=0\\ x_1^2+\dots+x_q^2+(x_{q+1}-1)^2=1.\end{array}\right.$$ | ||
| + | This embedding is distinguished from the standard embedding by [[#The linking coefficient|the linking number]] (cf. $\S$\ref{s:inv}). | ||
| + | |||
| + | (b) For any $p,q$ there is an embedding $S^p\sqcup S^q\to\Rr^{p+q+1}$ which is not isotopic to the standard embedding. | ||
| + | |||
| + | Analogously to (a), the image is the union of two spheres which can be described as follows: | ||
| − | + | * either the spheres are $\partial D^{p+1}\times0$ and $0\times\partial D^{q+1}$ in $\partial(D^{p+1}\times D^{q+1})\cong S^{p+q+1}$. | |
| − | + | * or they are given as the points in $\Rr^{p+q+1}$ satisfying the following equations: | |
| − | + | $$\left\{\begin{array}{c} x_1=\dots=x_p=0\\ x_{p+1}^2+\dots+x_{p+q+1}^2=1,\end{array}\right. \qquad\text{and}\qquad | |
| + | \left\{\begin{array}{c} x_{p+2}=\dots=x_{p+q+1}=0\\ x_1^2+\dots+x_p^2+(x_{p+1}-1)^2=1.\end{array}\right.$$ | ||
| + | This embedding is also distinguished from the standard embedding by [[#The linking coefficient|the linking number]] (cf. $\S$\ref{s:inv}). | ||
{{endthm}} | {{endthm}} | ||
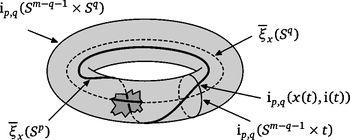
| − | + | {{beginthm|Definition|(A link with prescribed [[#The linking coefficient|linking coefficient]])}}\label{dz} | |
| − | + | We define the `Zeeman' map | |
| − | $$\ | + | [[Image:linking_coefficient.jpg|thumb|350px|Figure 3: A link with prescribed linking coefficient]] |
| − | + | $$\zeta=\zeta_{m,p,q}:\pi_p(S^{m-q-1})\to E^m(S^p\sqcup S^q)\quad\text{for}\quad p\le q.$$ | |
| − | $$\ | + | For a map $x:S^p\to S^{m-q-1}$ representing an element of $\pi_p(S^{m-q-1})$ let |
| − | + | $$\overline\zeta\phantom{}_x:S^p\to S^m\quad\text{be the composition}\quad | |
| − | + | S^p\overset{x\times{\rm i}}\to S^{m-q-1}\times S^q\overset{{\rm i}_{m,q}}\to S^m,$$ | |
| − | [ | + | see Figure 3. We have $\overline\zeta_x(S^p)\cap{\rm i}(S^q)\subset{\rm i}_{m,q}(S^{m-q-1}\times S^p)\cap{\rm i}_{m,q}(0\times S^q) =\emptyset$. Let $\zeta[x]:=[\overline\zeta_x\sqcup{\rm i}]$. |
| + | <!--where $i$ is the natural `standard embedding' defined in \cite[$\S$2.1]{Skopenkov2015a}--> | ||
| + | {{endthm}} | ||
| + | |||
| + | One can easily check that $\zeta$ is well-defined and is a homomorphism. | ||
</wikitex> | </wikitex> | ||
| − | == The | + | == The linking coefficient == |
| − | <wikitex>; | + | <wikitex>;\label{s:inv} |
| − | + | Here we define the linking coefficient and discuss its properties. | |
| − | + | Fix orientations of the standard spheres and balls. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | {{beginthm|Definition|(The linking coefficient)}}\label{dl} | |
| − | + | We define a map | |
| − | + | $$\lambda=\lambda_{12}:E^m(S^p\sqcup S^q)\to\pi_p(S^{m-q-1})\quad\text{for}\quad m\ge q+3.$$ | |
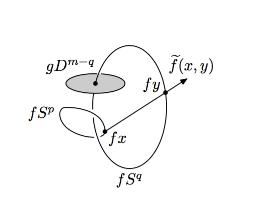
| − | + | Take an embedding $f:S^p\sqcup S^q\to S^m$ representing an element $[f]\in E^m(S^p\sqcup S^q)$. | |
| − | + | Take an embedding $g:D^{m-q}\to S^m$ such that $g(D^{m-q})$ intersects $f(S^q)$ transversely at exactly one point with positive sign; see Figure 4. | |
| − | + | [[Image:GaussMap-and-MeridianDisc.jpg|thumb|450px|Figure 4: The disc $gD^{m-q}$ and Gauss map $\widetilde f$]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | Take an embedding $g:D^{m-q}\to S^m$ such that $ | + | |
| − | + | ||
Then the restriction $h':S^{m-q-1}\to S^m-fS^q$ of $g$ to $\partial D^{m-q}$ is a homotopy equivalence. | Then the restriction $h':S^{m-q-1}\to S^m-fS^q$ of $g$ to $\partial D^{m-q}$ is a homotopy equivalence. | ||
| − | (Indeed, since $m\ge q+3$, the complement $S^m-fS^q$ is simply-connected. | + | (Indeed, since $m\ge q+3$, by general position the complement $S^m-fS^q$ is simply-connected. |
| − | By Alexander duality $h'$ induces isomorphism in homology. | + | By Alexander duality, $h'$ induces isomorphism in homology. |
| − | Hence by Hurewicz and Whitehead theorems $h'$ is a homotopy equivalence.) | + | Hence by the Hurewicz and Whitehead theorems $h'$ is a homotopy equivalence.) |
| − | + | ||
Let $h$ be a homotopy inverse of $h'$. | Let $h$ be a homotopy inverse of $h'$. | ||
Define | Define | ||
| − | $$\lambda | + | $$\lambda[f]=\lambda_{12}[f]:=[S^p\xrightarrow{~f|_{S^p}~} S^m-fS^q\overset h\to S^{m-q-1}]\in\pi_p(S^{m-q-1}).$$ |
| + | {{endthm}} | ||
{{beginthm|Remark}}\label{lkrem} | {{beginthm|Remark}}\label{lkrem} | ||
| − | (a) Clearly, $\lambda | + | (a) Clearly, $\lambda[f]$ is well-defined, i.e. is independent of the choices of $g,h',h$ and of the representative $f$ of $[f]$. |
| − | + | One can check that $\lambda$ is a homomorphism. | |
| − | (b) | + | (b) Analogously one can define $\lambda_{21}[f]\in\pi_q(S^{m-p-1})$ for $m\ge p+3$, by exchanging $p$ and $q$ in the above definition. |
| − | + | ||
| − | (c) | + | (c) Clearly, $\lambda\zeta=\id\pi_p(S^{m-q-1})$ for the [[#Examples|Zeeman map]] $\zeta$. So $\lambda$ is surjective and $\zeta$ is injective. |
| − | (d) | + | (d) For $m=p+q+1$ there is a simpler alternative definition using homological ideas. That definition can be generalized to the case where the components are closed orientable manifolds. Cf. [[Embeddings_just_below_the_stable_range:_classification#The_Whitney_invariant|Remark 5.3.f]] of \cite{Skopenkov2016e}. |
| − | + | {{endthm}} | |
| − | ( | + | Recall that by the Freudenthal Suspension Theorem the stable suspension homomorphism $\Sigma^{\infty}:\pi_p(S^{m-q-1})\to\pi^S_{p+q+1-m}$ is an isomorphism for $m\ge\frac p2+q+2$. The stable suspension of the linking coefficient can be described as follows. |
| − | + | ||
| + | {{beginthm|Definition|(The $\alpha$-invariant)}}\label{d:alpha} We define a map | ||
| + | $E^m(S^p\sqcup S^q)\to\pi^S_{p+q+1-m}$ for $p,q\le m-2$. | ||
| + | Take an embedding $f:S^p\sqcup S^q\to S^m$ representing an element $[f]\in E^m(S^p\sqcup S^q)$. | ||
| + | Define the Gauss map (see Figure 4) | ||
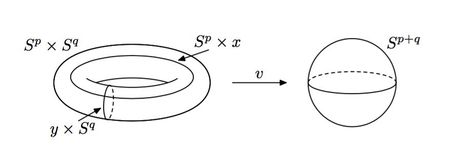
| + | $$\widetilde f:S^p\times S^q\to S^{m-1}\quad\text{by}\quad\widetilde f(x,y)=\frac{fx-fy}{|fx-fy|}.$$ | ||
| + | For $p,q\le m-2$ define the $\alpha$-invariant by | ||
| + | $$\alpha[f]=[\widetilde f]\in[S^p\times S^q,S^{m-1}]\overset{v^*}\cong\pi_{p+q}(S^{m-1})\cong\pi^S_{p+q+1-m}.$$ | ||
| + | The second isomorphism in this formula is the suspension isomorphism. | ||
| + | The map $v:S^p\times S^q\to\frac{S^p\times S^q}{S^p\vee S^q}\cong S^{p+q}$ is the quotient map, see Figure 5. | ||
| + | [[Image:33.jpg|thumb|450px|Figure 5: Contraction of the meridian and the parallel of the torus yield the sphere]] | ||
| + | The map $v^*$ is a 1--1 correspondence for $m\ge q+2$. | ||
| + | (For $m\ge q+3$ this follows by general position and for $m=q+2$ by the cofibration Barratt-Puppe exact sequence of pair $(S^p\times S^q,S^p\vee S^q)$ and by the existence of a retraction $\Sigma(S^p\times S^q)\to\Sigma(S^p\vee S^q)$.) | ||
| + | <!-- [[Media:33.pdf|figure 5]]. the example showing that MA does not display pdf figures: [[Image:33.pdf|thumb|450px|Figure 5]] --> | ||
{{endthm}} | {{endthm}} | ||
| − | + | One can easily check that $\alpha$ is well-defined and for $p,q\le m-3$ is a homomorphism. | |
| + | {{beginthm|Lemma|\cite[Lemma 5.1]{Kervaire1959a}}} | ||
| + | We have $\alpha=\pm\Sigma^{\infty}\lambda_{12}$ for $p,q\le m-3$. | ||
| + | {{endthm}} | ||
| + | |||
| + | Hence $\Sigma^{\infty}\lambda_{12}=\pm\Sigma^{\infty}\lambda_{21}$, even though in general $\lambda_{12} \neq \pm \lambda_{21}$ as we explain in Example \ref{belmetwhi}.a,c. | ||
| + | |||
| + | Note that the $\alpha$-invariant can be defined in more general situations \cite{Koschorke1988}, \cite[$\S$5]{Skopenkov2006}. | ||
| + | </wikitex> | ||
| + | |||
| + | == Classification in the metastable range == | ||
| + | <wikitex>; | ||
{{beginthm|The Haefliger-Zeeman Theorem}}\label{lkhaze} | {{beginthm|The Haefliger-Zeeman Theorem}}\label{lkhaze} | ||
| − | If $1\le p\le q$, then both $\lambda$ and $\ | + | If $1\le p\le q$, then both $\lambda$ and $\zeta$ are isomorphisms for $m\ge\frac{3q}2+2$ in the smooth category, and for $m\ge\frac p2+q+2$ in the PL category. |
| − | in the PL | + | |
{{endthm}} | {{endthm}} | ||
| − | The surjectivity of $\lambda$ ( | + | The surjectivity of $\lambda$ (or the injectivity of $\zeta$) follows from $\lambda\zeta=\id$. |
| − | The injectivity of $\lambda$ ( | + | The injectivity of $\lambda$ (or the surjectivity of $\zeta$) is proved in \cite[Theorem in $\S$5]{Haefliger1962t}, \cite{Zeeman1962} |
| − | (or follows from the Haefliger-Weber Theorem 5.4 and Deleted Product Lemma 5.3.a | + | (or follows from \cite[the Haefliger-Weber Theorem 5.4 and the Deleted Product Lemma 5.3.a]{Skopenkov2006}). |
| − | An analogue of this result holds for links with many components | + | An analogue of this result holds for links with many components, each of the same dimension \cite[Theorem in $\S$5]{Haefliger1962t}. Let $(q) = (q, \dots, q)$ be the $s$-tuple consisting entirely of some positive integer $q$. |
| − | + | ||
| − | + | {{beginthm|Theorem}}\label{t:lkmany} The collection of pairwise linking coefficients | |
| + | $$\bigoplus\limits_{1\le i<j\le s}\lambda_{ij} : E^m(S^{(q)}) \to (\pi_{2q+1-m}^S)^{s(s-1)/2}$$ | ||
| + | is a 1-1 correspondence for $m\ge\frac{3q}2+2$. | ||
| + | {{endthm}} | ||
| + | </wikitex> | ||
| − | + | ==Examples beyond the metastable range== | |
| − | + | <wikitex>;\label{s:ebmr} | |
| − | + | For $l=1$ the results of this section are parts of low-dimensional link theory, so they were known well before given references. | |
| − | For | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | First we present an example of the ''non-injectivity of the collection of pairwise linking coefficients'', which shows that the dimension restriction is sharp in Theorem \ref{t:lkmany}. | |
| − | + | ||
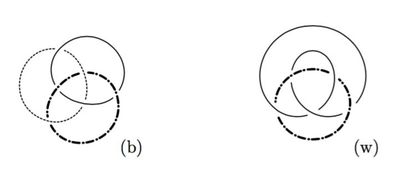
| − | + | {{beginthm|Example|(Borromean rings)}}\label{belmetbor} | |
| − | + | (a) There is a non-trivial embedding $S^{2l-1}\sqcup S^{2l-1}\sqcup S^{2l-1}\to\R^{3l}$ whose restriction to each 2-component sublink is trivial \cite[4.1]{Haefliger1962}, \cite[$\S$6]{Haefliger1962t}. | |
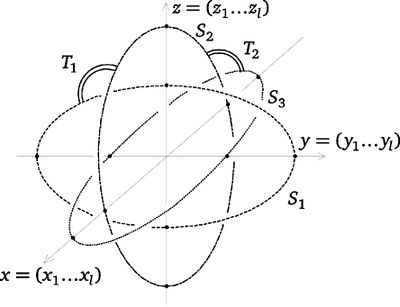
| − | + | In order to construct such an embedding, denote coordinates in $\Rr^{3l}$ by $(x,y,z)=(x_1,\dots,x_l,y_1,\dots,y_l,z_1,\dots,z_l)$. | |
| + | The (higher-dimensional) [[Wikipedia:Borromean_rings|`Borromean spheres']] are given by the following three systems of equations: | ||
| + | $$\left\{\begin{array}{c} x=0\\ |y|^2+2|z|^2=1,\end{array}\right. \qquad | ||
| + | \left\{\begin{array}{c} y=0\\ |z|^2+2|x|^2=1\end{array}\right. \qquad\text{and}\qquad \left\{\begin{array}{c} z=0\\ |x|^2+2|y|^2=1. \end{array}\right.$$ | ||
| + | [[Image:borromean_hidim_new.jpg|thumb|400px|Figure 6: The Borromean rings]] | ||
| + | See Figure 6. | ||
| + | The required embedding, called Borromean link, is any embedding whose image is the union of the Borromean spheres. | ||
| + | <!--See [[Media:35.pdf|the figure]] and [[Media:36.pdf|another figure]]. \cite[Figures 3.5 and 3.6]{Skopenkov2006} --> | ||
| + | |||
| + | (b) By moving two of the Borromean spheres and self-intersecting them, we can drag the remaining sphere far away from the two. | ||
| + | More precisely, each two of the Borromean spheres span two (intersecting) $2l$-disks disjoint from the remaining sphere. | ||
| + | |||
| + | (c) Restriction of the Borromean link to each 2-component sublink is trivial, because each two of the Borromean spheres span two disjoint $2l$-disks (intersecting the remaining sphere). | ||
| + | Moreover, we can take these $2l$-disks so that | ||
| + | |||
| + | * each one of them intersects the remaining sphere transversely by an $(l-1)$-sphere; | ||
| + | |||
| + | * the obtained two disjoint $(l-1)$-spheres in the remaining sphere have linking number $\pm1$, i.e. one of them spans an $l$-disk (in the remaining sphere) itersecting the other transversely at exacly one point. | ||
| + | |||
| + | (d) The Borromean link is distinguished from the standard embedding by ''triple linking number'' of Milnor-Haefliger-Steer-Massey defined as follows (cf. (c)). | ||
| + | Take a 3-component link, i.e. an embedding $g:S^{2l-1}_1\sqcup S^{2l-1}_2\sqcup S^{2l-1}_3\to S^{3l}$. | ||
| + | Assume that $g$ is ''pairwise unlinked'', i.e. every two components are contained in disjoint smooth balls. | ||
| + | Let $D_2,D_3\subset S^{3l}$ be disjoint oriented embedded $2l$-disks in general position to $g_1:=g|_{S^{2l-1}_1}$, and such that $g(S^{2l-1}_i)=\partial D_i$ for $i=2,3$. | ||
| + | Then for $j=2,3$ the preimage $g_1^{-1}D_j$ is an oriented $(l-1)$-submanifold of $S^{2l-1}_1$ missing $g_1^{-1}D_{5-j}$. | ||
| + | Let $\mu(g)$ be the linking number of $g_1^{-1}D_2$ and $g_1^{-1}D_3$ in $S^{2l-1}_1$. | ||
| + | |||
| + | (e) In a standard way one checks that the triple linking number is well-defined, i.e. is independent of the choice of $D_2,D_3$, and of the isotopy of $g$. | ||
| + | The above definition is equivalent to the standard definition of Milnor-Haefliger-Steer-Massey number \cite[$\S$4]{Haefliger1962t}, \cite{HaefligerSteer1965}, \cite[proof of Theorem 9.4]{Haefliger1966a}, \cite{Massey1968}, \cite[$\S$7]{Massey1990} by the well-known `linking number' definition of the Whitehead invariant $\pi_{2l-1}(S^l\vee S^l)\to\Z$ \cite[$\S$2, Sketch of a proof of (b1)]{Skopenkov2020e}. | ||
| + | If $g$ is pairwise unlinked, then the number $\mu$ is independent of permutation of the components, up to multiplication by $\pm1$ \cite{HaefligerSteer1965} (this can be easily proved directly). | ||
| + | |||
| + | (f) The Borromean link is non-trivial also because joining the three components with two tubes (i.e. `linked analogue' of [[High_codimension_embeddings#Embedded_connected_sum|embedded connected sum]] of the components \cite[$\S$4]{Skopenkov2016c}) yields a non-trivial knot \cite[Theorem 4.3]{Haefliger1962}, cf. [[3-manifolds_in_6-space#Examples|the Haefliger Trefoil knot]] \cite[Example 2.1]{Skopenkov2016t}. | ||
| + | {{endthm}} | ||
| + | |||
| + | Next we present an example of the ''non-injectivity of the linking coefficient'', which shows that the dimension restriction is sharp in Theorem \ref{lkhaze}. | ||
| + | |||
| + | {{beginthm|Example|(Whitehead link)}}\label{belmetwhi} (a) For every positive integer $l$ there is a non-trivial embedding $w:S^{2l-1}\sqcup S^{2l-1}\to\R^{3l}$ such that the second component is null-homotopic in the complement of the first component (i.e. the linking coefficient $\lambda_{21}(w)$ is trivial). | ||
| + | [[Image:Borromean-to-Whitehead.jpg|thumb|400px|Figure 7: The Borromean rings and Whitehead link for $l = 1$]] | ||
| + | |||
| + | Such an embedding is obtained from the Borromean rings embedding by joining the second and the third components with a tube, i.e. by the `linked analogue' of the [[Embeddings_just_below_the_stable_range:_classification#Embedded_connected_sum|embedded connected sum]] of the components \cite[$\S$3, $\S$4]{Skopenkov2016c}; see also the [[Wikipedia:Whitehead_link|Wikipedia article on the Whitehead link]]. (For $l=1$ the connected sum is not well-defined, so we take the specific connected sum (w) from Figure 7.) | ||
| + | |||
| + | (b) The second component is null-homotopic in the complement of the first component by Example \ref{belmetbor}.b. | ||
| + | |||
| + | (c) For $l\ne1,3,7$ the Whitehead link is non-trivial because the first component is not null-homotopic in the complement of the second component. | ||
| + | More precisely, $\lambda_{12}(w)$ equals to the Whitehead square $[\iota_l,\iota_l]\ne0$ of the generator $\iota_l\in\pi_l(S^l)$ \cite[end of $\S$6]{Haefliger1962t} (I do not know a written proof of this except \cite[the Whitehead link Lemma 2.14]{Skopenkov2015a} for $l$ even). | ||
| + | For $l=1,3,7$ the Whitehead link is distinguished from the standard embedding by more complicated Sato-Levine invariant \cite{Skopenkov2006a}. | ||
| + | |||
| + | (d) This example (in higher dimensions, i.e. for $l>1$) seems to have been discovered by Whitehead, in connection with Whitehead product. <!--It would be interesting to find a publication where it first appeared.--> | ||
| + | |||
| + | (e) For some results on links $S^{2l-1}\sqcup S^{2l-1}\to\R^{3l}$ related to the Whitehead link see \cite[$\S$2.5]{Skopenkov2015a}. | ||
| + | {{endthm}} | ||
</wikitex> | </wikitex> | ||
| − | == | + | == Linked manifolds == |
<wikitex>; | <wikitex>; | ||
| + | In this section we state some analogues of Theorem \ref{t:lkmany} where spheres are replaced by general manifolds. We start with a simple case where no high-connectivity assumptions are made on the source manifolds. | ||
| − | + | {{beginthm|Theorem}}\label{t:man} Assume that $N_1,\ldots,N_s$ are closed connected manifolds and $\frac{m-1}2=\dim N_i\ge2$ for every $i$. Then for an embedding $f:N_1\sqcup\ldots\sqcup N_s\to\Rr^m$ and every $1\le i<j\le s$ one defines the linking coefficient $\lambda_{ij}(f)$, see Remark \ref{lkrem}.e. We have $\lambda_{ij}(f)\in\Z$ if both $N_i$ and $N_j$ are orientable, and $\lambda_{ij}(f)\in\Z_2$ otherwise. Then the collection of pairwise linking coefficients | |
| − | + | $$\bigoplus\limits_{1\le i<j\le s}\lambda_{ij} : | |
| − | + | E^m(N_1\sqcup\ldots\sqcup N_s) \to \Z^{\frac{t(t-1)}2} \oplus \Z_2^{\frac{s(s-1)}2-\frac{t(t-1)}2}$$ | |
| − | {{beginthm| | + | is well-defined and is a 1-1 correspondence, where $t$ of $N_1,\ldots, N_s$ are orientable and $s-t$ |
| − | + | are not. | |
| − | + | ||
| − | \ | + | |
{{endthm}} | {{endthm}} | ||
| − | + | We present the general case of the classification of embeddings of disjoint highly-connected manifolds only for the case of two oriented components of the same dimension. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | {{beginthm|Theorem}}\label{t:mang} Let $N_1$ and $N_2$ be closed $n$-dimensional homologically $(2n-m+1)$-connected orientable manifolds. For an embedding $f:N_1\sqcup N_2\to\Rr^m$ one can define the invariant $\alpha(f)\in\pi_{2n-m+1}^S$ analogously to Definition \ref{d:alpha}. Then | |
| + | $$\alpha:E^m(N_1\sqcup N_2)\to\pi_{2n-m+1}^S$$ | ||
| + | is well-defined and is a 1-1 correspondence, provided $2m\ge3n+4$. | ||
| + | {{endthm}} | ||
| − | + | Theorems \ref{t:man} and \ref{t:mang} are easily deduced from the Zeeman/Haefliger Unknotting Theorem in the PL/smooth category \cite{Ivansic&Horvatic1974}. They are also corollaries of \cite[the Haefliger-Weber Theorem 5.4]{Skopenkov2006} (in both categories); the calculations are analogous to the construction of the 1-1 correspondence $[S^p\times S^q,S^{m-1}]\to\pi^S_{p+q+1-m}$ in Definition \ref{d:alpha}. | |
| + | See \cite[Proposition 1.2]{Skopenkov2000} for the ''link map'' analogue. | ||
| − | { | + | Now we present an extension of Theorems \ref{t:man} and \ref{t:mang} to a case where $m = 6$ and $n = 3$. In particular, for the results below $m=2\dim N_i$, $2m=3n+3$ |
| − | is a | + | and the manifolds $N_i$ are only $(2n-m)$-connected. An embedding $(S^2\times S^1)\sqcup S^3\to\Rr^6$ is ''Brunnian'' if its restriction to each component is isotopic to the standard embedding. <!--For any triple of integers $k,l,n$ such that $l-n$ is even, one can explicitly construct \cite{Avvakumov2016} a Brunnian embedding $f_{k,l,n}:(S^2\times S^1)\sqcup S^3\to\Rr^6$ so that the following theorem holds. --> For each triple of integers $k,l,n$ such that $l-n$ is even, Avvakumov has constructed a Brunnian embedding $f_{k,l,n}:(S^2\times S^1)\sqcup S^3\to\Rr^6$, which appears in the next result \cite[$\S$1]{Avvakumov2016}. |
| + | |||
| + | {{beginthm|Theorem}}\label{t:avv} \cite[Theorem 1]{Avvakumov2016} | ||
| + | Any Brunnian embedding $(S^2\times S^1)\sqcup S^3\to\Rr^6$ is isotopic to $f_{k,l,n}$ for some integers $k,l,n$ such that $l-n$ is even. Two embeddings $f_{k,l,n}$ and $f_{k',l',n'}$ are isotopic if and only if $k=k'$ and both $l-l'$ and $n-n'$ are divisible by $2k$. | ||
{{endthm}} | {{endthm}} | ||
| − | The | + | The proof uses M. Skopenkov's classification of embeddings $S^3\sqcup S^3\to\Rr^6$ (Theorem \ref{belmethae} for $m=2p=2q=6$). The following corollary shows that the relation between the embeddings $(S^2\times S^1)\sqcup S^3\to\Rr^6$ and $S^3\sqcup S^3\to\Rr^6$ is not trivial. |
| − | + | ||
| − | + | {{beginthm|Corollary}}\label{c:avv} \cite[Corollary 1]{Avvakumov2016}, cf. \cite[Corollary 3.5.b]{Skopenkov2016t} | |
| − | + | There exist embeddings $f:(S^2\times S^1)\sqcup S^3\to\Rr^6$ and $g,g':S^3\sqcup S^3\to\Rr^6$ such that the componentwise embedded connected sum $f\#g$ is isotopic to $f\#g'$ but $g$ is not isotopic to $g'$. | |
| − | + | {{endthm}} | |
| − | \ | + | |
| + | For an unpublished generalization of Theorem \ref{t:avv} and Corollary \ref{c:avv} see \cite{Avvakumov2017}. | ||
| + | </wikitex> | ||
| + | |||
| + | == Reduction to the case with unknotted components == | ||
| + | <wikitex>; | ||
| + | In this section we assume that $(n)$ is an $s$-tuple such that $m\ge n_i+3$. | ||
| − | + | Define $E^m_U(S^{(n)}) \subset E^m_D(S^{(n)})$ to be the subgroup of links all whose components are unknotted, i.e. isotopic to the standard embedding $S^{n_i} \to S^m$. We remark that $E^m_U(S^{(n)})\cong E^m_{PL}(S^{(n)})$ \cite[$\S\S$ 2.4, 2.6 and 9.3]{Haefliger1966a}, \cite[$\S$1.5]{Crowley&Ferry&Skopenkov2011}. | |
| − | + | Define the restriction homomorphism by mapping the isotopy class of a link to the ordered $s$-tuple of the isotopy classes of its components: | |
| − | + | $$ r \colon E^m_D(S^{(n)}) \to \bigoplus_{i=1}^s E^m_D(S^{n_i}), \quad r[f]:=\oplus_{i=1}^s [f|_{S^{n_i}} \colon S^{n_i} \to S^m].$$ | |
| − | + | Take $s$ pairwise disjoint $m$-discs in $S^m$, i.e. take an embedding $g:D^m_1\sqcup\ldots\sqcup D^m_s\to S^m$. Define | |
| − | ==== | + | $$j \colon \bigoplus_{i=1}^s E^m_D(S^{n_i}) \to E^m_D(S^{(n)})\quad\text{by}\quad j([f_1], \ldots, [f_s]):=[(g\circ\sqcup_{i=1}^s f_i):S^{(n)}\to S^m].$$ |
| + | Then $j$ is a right inverse of the restriction homomorphism $r$, i.e. $r\circ j=\mathrm{id}$. | ||
| + | The unknotting homomorphism $u$ is defined to be the homomorphism | ||
| + | $$ u = \mathrm{id} - j \circ r \colon E^m_D(S^{(n)}) \to E^m_U(S^{(n)}).$$ | ||
| + | Informally, the homomorphism $u$ is obtained by taking embedded connected sums of components with knots $h_i:S^{n_i}\to S^m$ representing the elements of $E^m_D(S^{n_i})$ inverse to the components, whose images $h_i(S^{n_i})$ are small and are close to the components. | ||
| + | |||
| + | {{beginthm|Theorem}}\label{dpl} \cite[Theorem 2.4]{Haefliger1966a} For $n_1,\ldots,n_s\le m-3$, the homomorphism | ||
| + | $$u \oplus r \colon E^m_D(S^{(n)}) \to E^m_U(S^{(n)})\oplus \bigoplus_{i=1}^s E^m_D(S^{n_i})$$ | ||
| + | is an isomorphism. | ||
| + | {{endthm}} | ||
| − | + | For [[Knots,_i.e._embeddings_of_spheres|some information on the groups $E^m_D(S^q)$]] see \cite{Skopenkov2016s}, \cite[$\S$3.3]{Skopenkov2006}. | |
| − | + | </wikitex> | |
| − | + | ||
| − | {{beginthm| | + | ==Classification beyond the metastable range== |
| − | + | <wikitex>;\label{s:cbmr} | |
| − | + | ||
| − | + | {{beginthm|Theorem}}\label{belmethae} | |
| − | If $p\le q\le m-3$ and $3m\ge2p+2q+6$, then there is a | + | \cite[Theorem 10.7]{Haefliger1966a}, \cite[Theorem 1.1]{Skopenkov2009}, \cite[Theorem 1.1]{Skopenkov2006b} |
| − | $$\lambda_{12}\oplus\ | + | If $p\le q\le m-3$ and $3m\ge2p+2q+6$, then there is a homomorphism $\beta$ for which the following map is an isomorphism |
| + | $$\lambda_{12}\oplus\beta:E^m_{PL}(S^p\sqcup S^q)\to\pi_p(S^{m-q-1})\oplus \pi_{p+q+2-m}(SO, SO_{m-p-1}).$$ | ||
{{endthm}} | {{endthm}} | ||
| − | The map $\ | + | The map $\beta$ and its right inverse $\pi_{p+q+2-m}(SO, SO_{m-p-1})\to\ker\lambda_{12}$ are constructed in \cite[$\S$10]{Haefliger1966a} and in \cite[8.13]{Haefliger1966}, respectively. For alternative geometric (and presumably equivalent) definitions of $\beta$ see \cite[$\S$3]{Skopenkov2009}, \cite[$\S$5]{Skopenkov2006b}, cf. \cite[$\S$2]{Skopenkov2007} and \cite[$\S$2.3]{Crowley&Skopenkov2016}. For a historical remark see \cite[the second paragraph in p. 2]{Skopenkov2009}. |
| + | <!--The case $3m\ge4q+6$ (when by general position no quadruple linking appears) is called a `2-metastable range' for embeddings of $q$-polyhdera in $\R^m$. --> | ||
| − | + | {{beginthm|Remark}}\label{r:bel} | |
| − | $$E^{3l}_{PL}(S^{2l-1}\sqcup S^{2l-1})\ | + | (a) Theorem \ref{belmethae} implies that for any $l\ge2$ we have an isomorphism |
| − | + | $$\lambda_{12}\oplus\beta:E^{3l}_{PL}(S^{2l-1}\sqcup S^{2l-1})\to\pi_{2l-1}(S^l)\oplus\Z_{\varepsilon(l)}.$$ | |
| − | $$\lambda_{12}\oplus\lambda_{21}:E^{3l}_{PL}(S^{2l-1}\sqcup S^{2l-1})\to\pi_{2l-1}(S^l)\oplus\pi_{2l-1}(S^l) | + | |
| − | + | (b) For any $l\not\in\{1,3,7\}$, the map | |
| − | \cite{ | + | $$\lambda_{12}\oplus\lambda_{21}:E^{3l}_{PL}(S^{2l-1}\sqcup S^{2l-1})\to\pi_{2l-1}(S^l)\oplus\pi_{2l-1}(S^l)$$ |
| − | + | is injective and its image is $\{(a,b)\ :\ \Sigma(a+(-1)^lb)=0\}$. | |
| + | |||
| + | For $l\ge4$ see \cite[$\S$6]{Haefliger1962t}. The following proof for $l=2$ and general remark are intended for specialists. | ||
| + | |||
| + | For $l=2$ there is an exact sequence $\pi_5(S^3) \to \ker \lambda_{12} \xrightarrow{\lambda_{21}|_{ \ker \lambda_{12} } } \pi_3(S^2) \xrightarrow{\Sigma} \pi_4(S^3)$, | ||
| + | where $\lambda_{12}$ is $\lambda_{12,PL}$ <!-- not $\lambda_{12,D}$ --> \cite[Corollary 10.3]{Haefliger1966a}. | ||
| + | We have $\pi_3(S^2)\cong\Zz$, $\pi_4(S^3)\cong\Zz_2$ and $\Sigma$ is the reduction modulo 2. | ||
| + | By the exactness of the previous sequence, <!--$\text{im} \, \lambda_{21}= 2\Z$. --> $ \lambda_{21}(\ker \lambda_{12}) = 2\Z$. | ||
| + | By (a) $\ker \lambda_{12} \cong \Z$. | ||
| + | Hence $\lambda_{21}|_{\ker\lambda_{12}}$ is injective. | ||
| + | We have $\Sigma\lambda_{21}=\Sigma\lambda_{12}$ by \cite[Proposition 10.2]{Haefliger1966a}. | ||
| + | So the formula of (b) follows. | ||
| + | |||
| + | Analogously to \cite[Theorem 3.5]{Skopenkov2009} using geometric definitons of $\beta$ \cite[$\S$3]{Skopenkov2009}, \cite[$\S$5]{Skopenkov2006b} and geomeric interpretation of the EHP sequence $\ldots\overset H\to\pi_l(SO,SO_l)\overset P\to\pi_{2l-1}(S^l)\overset\Sigma\to\pi_{l-1}^S\overset H\to\ldots$ \cite[Main Theorem in $\S$1]{Koschorke&Sanderson1977} one can possibly prove that $\pm P\beta=\lambda_{12}+(-1)^l\lambda_{21}$. Then (b) would follow. | ||
| + | |||
| + | (c) For any $l\in\{1,3,7\}$ the map $\lambda_{12}\oplus\lambda_{21}$ in (b) above is not injective \cite[$\S$6]{Haefliger1962t}. | ||
| + | {{endthm}} | ||
| + | |||
| + | {{beginthm|Theorem}}\label{three} | ||
| + | For any $l>2$ there an isomorphism | ||
| + | $$E^{3l}_{PL}(S^{2l-1}\sqcup S^{2l-1}\sqcup S^{2l-1})\to\pi_{2l-1}(S^l)^3\oplus\Z_{\varepsilon(l)}^3\oplus\Z$$ | ||
| + | which is the sum of 3 pairwise invariants of Remark \ref{r:bel}.a, and the triple linking number ($\S$\ref{s:ebmr}). | ||
| + | {{endthm}} | ||
| + | |||
| + | This follows from \cite[Theorem 9.4]{Haefliger1966a}, see also \cite[$\S$6]{Haefliger1962t}. | ||
</wikitex> | </wikitex> | ||
| − | == | + | == Classification in codimension at least 3 == |
| − | <wikitex>; | + | <wikitex>;\label{s:cl3} |
| − | + | In this section we assume that $(n)$ is an $s$-tuple such that $m\ge n_i+3$. | |
| − | + | For this case a readily calculable classification of $E^m_{PL}(S^{(n)})\otimes\Qq$ was obtained in | |
| − | \ | + | \cite[Theorem 1.9]{Crowley&Ferry&Skopenkov2011}. In particular, \cite[$\S$1.2]{Crowley&Ferry&Skopenkov2011} contains necessary and sufficient conditions on $(n)$ which determine when $E^m_{PL}(S^{(n)})$ is finite. These results are elementary, but the precise formulations are technical. Hence, we only state the following corollary of \cite[Theorem 1.9 and $\S$1.2]{Crowley&Ferry&Skopenkov2011} and describe the methods of its proof in Definition \ref{d:hclink} and Theorem \ref{thm:hclink} below. |
| + | <!--, as well as an effective procedure for computing the rank of the group $E^m_{PL}(S^{(n)})$.--> | ||
| + | |||
| + | {{beginthm|Theorem}}\label{t:cfs} There are algorithms which for integers $m,n_1,\ldots,n_s>0$ | ||
| + | |||
| + | (a) calculate ${\rm rk}E^m_{PL}(S^{(n)})$. | ||
| + | |||
| + | (b) determine whether $E^m_{PL}(S^{(n)})$ is finite. | ||
| + | {{endthm}} | ||
| + | |||
| + | {{beginthm|Definition|(The Haefliger link sequence)}}\label{d:hclink} | ||
| + | In \cite[1.2-1.5]{Haefliger1966a} Haefliger defined a long exact sequence of abelian groups | ||
| + | $$ \ldots \to \Pi_{m-1}^{(n)} \xrightarrow{~\mu~} E^m_{PL}(S^{(n)}) \xrightarrow{~\lambda~} \oplus_{j=1}^s \ker p_{n_j,j} \xrightarrow{~w~} \Pi_{m-2}^{(n-1)} \xrightarrow{~\mu~} E^{m-1}_{PL}(S^{(n-1)})\to \ldots~.$$ | ||
| + | We briefly define the groups and homomorphisms in this sequence, refering to \cite[1.4]{Haefliger1966a} for details. | ||
| + | We first note that in the sequence above the $s$-tuples $m-n_1,\ldots,m-n_s$ are the same for different terms. | ||
| + | Denote $W :=\vee_{i=1}^s S^{m-n_i-1}$. | ||
| + | For any $j=1,\ldots,s$ and positive integer $k$ denote by $p_{k,j}\colon\pi_k(W)\to\pi_k(S^{m-n_j-1})$ the homomorphism induced by the collapse map onto to the $j$-component of the wedge. Denote $(n-1):=(n_1 -1, \ldots, n_s-1)$ and $\Pi_{m-1}^{(n)}:=\ker(\oplus_{i=1}^s p_{m-1,i})\subset\pi_{m-1}(W)$. | ||
| + | |||
| + | It can be shown that each component of a link $f:S^{(n)} \to S^m$ has a non-zero normal vector field. So each component of a link can be pushed off along such a vector field into the complement $C_f$. Analogously to Definition \ref{dl} there is a canonical homotopy equivalence $C_f \sim W$. It can also be shown that the homotopy class in $C_f$ of the push off of the $j$th component gives a well-defined map $\lambda_j:E^m_{PL}(S^{(n)})\to\ker p_{n_j,j}$. In fact, the map $\lambda_j$ is a generalization of the linking coefficient. Finally, define $\lambda:= \oplus_{j=1}^s \lambda_j$. | ||
| + | |||
| + | Taking the Whitehead product with the class of the inclusion of $S^{m-n_j-1}$ into $W$ defines a homomorphism $w_j \colon \ker p_{n_j,j}\to \Pi_{m-2}^{(n-1)}$. Define $w:=\oplus_{j=1}^s w_j$. | ||
| + | |||
| + | The definition of the homomorphism $\mu$ is given in \cite[1.5]{Haefliger1966a}. | ||
| + | {{endthm}} | ||
| + | |||
| + | {{beginthm|Theorem}}\label{thm:hclink} | ||
| + | (a) \cite[Theorem 1.3]{Haefliger1966a} The Haefliger link sequence is exact. | ||
| + | |||
| + | (b) The map $\lambda\otimes\Qq \colon E^m_{PL}(S^{(n)})\otimes\Qq \to \ker(w\otimes\Qq)$ is an isomorphism. | ||
| + | {{endthm}} | ||
| + | |||
| + | Part (b) follows because $\mu \otimes \Qq = 0$ \cite[Lemma 1.3]{Crowley&Ferry&Skopenkov2011}, and so the Haefliger link sequence after tensoring with the rational numbers $\Qq$ splits into short exact sequences. | ||
| − | + | In general, the computation of the groups and homomorphisms appearing in Theorem \ref{thm:hclink} is difficult. For (a) no computations are known except for those giving (b) and those giving Theorem \ref{belmethae} for $3m\ge2p+2q+7$ (note that Theorem \ref{belmethae} has a direct proof easier than proof of Theorem \ref{thm:hclink}.a). For (b) the computations constitute most of \cite{Crowley&Ferry&Skopenkov2011}. Hence Theorem \ref{thm:hclink} is not a readily calculable classification in general. <!-- $$ 0 \to E^m_{PL}(S^n) \otimes \Qq \xrightarrow{~\lambda \otimes \Qq~} (\oplus_{j=1}^s \mathop{Ker} p_{n_j,j}) \otimes \Qq \xrightarrow{~w \otimes \Qq~} \Pi^{m-2}_{n-1}\otimes \Qq \to 0.$$--> | |
</wikitex> | </wikitex> | ||
| − | |||
| − | |||
| − | |||
== References == | == References == | ||
Revision as of 21:01, 5 April 2024
| This page has been accepted for publication in the Bulletin of the Manifold Atlas. |
|
The user responsible for this page is Askopenkov. No other user may edit this page at present. |
1 Introduction
Most of this page is intended not only for specialists in embeddings, but also for mathematician from other areas who want to apply or to learn the theory of embeddings.
On this page we describe readily calculable classifications of embeddings of closed disconnected manifolds into  up to isotopy, and more generally of spaces which are a disjoint union of manifolds of varying dimensions. The presently known cases of such classifications are embeddings
up to isotopy, and more generally of spaces which are a disjoint union of manifolds of varying dimensions. The presently known cases of such classifications are embeddings 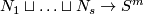 , where
, where 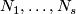 are spheres (or even closed manifolds) and
are spheres (or even closed manifolds) and 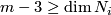 for every
for every  , under some further restrictions. For a related classification of knotted tori see [Skopenkov2016k].
, under some further restrictions. For a related classification of knotted tori see [Skopenkov2016k].
For an  -tuple
-tuple 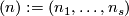 denote
denote 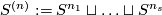 . Although
. Although 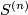 is not a manifold when
is not a manifold when 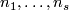 are not all equal, embeddings
are not all equal, embeddings 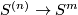 and isotopy between such embeddings are defined analogously to the case of manifolds [Skopenkov2016i]. Denote by
and isotopy between such embeddings are defined analogously to the case of manifolds [Skopenkov2016i]. Denote by 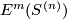 the set of embeddings
the set of embeddings 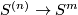 up to isotopy.
up to isotopy.
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3].
3].
The following table was obtained by Zeeman around 1960 (see the Haefliger-Zeeman Theorem 4.1 below):
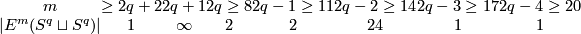
A component-wise version of embedded connected sum [Skopenkov2016c,  5] defines a commutative group structure on the set
5] defines a commutative group structure on the set 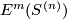 for
for 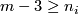 [Haefliger1966a, 2.5], [Skopenkov2015, Group Structure Lemma 2.2 and Remark 2.3.a], [Avvakumov2016,
[Haefliger1966a, 2.5], [Skopenkov2015, Group Structure Lemma 2.2 and Remark 2.3.a], [Avvakumov2016,  1], [Avvakumov2017,
1], [Avvakumov2017,  1.4], see Figure 1.
1.4], see Figure 1.
The standard embedding 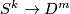 is defined by
is defined by 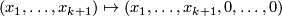 . Fix
. Fix  pairwise disjoint
pairwise disjoint  -discs
-discs 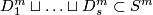 . The standard embedding
. The standard embedding 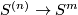 is defined by taking the union of the compositions of the standard embeddings
is defined by taking the union of the compositions of the standard embeddings 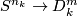 with the fixed inclusions
with the fixed inclusions 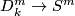 .
.
2 Examples
Recall that for any  -manifold
-manifold  and
and 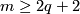 , every two embeddings
, every two embeddings 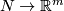 are isotopic [Skopenkov2016c, General Position Theorem 2.1], [Skopenkov2006, General Position Theorem 2.1].
The following example shows that the restriction
are isotopic [Skopenkov2016c, General Position Theorem 2.1], [Skopenkov2006, General Position Theorem 2.1].
The following example shows that the restriction 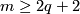 is sharp for non-connected manifolds.
is sharp for non-connected manifolds.
Example 2.1 (The Hopf Link).
(a) For every positive integer  there is an embedding
there is an embedding 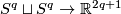 , which is not isotopic to the standard embedding.
, which is not isotopic to the standard embedding.
For 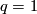 the Hopf link is shown in Figure 2. For all
the Hopf link is shown in Figure 2. For all  the image of the Hopf link is the union of two
the image of the Hopf link is the union of two  -spheres which can be described as follows:
-spheres which can be described as follows:
- either the spheres are
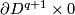 and
and 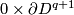 in
in 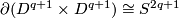 ;
;
- or they are given as the sets of points in
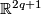 satisfying the following equations:
satisfying the following equations:
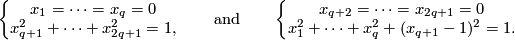
This embedding is distinguished from the standard embedding by the linking number (cf.  3).
3).
(b) For any 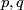 there is an embedding
there is an embedding 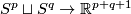 which is not isotopic to the standard embedding.
which is not isotopic to the standard embedding.
Analogously to (a), the image is the union of two spheres which can be described as follows:
- either the spheres are
 and
and 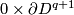 in
in 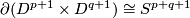 .
.
- or they are given as the points in
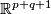 satisfying the following equations:
satisfying the following equations:
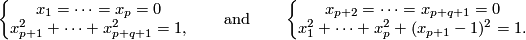
This embedding is also distinguished from the standard embedding by the linking number (cf.  3).
3).
Definition 2.2 (A link with prescribed linking coefficient). We define the `Zeeman' map
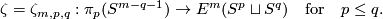
For a map 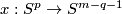 representing an element of
representing an element of 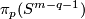 let
let
Tex syntax error
Tex syntax error. Let
Tex syntax error.
One can easily check that 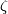 is well-defined and is a homomorphism.
is well-defined and is a homomorphism.
3 The linking coefficient
Here we define the linking coefficient and discuss its properties. Fix orientations of the standard spheres and balls.
Definition 3.1 (The linking coefficient). We define a map
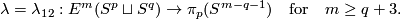
Take an embedding 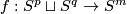 representing an element
representing an element ![[f]\in E^m(S^p\sqcup S^q)](/images/math/9/5/8/958e4adb33de7e2445e035db1cbd05a0.png) .
Take an embedding
.
Take an embedding 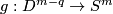 such that
such that 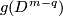 intersects
intersects 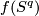 transversely at exactly one point with positive sign; see Figure 4.
transversely at exactly one point with positive sign; see Figure 4.
Then the restriction 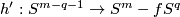 of
of  to
to 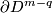 is a homotopy equivalence.
is a homotopy equivalence.
(Indeed, since 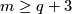 , by general position the complement
, by general position the complement 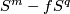 is simply-connected.
By Alexander duality,
is simply-connected.
By Alexander duality, 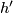 induces isomorphism in homology.
Hence by the Hurewicz and Whitehead theorems
induces isomorphism in homology.
Hence by the Hurewicz and Whitehead theorems 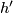 is a homotopy equivalence.)
is a homotopy equivalence.)
Let  be a homotopy inverse of
be a homotopy inverse of 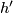 .
Define
.
Define
![\displaystyle \lambda[f]=\lambda_{12}[f]:=[S^p\xrightarrow{~f|_{S^p}~} S^m-fS^q\overset h\to S^{m-q-1}]\in\pi_p(S^{m-q-1}).](/images/math/7/0/2/702421c61c119e9f17cfea8b085f374a.png)
Remark 3.2.
(a) Clearly, ![\lambda[f]](/images/math/4/6/0/4603ad5fae840a15ed28fd021825efae.png) is well-defined, i.e. is independent of the choices of
is well-defined, i.e. is independent of the choices of 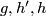 and of the representative
and of the representative  of
of ![[f]](/images/math/d/d/4/dd43b82529dd8d403c1585c5d151a163.png) .
One can check that
.
One can check that  is a homomorphism.
is a homomorphism.
(b) Analogously one can define ![\lambda_{21}[f]\in\pi_q(S^{m-p-1})](/images/math/5/b/8/5b81499fd01f4267c2347d2439817f40.png) for
for 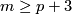 , by exchanging
, by exchanging  and
and  in the above definition.
in the above definition.
(c) Clearly, 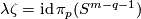 for the Zeeman map
for the Zeeman map 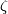 . So
. So  is surjective and
is surjective and 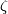 is injective.
is injective.
(d) For 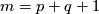 there is a simpler alternative definition using homological ideas. That definition can be generalized to the case where the components are closed orientable manifolds. Cf. Remark 5.3.f of [Skopenkov2016e].
there is a simpler alternative definition using homological ideas. That definition can be generalized to the case where the components are closed orientable manifolds. Cf. Remark 5.3.f of [Skopenkov2016e].
Recall that by the Freudenthal Suspension Theorem the stable suspension homomorphism 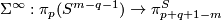 is an isomorphism for
is an isomorphism for 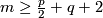 . The stable suspension of the linking coefficient can be described as follows.
. The stable suspension of the linking coefficient can be described as follows.
Definition 3.3 (The  -invariant). We define a map
-invariant). We define a map
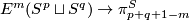 for
for 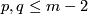 .
Take an embedding
.
Take an embedding 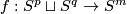 representing an element
representing an element ![[f]\in E^m(S^p\sqcup S^q)](/images/math/9/5/8/958e4adb33de7e2445e035db1cbd05a0.png) .
Define the Gauss map (see Figure 4)
.
Define the Gauss map (see Figure 4)
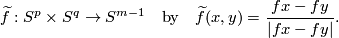
For 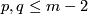 define the
define the  -invariant by
-invariant by
![\displaystyle \alpha[f]=[\widetilde f]\in[S^p\times S^q,S^{m-1}]\overset{v^*}\cong\pi_{p+q}(S^{m-1})\cong\pi^S_{p+q+1-m}.](/images/math/5/3/d/53debfbd4a5d88f0c6d79b4fce1d64a3.png)
The second isomorphism in this formula is the suspension isomorphism.
The map 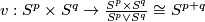 is the quotient map, see Figure 5.
is the quotient map, see Figure 5.
The map 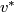 is a 1--1 correspondence for
is a 1--1 correspondence for 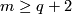 .
(For
.
(For 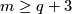 this follows by general position and for
this follows by general position and for 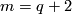 by the cofibration Barratt-Puppe exact sequence of pair
by the cofibration Barratt-Puppe exact sequence of pair 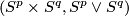 and by the existence of a retraction
and by the existence of a retraction 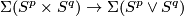 .)
.)
One can easily check that  is well-defined and for
is well-defined and for 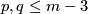 is a homomorphism.
is a homomorphism.
Lemma 3.4 [Kervaire1959a, Lemma 5.1].
We have 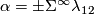 for
for 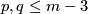 .
.
Hence 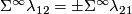 , even though in general
, even though in general 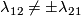 as we explain in Example 5.2.a,c.
as we explain in Example 5.2.a,c.
Note that the  -invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006,
-invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006,  5].
5].
4 Classification in the metastable range
The Haefliger-Zeeman Theorem 4.1.
If 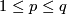 , then both
, then both  and
and 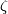 are isomorphisms for
are isomorphisms for 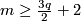 in the smooth category, and for
in the smooth category, and for 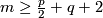 in the PL category.
in the PL category.
The surjectivity of  (or the injectivity of
(or the injectivity of 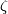 ) follows from
) follows from 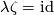 .
The injectivity of
.
The injectivity of  (or the surjectivity of
(or the surjectivity of 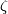 ) is proved in [Haefliger1962t, Theorem in
) is proved in [Haefliger1962t, Theorem in  5], [Zeeman1962]
(or follows from [Skopenkov2006, the Haefliger-Weber Theorem 5.4 and the Deleted Product Lemma 5.3.a]).
5], [Zeeman1962]
(or follows from [Skopenkov2006, the Haefliger-Weber Theorem 5.4 and the Deleted Product Lemma 5.3.a]).
An analogue of this result holds for links with many components, each of the same dimension [Haefliger1962t, Theorem in  5]. Let
5]. Let 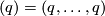 be the
be the  -tuple consisting entirely of some positive integer
-tuple consisting entirely of some positive integer  .
.
Theorem 4.2. The collection of pairwise linking coefficients
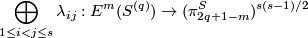
is a 1-1 correspondence for 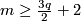 .
.
5 Examples beyond the metastable range
For 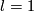 the results of this section are parts of low-dimensional link theory, so they were known well before given references.
the results of this section are parts of low-dimensional link theory, so they were known well before given references.
First we present an example of the non-injectivity of the collection of pairwise linking coefficients, which shows that the dimension restriction is sharp in Theorem 4.2.
Example 5.1 (Borromean rings).
(a) There is a non-trivial embedding 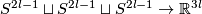 whose restriction to each 2-component sublink is trivial [Haefliger1962, 4.1], [Haefliger1962t,
whose restriction to each 2-component sublink is trivial [Haefliger1962, 4.1], [Haefliger1962t,  6].
6].
In order to construct such an embedding, denote coordinates in 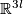 by
by 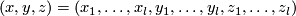 .
The (higher-dimensional) `Borromean spheres' are given by the following three systems of equations:
.
The (higher-dimensional) `Borromean spheres' are given by the following three systems of equations:
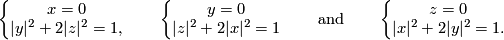
See Figure 6. The required embedding, called Borromean link, is any embedding whose image is the union of the Borromean spheres.
(b) By moving two of the Borromean spheres and self-intersecting them, we can drag the remaining sphere far away from the two.
More precisely, each two of the Borromean spheres span two (intersecting) 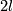 -disks disjoint from the remaining sphere.
-disks disjoint from the remaining sphere.
(c) Restriction of the Borromean link to each 2-component sublink is trivial, because each two of the Borromean spheres span two disjoint 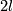 -disks (intersecting the remaining sphere).
Moreover, we can take these
-disks (intersecting the remaining sphere).
Moreover, we can take these 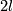 -disks so that
-disks so that
- each one of them intersects the remaining sphere transversely by an
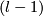 -sphere;
-sphere;
- the obtained two disjoint
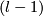 -spheres in the remaining sphere have linking number
-spheres in the remaining sphere have linking number 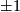 , i.e. one of them spans an
, i.e. one of them spans an  -disk (in the remaining sphere) itersecting the other transversely at exacly one point.
-disk (in the remaining sphere) itersecting the other transversely at exacly one point.
(d) The Borromean link is distinguished from the standard embedding by triple linking number of Milnor-Haefliger-Steer-Massey defined as follows (cf. (c)).
Take a 3-component link, i.e. an embedding 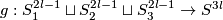 .
Assume that
.
Assume that  is pairwise unlinked, i.e. every two components are contained in disjoint smooth balls.
Let
is pairwise unlinked, i.e. every two components are contained in disjoint smooth balls.
Let 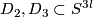 be disjoint oriented embedded
be disjoint oriented embedded 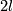 -disks in general position to
-disks in general position to 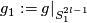 , and such that
, and such that 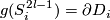 for
for 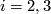 .
Then for
.
Then for 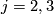 the preimage
the preimage 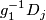 is an oriented
is an oriented 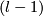 -submanifold of
-submanifold of 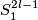 missing
missing 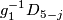 .
Let
.
Let 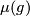 be the linking number of
be the linking number of 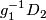 and
and 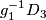 in
in 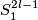 .
.
(e) In a standard way one checks that the triple linking number is well-defined, i.e. is independent of the choice of 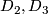 , and of the isotopy of
, and of the isotopy of  .
The above definition is equivalent to the standard definition of Milnor-Haefliger-Steer-Massey number [Haefliger1962t,
.
The above definition is equivalent to the standard definition of Milnor-Haefliger-Steer-Massey number [Haefliger1962t,  4], [HaefligerSteer1965], [Haefliger1966a, proof of Theorem 9.4], [Massey1968], [Massey1990,
4], [HaefligerSteer1965], [Haefliger1966a, proof of Theorem 9.4], [Massey1968], [Massey1990,  7] by the well-known `linking number' definition of the Whitehead invariant
7] by the well-known `linking number' definition of the Whitehead invariant 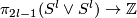 [Skopenkov2020e,
[Skopenkov2020e,  2, Sketch of a proof of (b1)].
If
2, Sketch of a proof of (b1)].
If  is pairwise unlinked, then the number
is pairwise unlinked, then the number 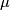 is independent of permutation of the components, up to multiplication by
is independent of permutation of the components, up to multiplication by 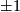 [HaefligerSteer1965] (this can be easily proved directly).
[HaefligerSteer1965] (this can be easily proved directly).
(f) The Borromean link is non-trivial also because joining the three components with two tubes (i.e. `linked analogue' of embedded connected sum of the components [Skopenkov2016c,  4]) yields a non-trivial knot [Haefliger1962, Theorem 4.3], cf. the Haefliger Trefoil knot [Skopenkov2016t, Example 2.1].
4]) yields a non-trivial knot [Haefliger1962, Theorem 4.3], cf. the Haefliger Trefoil knot [Skopenkov2016t, Example 2.1].
Next we present an example of the non-injectivity of the linking coefficient, which shows that the dimension restriction is sharp in Theorem 4.1.
Example 5.2 (Whitehead link). (a) For every positive integer  there is a non-trivial embedding
there is a non-trivial embedding 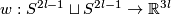 such that the second component is null-homotopic in the complement of the first component (i.e. the linking coefficient
such that the second component is null-homotopic in the complement of the first component (i.e. the linking coefficient 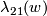 is trivial).
is trivial).
Such an embedding is obtained from the Borromean rings embedding by joining the second and the third components with a tube, i.e. by the `linked analogue' of the embedded connected sum of the components [Skopenkov2016c,  3,
3,  4]; see also the Wikipedia article on the Whitehead link. (For
4]; see also the Wikipedia article on the Whitehead link. (For 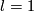 the connected sum is not well-defined, so we take the specific connected sum (w) from Figure 7.)
the connected sum is not well-defined, so we take the specific connected sum (w) from Figure 7.)
(b) The second component is null-homotopic in the complement of the first component by Example 5.1.b.
(c) For 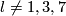 the Whitehead link is non-trivial because the first component is not null-homotopic in the complement of the second component.
More precisely,
the Whitehead link is non-trivial because the first component is not null-homotopic in the complement of the second component.
More precisely, 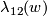 equals to the Whitehead square
equals to the Whitehead square ![[\iota_l,\iota_l]\ne0](/images/math/0/0/1/001153eef02a680fe884d6a411e57806.png) of the generator
of the generator 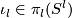 [Haefliger1962t, end of
[Haefliger1962t, end of  6] (I do not know a written proof of this except [Skopenkov2015a, the Whitehead link Lemma 2.14] for
6] (I do not know a written proof of this except [Skopenkov2015a, the Whitehead link Lemma 2.14] for  even).
For
even).
For 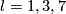 the Whitehead link is distinguished from the standard embedding by more complicated Sato-Levine invariant [Skopenkov2006a].
the Whitehead link is distinguished from the standard embedding by more complicated Sato-Levine invariant [Skopenkov2006a].
(d) This example (in higher dimensions, i.e. for  ) seems to have been discovered by Whitehead, in connection with Whitehead product.
) seems to have been discovered by Whitehead, in connection with Whitehead product.
(e) For some results on links 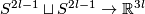 related to the Whitehead link see [Skopenkov2015a,
related to the Whitehead link see [Skopenkov2015a,  2.5].
2.5].
6 Linked manifolds
In this section we state some analogues of Theorem 4.2 where spheres are replaced by general manifolds. We start with a simple case where no high-connectivity assumptions are made on the source manifolds.
Theorem 6.1. Assume that 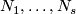 are closed connected manifolds and
are closed connected manifolds and  for every
for every  . Then for an embedding
. Then for an embedding 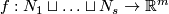 and every
and every 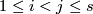 one defines the linking coefficient
one defines the linking coefficient 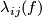 , see Remark 3.2.e. We have
, see Remark 3.2.e. We have 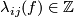 if both
if both 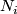 and
and 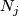 are orientable, and
are orientable, and 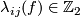 otherwise. Then the collection of pairwise linking coefficients
otherwise. Then the collection of pairwise linking coefficients
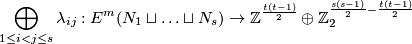
is well-defined and is a 1-1 correspondence, where  of
of 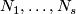 are orientable and
are orientable and 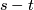 are not.
are not.
We present the general case of the classification of embeddings of disjoint highly-connected manifolds only for the case of two oriented components of the same dimension.
Theorem 6.2. Let 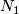 and
and 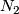 be closed
be closed  -dimensional homologically
-dimensional homologically 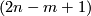 -connected orientable manifolds. For an embedding
-connected orientable manifolds. For an embedding 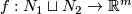 one can define the invariant
one can define the invariant 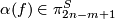 analogously to Definition 3.3. Then
analogously to Definition 3.3. Then
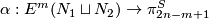
is well-defined and is a 1-1 correspondence, provided 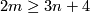 .
.
Theorems 6.1 and 6.2 are easily deduced from the Zeeman/Haefliger Unknotting Theorem in the PL/smooth category [Ivansic&Horvatic1974]. They are also corollaries of [Skopenkov2006, the Haefliger-Weber Theorem 5.4] (in both categories); the calculations are analogous to the construction of the 1-1 correspondence ![[S^p\times S^q,S^{m-1}]\to\pi^S_{p+q+1-m}](/images/math/2/b/0/2b09988667478f4877c99836023893d9.png) in Definition 3.3.
See [Skopenkov2000, Proposition 1.2] for the link map analogue.
in Definition 3.3.
See [Skopenkov2000, Proposition 1.2] for the link map analogue.
Now we present an extension of Theorems 6.1 and 6.2 to a case where 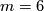 and
and 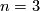 . In particular, for the results below
. In particular, for the results below 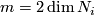 ,
, 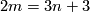 and the manifolds
and the manifolds 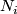 are only
are only  -connected. An embedding
-connected. An embedding 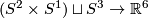 is Brunnian if its restriction to each component is isotopic to the standard embedding. For each triple of integers
is Brunnian if its restriction to each component is isotopic to the standard embedding. For each triple of integers 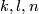 such that
such that 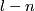 is even, Avvakumov has constructed a Brunnian embedding
is even, Avvakumov has constructed a Brunnian embedding 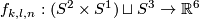 , which appears in the next result [Avvakumov2016,
, which appears in the next result [Avvakumov2016,  1].
1].
Theorem 6.3. [Avvakumov2016, Theorem 1]
Any Brunnian embedding 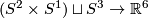 is isotopic to
is isotopic to 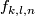 for some integers
for some integers 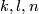 such that
such that 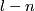 is even. Two embeddings
is even. Two embeddings 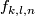 and
and 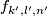 are isotopic if and only if
are isotopic if and only if 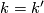 and both
and both 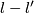 and
and 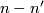 are divisible by
are divisible by 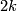 .
.
The proof uses M. Skopenkov's classification of embeddings 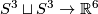 (Theorem 8.1 for
(Theorem 8.1 for 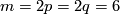 ). The following corollary shows that the relation between the embeddings
). The following corollary shows that the relation between the embeddings 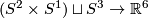 and
and 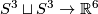 is not trivial.
is not trivial.
Corollary 6.4. [Avvakumov2016, Corollary 1], cf. [Skopenkov2016t, Corollary 3.5.b]
There exist embeddings 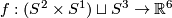 and
and 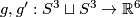 such that the componentwise embedded connected sum
such that the componentwise embedded connected sum 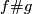 is isotopic to
is isotopic to 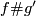 but
but  is not isotopic to
is not isotopic to 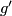 .
.
For an unpublished generalization of Theorem 6.3 and Corollary 6.4 see [Avvakumov2017].
7 Reduction to the case with unknotted components
In this section we assume that 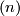 is an
is an  -tuple such that
-tuple such that 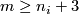 .
.
Define 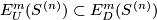 to be the subgroup of links all whose components are unknotted, i.e. isotopic to the standard embedding
to be the subgroup of links all whose components are unknotted, i.e. isotopic to the standard embedding 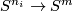 . We remark that
. We remark that 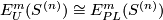 [Haefliger1966a,
[Haefliger1966a,  2.4, 2.6 and 9.3], [Crowley&Ferry&Skopenkov2011,
2.4, 2.6 and 9.3], [Crowley&Ferry&Skopenkov2011,  1.5].
1.5].
Define the restriction homomorphism by mapping the isotopy class of a link to the ordered  -tuple of the isotopy classes of its components:
-tuple of the isotopy classes of its components:
![\displaystyle r \colon E^m_D(S^{(n)}) \to \bigoplus_{i=1}^s E^m_D(S^{n_i}), \quad r[f]:=\oplus_{i=1}^s [f|_{S^{n_i}} \colon S^{n_i} \to S^m].](/images/math/2/5/d/25d2ec311c8371fe4ac42f34989c9ad0.png)
Take  pairwise disjoint
pairwise disjoint  -discs in
-discs in 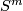 , i.e. take an embedding
, i.e. take an embedding  . Define
. Define
![\displaystyle j \colon \bigoplus_{i=1}^s E^m_D(S^{n_i}) \to E^m_D(S^{(n)})\quad\text{by}\quad j([f_1], \ldots, [f_s]):=[(g\circ\sqcup_{i=1}^s f_i):S^{(n)}\to S^m].](/images/math/3/2/9/329c5a3b46fae2defd6d32e45fb15014.png)
Then  is a right inverse of the restriction homomorphism
is a right inverse of the restriction homomorphism  , i.e.
, i.e. 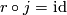 .
The unknotting homomorphism
.
The unknotting homomorphism  is defined to be the homomorphism
is defined to be the homomorphism
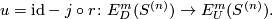
Informally, the homomorphism  is obtained by taking embedded connected sums of components with knots
is obtained by taking embedded connected sums of components with knots 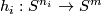 representing the elements of
representing the elements of 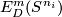 inverse to the components, whose images
inverse to the components, whose images 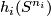 are small and are close to the components.
are small and are close to the components.
For some information on the groups 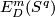 see [Skopenkov2016s], [Skopenkov2006,
see [Skopenkov2016s], [Skopenkov2006,  3.3].
3.3].
8 Classification beyond the metastable range
Theorem 8.1.
[Haefliger1966a, Theorem 10.7], [Skopenkov2009, Theorem 1.1], [Skopenkov2006b, Theorem 1.1]
If 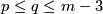 and
and 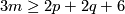 , then there is a homomorphism
, then there is a homomorphism 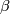 for which the following map is an isomorphism
for which the following map is an isomorphism
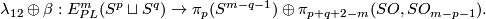
The map 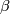 and its right inverse
and its right inverse 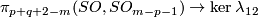 are constructed in [Haefliger1966a,
are constructed in [Haefliger1966a,  10] and in [Haefliger1966, 8.13], respectively. For alternative geometric (and presumably equivalent) definitions of
10] and in [Haefliger1966, 8.13], respectively. For alternative geometric (and presumably equivalent) definitions of 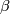 see [Skopenkov2009,
see [Skopenkov2009,  3], [Skopenkov2006b,
3], [Skopenkov2006b,  5], cf. [Skopenkov2007,
5], cf. [Skopenkov2007,  2] and [Crowley&Skopenkov2016,
2] and [Crowley&Skopenkov2016,  2.3]. For a historical remark see [Skopenkov2009, the second paragraph in p. 2].
2.3]. For a historical remark see [Skopenkov2009, the second paragraph in p. 2].
Remark 8.2.
(a) Theorem 8.1 implies that for any 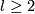 we have an isomorphism
we have an isomorphism
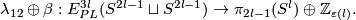
(b) For any 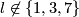 , the map
, the map
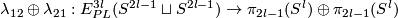
is injective and its image is 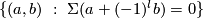 .
.
For 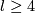 see [Haefliger1962t,
see [Haefliger1962t,  6]. The following proof for
6]. The following proof for 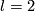 and general remark are intended for specialists.
and general remark are intended for specialists.
For 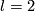 there is an exact sequence
there is an exact sequence 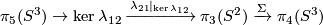 ,
where
,
where 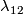 is
is 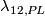 [Haefliger1966a, Corollary 10.3].
We have
[Haefliger1966a, Corollary 10.3].
We have 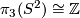 ,
, 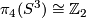 and
and  is the reduction modulo 2.
By the exactness of the previous sequence,
is the reduction modulo 2.
By the exactness of the previous sequence, 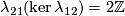 .
By (a)
.
By (a) 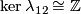 .
Hence
.
Hence  is injective.
We have
is injective.
We have 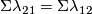 by [Haefliger1966a, Proposition 10.2].
So the formula of (b) follows.
by [Haefliger1966a, Proposition 10.2].
So the formula of (b) follows.
Analogously to [Skopenkov2009, Theorem 3.5] using geometric definitons of 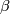 [Skopenkov2009,
[Skopenkov2009,  3], [Skopenkov2006b,
3], [Skopenkov2006b,  5] and geomeric interpretation of the EHP sequence
5] and geomeric interpretation of the EHP sequence 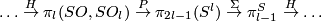 [Koschorke&Sanderson1977, Main Theorem in
[Koschorke&Sanderson1977, Main Theorem in  1] one can possibly prove that
1] one can possibly prove that 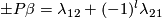 . Then (b) would follow.
. Then (b) would follow.
(c) For any 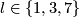 the map
the map 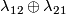 in (b) above is not injective [Haefliger1962t,
in (b) above is not injective [Haefliger1962t,  6].
6].
Theorem 8.3.
For any 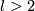 there an isomorphism
there an isomorphism
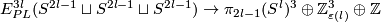
which is the sum of 3 pairwise invariants of Remark 8.2.a, and the triple linking number ( 5).
5).
This follows from [Haefliger1966a, Theorem 9.4], see also [Haefliger1962t,  6].
6].
9 Classification in codimension at least 3
In this section we assume that 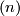 is an
is an  -tuple such that
-tuple such that 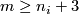 .
For this case a readily calculable classification of
.
For this case a readily calculable classification of 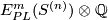 was obtained in
[Crowley&Ferry&Skopenkov2011, Theorem 1.9]. In particular, [Crowley&Ferry&Skopenkov2011,
was obtained in
[Crowley&Ferry&Skopenkov2011, Theorem 1.9]. In particular, [Crowley&Ferry&Skopenkov2011,  1.2] contains necessary and sufficient conditions on
1.2] contains necessary and sufficient conditions on 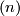 which determine when
which determine when 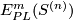 is finite. These results are elementary, but the precise formulations are technical. Hence, we only state the following corollary of [Crowley&Ferry&Skopenkov2011, Theorem 1.9 and
is finite. These results are elementary, but the precise formulations are technical. Hence, we only state the following corollary of [Crowley&Ferry&Skopenkov2011, Theorem 1.9 and  1.2] and describe the methods of its proof in Definition 9.2 and Theorem 9.3 below.
1.2] and describe the methods of its proof in Definition 9.2 and Theorem 9.3 below.
Theorem 9.1. There are algorithms which for integers 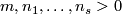
Tex syntax error.
(b) determine whether 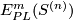 is finite.
is finite.
Definition 9.2 (The Haefliger link sequence). In [Haefliger1966a, 1.2-1.5] Haefliger defined a long exact sequence of abelian groups
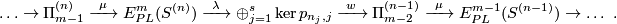
We briefly define the groups and homomorphisms in this sequence, refering to [Haefliger1966a, 1.4] for details.
We first note that in the sequence above the  -tuples
-tuples 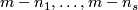 are the same for different terms.
Denote
are the same for different terms.
Denote 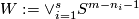 .
For any
.
For any 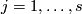 and positive integer
and positive integer  denote by
denote by 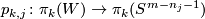 the homomorphism induced by the collapse map onto to the
the homomorphism induced by the collapse map onto to the  -component of the wedge. Denote
-component of the wedge. Denote 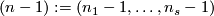 and
and 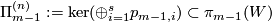 .
.
It can be shown that each component of a link 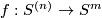 has a non-zero normal vector field. So each component of a link can be pushed off along such a vector field into the complement
has a non-zero normal vector field. So each component of a link can be pushed off along such a vector field into the complement 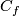 . Analogously to Definition 3.1 there is a canonical homotopy equivalence
. Analogously to Definition 3.1 there is a canonical homotopy equivalence 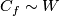 . It can also be shown that the homotopy class in
. It can also be shown that the homotopy class in 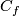 of the push off of the
of the push off of the  th component gives a well-defined map
th component gives a well-defined map 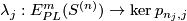 . In fact, the map
. In fact, the map 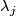 is a generalization of the linking coefficient. Finally, define
is a generalization of the linking coefficient. Finally, define 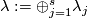 .
.
Taking the Whitehead product with the class of the inclusion of 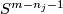 into
into  defines a homomorphism
defines a homomorphism 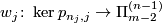 . Define
. Define 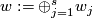 .
.
The definition of the homomorphism 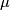 is given in [Haefliger1966a, 1.5].
is given in [Haefliger1966a, 1.5].
Theorem 9.3. (a) [Haefliger1966a, Theorem 1.3] The Haefliger link sequence is exact.
(b) The map 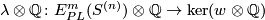 is an isomorphism.
is an isomorphism.
Part (b) follows because 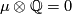 [Crowley&Ferry&Skopenkov2011, Lemma 1.3], and so the Haefliger link sequence after tensoring with the rational numbers
[Crowley&Ferry&Skopenkov2011, Lemma 1.3], and so the Haefliger link sequence after tensoring with the rational numbers 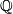 splits into short exact sequences.
splits into short exact sequences.
In general, the computation of the groups and homomorphisms appearing in Theorem 9.3 is difficult. For (a) no computations are known except for those giving (b) and those giving Theorem 8.1 for 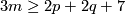 (note that Theorem 8.1 has a direct proof easier than proof of Theorem 9.3.a). For (b) the computations constitute most of [Crowley&Ferry&Skopenkov2011]. Hence Theorem 9.3 is not a readily calculable classification in general.
(note that Theorem 8.1 has a direct proof easier than proof of Theorem 9.3.a). For (b) the computations constitute most of [Crowley&Ferry&Skopenkov2011]. Hence Theorem 9.3 is not a readily calculable classification in general.
10 References
- [Avvakumov2016] S. Avvakumov, The classification of certain linked 3-manifolds in 6-space, Moscow Mathematical Journal, 16:1 (2016) 1-25. http://arxiv.org/abs/1408.3918.
- [Avvakumov2017] S. Avvakumov, The classification of linked 3-manifolds in 6-space, Algebraic & Geometric Topology, to appear. arxiv preprint.
- [Crowley&Ferry&Skopenkov2011] D. Crowley, S.C. Ferry, M. Skopenkov, The rational classification of links of codimension >2, Forum Math. 26 (2014), 239-269. https://arxiv.org/abs/1106.1455
- [Crowley&Skopenkov2016] D. Crowley and A. Skopenkov, Embeddings of non-simply-connected 4-manifolds in 7-space, I. Classification modulo knots, Moscow Math. J., 21 (2021), 43--98. arXiv:1611.04738.
- [Haefliger1962] A. Haefliger, Knotted
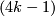 -spheres in
-spheres in 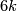 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [HaefligerSteer1965] A. Haefliger and B. Steer, Symmetry of linking coefficients, Comment. Math. Helv., 39 (1965), 259--270.pdf
- [Ivansic&Horvatic1974] I. Ivan\v{s}i\'c and K. Horvati\'c, On unlinking of polyhedra, Glasnik Mat. 9(29) (1974) 147-153.
- [Kervaire1959a] M. Kervaire, An interpretation of G. Whitehead's generalization of H. Hopf's invariant, Ann. of Math. 62 (1959) 345--362.
- [Koschorke&Sanderson1977] U. Koschorke and B. Sanderson, Geometric interpretation of the generalized Hopf invariant, Math. Scand. 41 (1977) 199--217.
- [Koschorke1988] U. Koschorke, Link maps and the geometry of their invariants, Manuscripta Math. 61:4 (1988) 383--415.
- [Massey1968] W. S. Massey, Higher order linking numbers, Proc. Conf. on Algebraic Topology, Univ. Illinois, Chicago Circle, Chicago, Ill., (1968) pp. 174--205. MR0254832 (40 #8039), see also MR1625365 (99e:57016) massey.pdf.
- [Massey1990] W. S. Massey, Homotopy classification of 3-component links of codimension greater than 2, Topol. Appl. 34 (1990) 269--300.
- [Skopenkov2000] A. Skopenkov, On the generalized Massey-Rolfsen invariant for link maps, Fund. Math. 165 (2000), 1-15.
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2006a] A. Skopenkov, Classification of embeddings below the metastable dimension. Available at the arXiv:0607422.
- [Skopenkov2006b] M. Skopenkov, A formula for the group of links in the 2-metastable dimension, arxiv:math/0610320v1
- [Skopenkov2007] A. Skopenkov, A new invariant and parametric connected sum of embeddings, Fund. Math. 197 (2007), 253–269. arXiv:math/0509621. MR2365891 (2008k:57044) Zbl 1145.57019
- [Skopenkov2009] M. Skopenkov, Suspension theorems for links and link maps. Proc. AMS 137 (2009) 359--369. arxiv:math/0610320, version 2 or higher
- [Skopenkov2015] M. Skopenkov, When is the set of embeddings finite up to isotopy? Intern. J. Math. 26:7 (2015), http://arxiv.org/abs/1106.1878
- [Skopenkov2015a] A. Skopenkov, A classification of knotted tori, Proc. A of the Royal Society of Edinburgh, 150:2 (2020), 549-567. Full version: http://arxiv.org/abs/1502.04470
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016e] A. Skopenkov, Embeddings just below the stable range: classification, to appear in Bull. Man. Atl.
- [Skopenkov2016i] A. Skopenkov, Isotopy, submitted to Bull. Man. Atl.
- [Skopenkov2016k] A. Skopenkov, Knotted tori, preprint.
- [Skopenkov2016s] A. Skopenkov, Knots, i.e. embeddings of spheres, preprint.
- [Skopenkov2016t] A. Skopenkov, 3-manifolds in 6-space, to appear in Boll. Man. Atl.
- [Skopenkov2020e] A. Skopenkov, Extendability of simplicial maps is undecidable, Discr. Comp. Geom., 69:1 (2023), 250–259. arXiv:2008.00492
- [Zeeman1962] E. C. Zeeman, Isotopies and knots in manifolds, Topology of 3-manifolds and related topics (Proc. The Univ. of Georgia Institute, 1961), Prentice-Hall (1962), 187–193. MR0140097 (25 #3520) Zbl 1246.57069
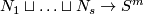 , where
, where 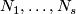 are spheres (or even closed manifolds) and
are spheres (or even closed manifolds) and 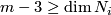 for every
for every  , under some further restrictions. For a related classification of knotted tori see [Skopenkov2016k].
, under some further restrictions. For a related classification of knotted tori see [Skopenkov2016k].
For an  -tuple
-tuple 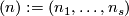 denote
denote 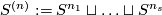 . Although
. Although 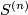 is not a manifold when
is not a manifold when 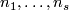 are not all equal, embeddings
are not all equal, embeddings 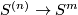 and isotopy between such embeddings are defined analogously to the case of manifolds [Skopenkov2016i]. Denote by
and isotopy between such embeddings are defined analogously to the case of manifolds [Skopenkov2016i]. Denote by 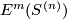 the set of embeddings
the set of embeddings 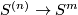 up to isotopy.
up to isotopy.
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3].
3].
The following table was obtained by Zeeman around 1960 (see the Haefliger-Zeeman Theorem 4.1 below):
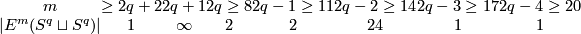
A component-wise version of embedded connected sum [Skopenkov2016c,  5] defines a commutative group structure on the set
5] defines a commutative group structure on the set 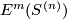 for
for 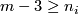 [Haefliger1966a, 2.5], [Skopenkov2015, Group Structure Lemma 2.2 and Remark 2.3.a], [Avvakumov2016,
[Haefliger1966a, 2.5], [Skopenkov2015, Group Structure Lemma 2.2 and Remark 2.3.a], [Avvakumov2016,  1], [Avvakumov2017,
1], [Avvakumov2017,  1.4], see Figure 1.
1.4], see Figure 1.
The standard embedding 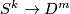 is defined by
is defined by 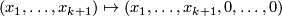 . Fix
. Fix  pairwise disjoint
pairwise disjoint  -discs
-discs 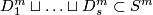 . The standard embedding
. The standard embedding 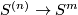 is defined by taking the union of the compositions of the standard embeddings
is defined by taking the union of the compositions of the standard embeddings 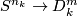 with the fixed inclusions
with the fixed inclusions 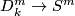 .
.
2 Examples
Recall that for any  -manifold
-manifold  and
and 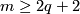 , every two embeddings
, every two embeddings 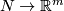 are isotopic [Skopenkov2016c, General Position Theorem 2.1], [Skopenkov2006, General Position Theorem 2.1].
The following example shows that the restriction
are isotopic [Skopenkov2016c, General Position Theorem 2.1], [Skopenkov2006, General Position Theorem 2.1].
The following example shows that the restriction 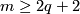 is sharp for non-connected manifolds.
is sharp for non-connected manifolds.
Example 2.1 (The Hopf Link).
(a) For every positive integer  there is an embedding
there is an embedding 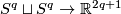 , which is not isotopic to the standard embedding.
, which is not isotopic to the standard embedding.
For 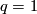 the Hopf link is shown in Figure 2. For all
the Hopf link is shown in Figure 2. For all  the image of the Hopf link is the union of two
the image of the Hopf link is the union of two  -spheres which can be described as follows:
-spheres which can be described as follows:
- either the spheres are
 and
and  in
in 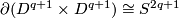 ;
;
- or they are given as the sets of points in
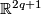 satisfying the following equations:
satisfying the following equations:
This embedding is distinguished from the standard embedding by the linking number (cf.  3).
3).
(b) For any 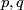 there is an embedding
there is an embedding 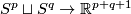 which is not isotopic to the standard embedding.
which is not isotopic to the standard embedding.
Analogously to (a), the image is the union of two spheres which can be described as follows:
- either the spheres are
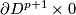 and
and 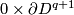 in
in 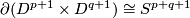 .
.
- or they are given as the points in
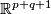 satisfying the following equations:
satisfying the following equations:
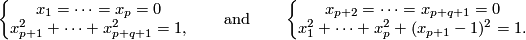
This embedding is also distinguished from the standard embedding by the linking number (cf.  3).
3).
Definition 2.2 (A link with prescribed linking coefficient). We define the `Zeeman' map
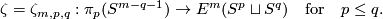
For a map 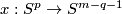 representing an element of
representing an element of 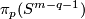 let
let
Tex syntax error
Tex syntax error. Let
Tex syntax error.
One can easily check that  is well-defined and is a homomorphism.
is well-defined and is a homomorphism.
3 The linking coefficient
Here we define the linking coefficient and discuss its properties. Fix orientations of the standard spheres and balls.
Definition 3.1 (The linking coefficient). We define a map
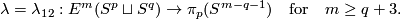
Take an embedding 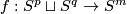 representing an element
representing an element ![[f]\in E^m(S^p\sqcup S^q)](/images/math/9/5/8/958e4adb33de7e2445e035db1cbd05a0.png) .
Take an embedding
.
Take an embedding 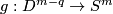 such that
such that 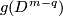 intersects
intersects 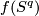 transversely at exactly one point with positive sign; see Figure 4.
transversely at exactly one point with positive sign; see Figure 4.
Then the restriction 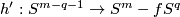 of
of  to
to 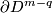 is a homotopy equivalence.
is a homotopy equivalence.
(Indeed, since 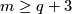 , by general position the complement
, by general position the complement 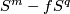 is simply-connected.
By Alexander duality,
is simply-connected.
By Alexander duality, 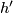 induces isomorphism in homology.
Hence by the Hurewicz and Whitehead theorems
induces isomorphism in homology.
Hence by the Hurewicz and Whitehead theorems 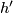 is a homotopy equivalence.)
is a homotopy equivalence.)
Let  be a homotopy inverse of
be a homotopy inverse of 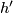 .
Define
.
Define
![\displaystyle \lambda[f]=\lambda_{12}[f]:=[S^p\xrightarrow{~f|_{S^p}~} S^m-fS^q\overset h\to S^{m-q-1}]\in\pi_p(S^{m-q-1}).](/images/math/7/0/2/702421c61c119e9f17cfea8b085f374a.png)
Remark 3.2.
(a) Clearly, ![\lambda[f]](/images/math/4/6/0/4603ad5fae840a15ed28fd021825efae.png) is well-defined, i.e. is independent of the choices of
is well-defined, i.e. is independent of the choices of 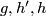 and of the representative
and of the representative  of
of ![[f]](/images/math/d/d/4/dd43b82529dd8d403c1585c5d151a163.png) .
One can check that
.
One can check that  is a homomorphism.
is a homomorphism.
(b) Analogously one can define ![\lambda_{21}[f]\in\pi_q(S^{m-p-1})](/images/math/5/b/8/5b81499fd01f4267c2347d2439817f40.png) for
for 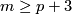 , by exchanging
, by exchanging  and
and  in the above definition.
in the above definition.
(c) Clearly, 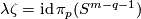 for the Zeeman map
for the Zeeman map 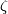 . So
. So  is surjective and
is surjective and 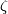 is injective.
is injective.
(d) For 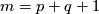 there is a simpler alternative definition using homological ideas. That definition can be generalized to the case where the components are closed orientable manifolds. Cf. Remark 5.3.f of [Skopenkov2016e].
there is a simpler alternative definition using homological ideas. That definition can be generalized to the case where the components are closed orientable manifolds. Cf. Remark 5.3.f of [Skopenkov2016e].
Recall that by the Freudenthal Suspension Theorem the stable suspension homomorphism 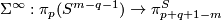 is an isomorphism for
is an isomorphism for 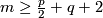 . The stable suspension of the linking coefficient can be described as follows.
. The stable suspension of the linking coefficient can be described as follows.
Definition 3.3 (The  -invariant). We define a map
-invariant). We define a map
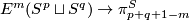 for
for 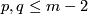 .
Take an embedding
.
Take an embedding 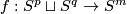 representing an element
representing an element ![[f]\in E^m(S^p\sqcup S^q)](/images/math/9/5/8/958e4adb33de7e2445e035db1cbd05a0.png) .
Define the Gauss map (see Figure 4)
.
Define the Gauss map (see Figure 4)
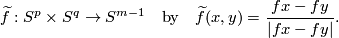
For 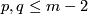 define the
define the  -invariant by
-invariant by
![\displaystyle \alpha[f]=[\widetilde f]\in[S^p\times S^q,S^{m-1}]\overset{v^*}\cong\pi_{p+q}(S^{m-1})\cong\pi^S_{p+q+1-m}.](/images/math/5/3/d/53debfbd4a5d88f0c6d79b4fce1d64a3.png)
The second isomorphism in this formula is the suspension isomorphism.
The map 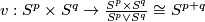 is the quotient map, see Figure 5.
is the quotient map, see Figure 5.
The map 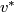 is a 1--1 correspondence for
is a 1--1 correspondence for 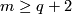 .
(For
.
(For 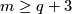 this follows by general position and for
this follows by general position and for 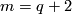 by the cofibration Barratt-Puppe exact sequence of pair
by the cofibration Barratt-Puppe exact sequence of pair 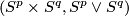 and by the existence of a retraction
and by the existence of a retraction 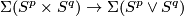 .)
.)
One can easily check that  is well-defined and for
is well-defined and for 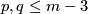 is a homomorphism.
is a homomorphism.
Lemma 3.4 [Kervaire1959a, Lemma 5.1].
We have 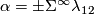 for
for 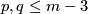 .
.
Hence 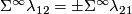 , even though in general
, even though in general 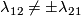 as we explain in Example 5.2.a,c.
as we explain in Example 5.2.a,c.
Note that the  -invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006,
-invariant can be defined in more general situations [Koschorke1988], [Skopenkov2006,  5].
5].
4 Classification in the metastable range
The Haefliger-Zeeman Theorem 4.1.
If 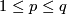 , then both
, then both  and
and 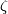 are isomorphisms for
are isomorphisms for 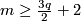 in the smooth category, and for
in the smooth category, and for 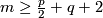 in the PL category.
in the PL category.
The surjectivity of  (or the injectivity of
(or the injectivity of  ) follows from
) follows from 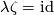 .
The injectivity of
.
The injectivity of  (or the surjectivity of
(or the surjectivity of 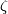 ) is proved in [Haefliger1962t, Theorem in
) is proved in [Haefliger1962t, Theorem in  5], [Zeeman1962]
(or follows from [Skopenkov2006, the Haefliger-Weber Theorem 5.4 and the Deleted Product Lemma 5.3.a]).
5], [Zeeman1962]
(or follows from [Skopenkov2006, the Haefliger-Weber Theorem 5.4 and the Deleted Product Lemma 5.3.a]).
An analogue of this result holds for links with many components, each of the same dimension [Haefliger1962t, Theorem in  5]. Let
5]. Let 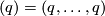 be the
be the  -tuple consisting entirely of some positive integer
-tuple consisting entirely of some positive integer  .
.
Theorem 4.2. The collection of pairwise linking coefficients
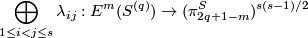
is a 1-1 correspondence for 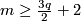 .
.
5 Examples beyond the metastable range
For 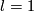 the results of this section are parts of low-dimensional link theory, so they were known well before given references.
the results of this section are parts of low-dimensional link theory, so they were known well before given references.
First we present an example of the non-injectivity of the collection of pairwise linking coefficients, which shows that the dimension restriction is sharp in Theorem 4.2.
Example 5.1 (Borromean rings).
(a) There is a non-trivial embedding 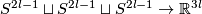 whose restriction to each 2-component sublink is trivial [Haefliger1962, 4.1], [Haefliger1962t,
whose restriction to each 2-component sublink is trivial [Haefliger1962, 4.1], [Haefliger1962t,  6].
6].
In order to construct such an embedding, denote coordinates in 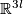 by
by 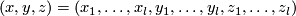 .
The (higher-dimensional) `Borromean spheres' are given by the following three systems of equations:
.
The (higher-dimensional) `Borromean spheres' are given by the following three systems of equations:
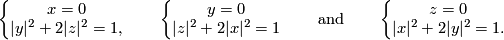
See Figure 6. The required embedding, called Borromean link, is any embedding whose image is the union of the Borromean spheres.
(b) By moving two of the Borromean spheres and self-intersecting them, we can drag the remaining sphere far away from the two.
More precisely, each two of the Borromean spheres span two (intersecting) 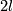 -disks disjoint from the remaining sphere.
-disks disjoint from the remaining sphere.
(c) Restriction of the Borromean link to each 2-component sublink is trivial, because each two of the Borromean spheres span two disjoint  -disks (intersecting the remaining sphere).
Moreover, we can take these
-disks (intersecting the remaining sphere).
Moreover, we can take these 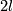 -disks so that
-disks so that
- each one of them intersects the remaining sphere transversely by an
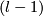 -sphere;
-sphere;
- the obtained two disjoint
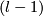 -spheres in the remaining sphere have linking number
-spheres in the remaining sphere have linking number 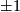 , i.e. one of them spans an
, i.e. one of them spans an  -disk (in the remaining sphere) itersecting the other transversely at exacly one point.
-disk (in the remaining sphere) itersecting the other transversely at exacly one point.
(d) The Borromean link is distinguished from the standard embedding by triple linking number of Milnor-Haefliger-Steer-Massey defined as follows (cf. (c)).
Take a 3-component link, i.e. an embedding 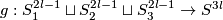 .
Assume that
.
Assume that  is pairwise unlinked, i.e. every two components are contained in disjoint smooth balls.
Let
is pairwise unlinked, i.e. every two components are contained in disjoint smooth balls.
Let 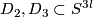 be disjoint oriented embedded
be disjoint oriented embedded 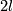 -disks in general position to
-disks in general position to  , and such that
, and such that 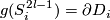 for
for 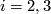 .
Then for
.
Then for 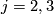 the preimage
the preimage 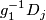 is an oriented
is an oriented 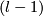 -submanifold of
-submanifold of 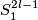 missing
missing 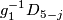 .
Let
.
Let 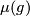 be the linking number of
be the linking number of 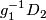 and
and 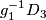 in
in 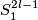 .
.
(e) In a standard way one checks that the triple linking number is well-defined, i.e. is independent of the choice of 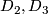 , and of the isotopy of
, and of the isotopy of  .
The above definition is equivalent to the standard definition of Milnor-Haefliger-Steer-Massey number [Haefliger1962t,
.
The above definition is equivalent to the standard definition of Milnor-Haefliger-Steer-Massey number [Haefliger1962t,  4], [HaefligerSteer1965], [Haefliger1966a, proof of Theorem 9.4], [Massey1968], [Massey1990,
4], [HaefligerSteer1965], [Haefliger1966a, proof of Theorem 9.4], [Massey1968], [Massey1990,  7] by the well-known `linking number' definition of the Whitehead invariant
7] by the well-known `linking number' definition of the Whitehead invariant 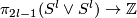 [Skopenkov2020e,
[Skopenkov2020e,  2, Sketch of a proof of (b1)].
If
2, Sketch of a proof of (b1)].
If  is pairwise unlinked, then the number
is pairwise unlinked, then the number  is independent of permutation of the components, up to multiplication by
is independent of permutation of the components, up to multiplication by  [HaefligerSteer1965] (this can be easily proved directly).
[HaefligerSteer1965] (this can be easily proved directly).
(f) The Borromean link is non-trivial also because joining the three components with two tubes (i.e. `linked analogue' of embedded connected sum of the components [Skopenkov2016c,  4]) yields a non-trivial knot [Haefliger1962, Theorem 4.3], cf. the Haefliger Trefoil knot [Skopenkov2016t, Example 2.1].
4]) yields a non-trivial knot [Haefliger1962, Theorem 4.3], cf. the Haefliger Trefoil knot [Skopenkov2016t, Example 2.1].
Next we present an example of the non-injectivity of the linking coefficient, which shows that the dimension restriction is sharp in Theorem 4.1.
Example 5.2 (Whitehead link). (a) For every positive integer  there is a non-trivial embedding
there is a non-trivial embedding 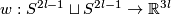 such that the second component is null-homotopic in the complement of the first component (i.e. the linking coefficient
such that the second component is null-homotopic in the complement of the first component (i.e. the linking coefficient 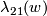 is trivial).
is trivial).
Such an embedding is obtained from the Borromean rings embedding by joining the second and the third components with a tube, i.e. by the `linked analogue' of the embedded connected sum of the components [Skopenkov2016c,  3,
3,  4]; see also the Wikipedia article on the Whitehead link. (For
4]; see also the Wikipedia article on the Whitehead link. (For 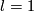 the connected sum is not well-defined, so we take the specific connected sum (w) from Figure 7.)
the connected sum is not well-defined, so we take the specific connected sum (w) from Figure 7.)
(b) The second component is null-homotopic in the complement of the first component by Example 5.1.b.
(c) For 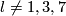 the Whitehead link is non-trivial because the first component is not null-homotopic in the complement of the second component.
More precisely,
the Whitehead link is non-trivial because the first component is not null-homotopic in the complement of the second component.
More precisely, 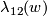 equals to the Whitehead square
equals to the Whitehead square ![[\iota_l,\iota_l]\ne0](/images/math/0/0/1/001153eef02a680fe884d6a411e57806.png) of the generator
of the generator 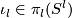 [Haefliger1962t, end of
[Haefliger1962t, end of  6] (I do not know a written proof of this except [Skopenkov2015a, the Whitehead link Lemma 2.14] for
6] (I do not know a written proof of this except [Skopenkov2015a, the Whitehead link Lemma 2.14] for  even).
For
even).
For  the Whitehead link is distinguished from the standard embedding by more complicated Sato-Levine invariant [Skopenkov2006a].
the Whitehead link is distinguished from the standard embedding by more complicated Sato-Levine invariant [Skopenkov2006a].
(d) This example (in higher dimensions, i.e. for  ) seems to have been discovered by Whitehead, in connection with Whitehead product.
) seems to have been discovered by Whitehead, in connection with Whitehead product.
(e) For some results on links  related to the Whitehead link see [Skopenkov2015a,
related to the Whitehead link see [Skopenkov2015a,  2.5].
2.5].
6 Linked manifolds
In this section we state some analogues of Theorem 4.2 where spheres are replaced by general manifolds. We start with a simple case where no high-connectivity assumptions are made on the source manifolds.
Theorem 6.1. Assume that 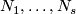 are closed connected manifolds and
are closed connected manifolds and  for every
for every  . Then for an embedding
. Then for an embedding 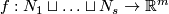 and every
and every 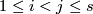 one defines the linking coefficient
one defines the linking coefficient 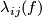 , see Remark 3.2.e. We have
, see Remark 3.2.e. We have 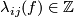 if both
if both 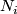 and
and 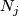 are orientable, and
are orientable, and 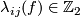 otherwise. Then the collection of pairwise linking coefficients
otherwise. Then the collection of pairwise linking coefficients
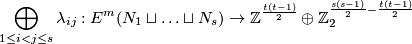
is well-defined and is a 1-1 correspondence, where  of
of 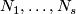 are orientable and
are orientable and 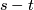 are not.
are not.
We present the general case of the classification of embeddings of disjoint highly-connected manifolds only for the case of two oriented components of the same dimension.
Theorem 6.2. Let 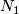 and
and 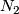 be closed
be closed  -dimensional homologically
-dimensional homologically 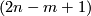 -connected orientable manifolds. For an embedding
-connected orientable manifolds. For an embedding 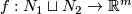 one can define the invariant
one can define the invariant 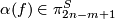 analogously to Definition 3.3. Then
analogously to Definition 3.3. Then
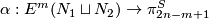
is well-defined and is a 1-1 correspondence, provided 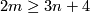 .
.
Theorems 6.1 and 6.2 are easily deduced from the Zeeman/Haefliger Unknotting Theorem in the PL/smooth category [Ivansic&Horvatic1974]. They are also corollaries of [Skopenkov2006, the Haefliger-Weber Theorem 5.4] (in both categories); the calculations are analogous to the construction of the 1-1 correspondence ![[S^p\times S^q,S^{m-1}]\to\pi^S_{p+q+1-m}](/images/math/2/b/0/2b09988667478f4877c99836023893d9.png) in Definition 3.3.
See [Skopenkov2000, Proposition 1.2] for the link map analogue.
in Definition 3.3.
See [Skopenkov2000, Proposition 1.2] for the link map analogue.
Now we present an extension of Theorems 6.1 and 6.2 to a case where 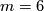 and
and 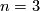 . In particular, for the results below
. In particular, for the results below 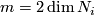 ,
, 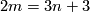 and the manifolds
and the manifolds 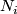 are only
are only  -connected. An embedding
-connected. An embedding 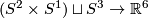 is Brunnian if its restriction to each component is isotopic to the standard embedding. For each triple of integers
is Brunnian if its restriction to each component is isotopic to the standard embedding. For each triple of integers 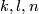 such that
such that 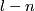 is even, Avvakumov has constructed a Brunnian embedding
is even, Avvakumov has constructed a Brunnian embedding 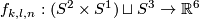 , which appears in the next result [Avvakumov2016,
, which appears in the next result [Avvakumov2016,  1].
1].
Theorem 6.3. [Avvakumov2016, Theorem 1]
Any Brunnian embedding 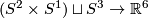 is isotopic to
is isotopic to 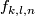 for some integers
for some integers 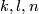 such that
such that 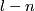 is even. Two embeddings
is even. Two embeddings 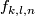 and
and 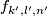 are isotopic if and only if
are isotopic if and only if 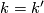 and both
and both 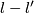 and
and 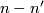 are divisible by
are divisible by 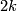 .
.
The proof uses M. Skopenkov's classification of embeddings 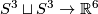 (Theorem 8.1 for
(Theorem 8.1 for 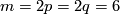 ). The following corollary shows that the relation between the embeddings
). The following corollary shows that the relation between the embeddings 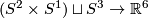 and
and 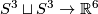 is not trivial.
is not trivial.
Corollary 6.4. [Avvakumov2016, Corollary 1], cf. [Skopenkov2016t, Corollary 3.5.b]
There exist embeddings 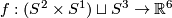 and
and 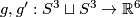 such that the componentwise embedded connected sum
such that the componentwise embedded connected sum 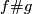 is isotopic to
is isotopic to 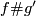 but
but  is not isotopic to
is not isotopic to 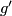 .
.
For an unpublished generalization of Theorem 6.3 and Corollary 6.4 see [Avvakumov2017].
7 Reduction to the case with unknotted components
In this section we assume that 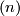 is an
is an  -tuple such that
-tuple such that 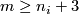 .
.
Define 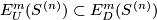 to be the subgroup of links all whose components are unknotted, i.e. isotopic to the standard embedding
to be the subgroup of links all whose components are unknotted, i.e. isotopic to the standard embedding 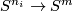 . We remark that
. We remark that 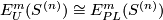 [Haefliger1966a,
[Haefliger1966a,  2.4, 2.6 and 9.3], [Crowley&Ferry&Skopenkov2011,
2.4, 2.6 and 9.3], [Crowley&Ferry&Skopenkov2011,  1.5].
1.5].
Define the restriction homomorphism by mapping the isotopy class of a link to the ordered  -tuple of the isotopy classes of its components:
-tuple of the isotopy classes of its components:
![\displaystyle r \colon E^m_D(S^{(n)}) \to \bigoplus_{i=1}^s E^m_D(S^{n_i}), \quad r[f]:=\oplus_{i=1}^s [f|_{S^{n_i}} \colon S^{n_i} \to S^m].](/images/math/2/5/d/25d2ec311c8371fe4ac42f34989c9ad0.png)
Take  pairwise disjoint
pairwise disjoint  -discs in
-discs in  , i.e. take an embedding
, i.e. take an embedding 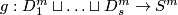 . Define
. Define
![\displaystyle j \colon \bigoplus_{i=1}^s E^m_D(S^{n_i}) \to E^m_D(S^{(n)})\quad\text{by}\quad j([f_1], \ldots, [f_s]):=[(g\circ\sqcup_{i=1}^s f_i):S^{(n)}\to S^m].](/images/math/3/2/9/329c5a3b46fae2defd6d32e45fb15014.png)
Then  is a right inverse of the restriction homomorphism
is a right inverse of the restriction homomorphism  , i.e.
, i.e. 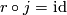 .
The unknotting homomorphism
.
The unknotting homomorphism  is defined to be the homomorphism
is defined to be the homomorphism
Informally, the homomorphism  is obtained by taking embedded connected sums of components with knots
is obtained by taking embedded connected sums of components with knots  representing the elements of
representing the elements of 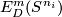 inverse to the components, whose images
inverse to the components, whose images 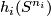 are small and are close to the components.
are small and are close to the components.
For some information on the groups 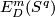 see [Skopenkov2016s], [Skopenkov2006,
see [Skopenkov2016s], [Skopenkov2006,  3.3].
3.3].
8 Classification beyond the metastable range
Theorem 8.1.
[Haefliger1966a, Theorem 10.7], [Skopenkov2009, Theorem 1.1], [Skopenkov2006b, Theorem 1.1]
If 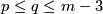 and
and 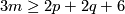 , then there is a homomorphism
, then there is a homomorphism 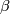 for which the following map is an isomorphism
for which the following map is an isomorphism
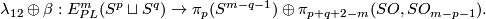
The map 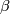 and its right inverse
and its right inverse 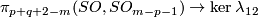 are constructed in [Haefliger1966a,
are constructed in [Haefliger1966a,  10] and in [Haefliger1966, 8.13], respectively. For alternative geometric (and presumably equivalent) definitions of
10] and in [Haefliger1966, 8.13], respectively. For alternative geometric (and presumably equivalent) definitions of 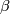 see [Skopenkov2009,
see [Skopenkov2009,  3], [Skopenkov2006b,
3], [Skopenkov2006b,  5], cf. [Skopenkov2007,
5], cf. [Skopenkov2007,  2] and [Crowley&Skopenkov2016,
2] and [Crowley&Skopenkov2016,  2.3]. For a historical remark see [Skopenkov2009, the second paragraph in p. 2].
2.3]. For a historical remark see [Skopenkov2009, the second paragraph in p. 2].
Remark 8.2.
(a) Theorem 8.1 implies that for any 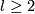 we have an isomorphism
we have an isomorphism
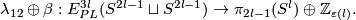
(b) For any 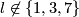 , the map
, the map
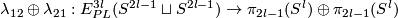
is injective and its image is 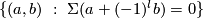 .
.
For  see [Haefliger1962t,
see [Haefliger1962t,  6]. The following proof for
6]. The following proof for 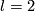 and general remark are intended for specialists.
and general remark are intended for specialists.
For 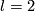 there is an exact sequence
there is an exact sequence 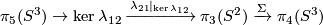 ,
where
,
where 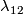 is
is 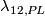 [Haefliger1966a, Corollary 10.3].
We have
[Haefliger1966a, Corollary 10.3].
We have 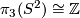 ,
, 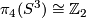 and
and  is the reduction modulo 2.
By the exactness of the previous sequence,
is the reduction modulo 2.
By the exactness of the previous sequence, 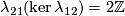 .
By (a)
.
By (a) 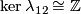 .
Hence
.
Hence  is injective.
We have
is injective.
We have 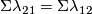 by [Haefliger1966a, Proposition 10.2].
So the formula of (b) follows.
by [Haefliger1966a, Proposition 10.2].
So the formula of (b) follows.
Analogously to [Skopenkov2009, Theorem 3.5] using geometric definitons of 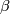 [Skopenkov2009,
[Skopenkov2009,  3], [Skopenkov2006b,
3], [Skopenkov2006b,  5] and geomeric interpretation of the EHP sequence
5] and geomeric interpretation of the EHP sequence 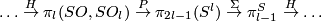 [Koschorke&Sanderson1977, Main Theorem in
[Koschorke&Sanderson1977, Main Theorem in  1] one can possibly prove that
1] one can possibly prove that 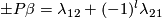 . Then (b) would follow.
. Then (b) would follow.
(c) For any 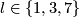 the map
the map 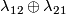 in (b) above is not injective [Haefliger1962t,
in (b) above is not injective [Haefliger1962t,  6].
6].
Theorem 8.3.
For any 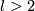 there an isomorphism
there an isomorphism
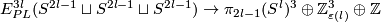
which is the sum of 3 pairwise invariants of Remark 8.2.a, and the triple linking number ( 5).
5).
This follows from [Haefliger1966a, Theorem 9.4], see also [Haefliger1962t,  6].
6].
9 Classification in codimension at least 3
In this section we assume that 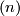 is an
is an  -tuple such that
-tuple such that 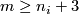 .
For this case a readily calculable classification of
.
For this case a readily calculable classification of 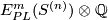 was obtained in
[Crowley&Ferry&Skopenkov2011, Theorem 1.9]. In particular, [Crowley&Ferry&Skopenkov2011,
was obtained in
[Crowley&Ferry&Skopenkov2011, Theorem 1.9]. In particular, [Crowley&Ferry&Skopenkov2011,  1.2] contains necessary and sufficient conditions on
1.2] contains necessary and sufficient conditions on 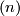 which determine when
which determine when 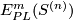 is finite. These results are elementary, but the precise formulations are technical. Hence, we only state the following corollary of [Crowley&Ferry&Skopenkov2011, Theorem 1.9 and
is finite. These results are elementary, but the precise formulations are technical. Hence, we only state the following corollary of [Crowley&Ferry&Skopenkov2011, Theorem 1.9 and  1.2] and describe the methods of its proof in Definition 9.2 and Theorem 9.3 below.
1.2] and describe the methods of its proof in Definition 9.2 and Theorem 9.3 below.
Theorem 9.1. There are algorithms which for integers 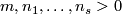
Tex syntax error.
(b) determine whether 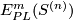 is finite.
is finite.
Definition 9.2 (The Haefliger link sequence). In [Haefliger1966a, 1.2-1.5] Haefliger defined a long exact sequence of abelian groups
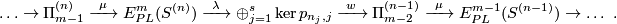
We briefly define the groups and homomorphisms in this sequence, refering to [Haefliger1966a, 1.4] for details.
We first note that in the sequence above the  -tuples
-tuples 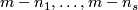 are the same for different terms.
Denote
are the same for different terms.
Denote 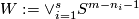 .
For any
.
For any 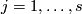 and positive integer
and positive integer  denote by
denote by 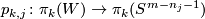 the homomorphism induced by the collapse map onto to the
the homomorphism induced by the collapse map onto to the  -component of the wedge. Denote
-component of the wedge. Denote 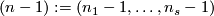 and
and 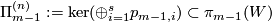 .
.
It can be shown that each component of a link 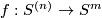 has a non-zero normal vector field. So each component of a link can be pushed off along such a vector field into the complement
has a non-zero normal vector field. So each component of a link can be pushed off along such a vector field into the complement 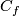 . Analogously to Definition 3.1 there is a canonical homotopy equivalence
. Analogously to Definition 3.1 there is a canonical homotopy equivalence 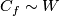 . It can also be shown that the homotopy class in
. It can also be shown that the homotopy class in 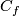 of the push off of the
of the push off of the  th component gives a well-defined map
th component gives a well-defined map 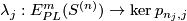 . In fact, the map
. In fact, the map 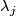 is a generalization of the linking coefficient. Finally, define
is a generalization of the linking coefficient. Finally, define 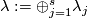 .
.
Taking the Whitehead product with the class of the inclusion of 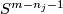 into
into  defines a homomorphism
defines a homomorphism 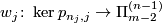 . Define
. Define 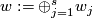 .
.
The definition of the homomorphism 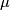 is given in [Haefliger1966a, 1.5].
is given in [Haefliger1966a, 1.5].
Theorem 9.3. (a) [Haefliger1966a, Theorem 1.3] The Haefliger link sequence is exact.
(b) The map 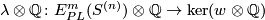 is an isomorphism.
is an isomorphism.
Part (b) follows because 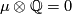 [Crowley&Ferry&Skopenkov2011, Lemma 1.3], and so the Haefliger link sequence after tensoring with the rational numbers
[Crowley&Ferry&Skopenkov2011, Lemma 1.3], and so the Haefliger link sequence after tensoring with the rational numbers 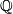 splits into short exact sequences.
splits into short exact sequences.
In general, the computation of the groups and homomorphisms appearing in Theorem 9.3 is difficult. For (a) no computations are known except for those giving (b) and those giving Theorem 8.1 for  (note that Theorem 8.1 has a direct proof easier than proof of Theorem 9.3.a). For (b) the computations constitute most of [Crowley&Ferry&Skopenkov2011]. Hence Theorem 9.3 is not a readily calculable classification in general.
(note that Theorem 8.1 has a direct proof easier than proof of Theorem 9.3.a). For (b) the computations constitute most of [Crowley&Ferry&Skopenkov2011]. Hence Theorem 9.3 is not a readily calculable classification in general.
10 References
- [Avvakumov2016] S. Avvakumov, The classification of certain linked 3-manifolds in 6-space, Moscow Mathematical Journal, 16:1 (2016) 1-25. http://arxiv.org/abs/1408.3918.
- [Avvakumov2017] S. Avvakumov, The classification of linked 3-manifolds in 6-space, Algebraic & Geometric Topology, to appear. arxiv preprint.
- [Crowley&Ferry&Skopenkov2011] D. Crowley, S.C. Ferry, M. Skopenkov, The rational classification of links of codimension >2, Forum Math. 26 (2014), 239-269. https://arxiv.org/abs/1106.1455
- [Crowley&Skopenkov2016] D. Crowley and A. Skopenkov, Embeddings of non-simply-connected 4-manifolds in 7-space, I. Classification modulo knots, Moscow Math. J., 21 (2021), 43--98. arXiv:1611.04738.
- [Haefliger1962] A. Haefliger, Knotted
 -spheres in
-spheres in  -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [HaefligerSteer1965] A. Haefliger and B. Steer, Symmetry of linking coefficients, Comment. Math. Helv., 39 (1965), 259--270.pdf
- [Ivansic&Horvatic1974] I. Ivan\v{s}i\'c and K. Horvati\'c, On unlinking of polyhedra, Glasnik Mat. 9(29) (1974) 147-153.
- [Kervaire1959a] M. Kervaire, An interpretation of G. Whitehead's generalization of H. Hopf's invariant, Ann. of Math. 62 (1959) 345--362.
- [Koschorke&Sanderson1977] U. Koschorke and B. Sanderson, Geometric interpretation of the generalized Hopf invariant, Math. Scand. 41 (1977) 199--217.
- [Koschorke1988] U. Koschorke, Link maps and the geometry of their invariants, Manuscripta Math. 61:4 (1988) 383--415.
- [Massey1968] W. S. Massey, Higher order linking numbers, Proc. Conf. on Algebraic Topology, Univ. Illinois, Chicago Circle, Chicago, Ill., (1968) pp. 174--205. MR0254832 (40 #8039), see also MR1625365 (99e:57016) massey.pdf.
- [Massey1990] W. S. Massey, Homotopy classification of 3-component links of codimension greater than 2, Topol. Appl. 34 (1990) 269--300.
- [Skopenkov2000] A. Skopenkov, On the generalized Massey-Rolfsen invariant for link maps, Fund. Math. 165 (2000), 1-15.
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2006a] A. Skopenkov, Classification of embeddings below the metastable dimension. Available at the arXiv:0607422.
- [Skopenkov2006b] M. Skopenkov, A formula for the group of links in the 2-metastable dimension, arxiv:math/0610320v1
- [Skopenkov2007] A. Skopenkov, A new invariant and parametric connected sum of embeddings, Fund. Math. 197 (2007), 253–269. arXiv:math/0509621. MR2365891 (2008k:57044) Zbl 1145.57019
- [Skopenkov2009] M. Skopenkov, Suspension theorems for links and link maps. Proc. AMS 137 (2009) 359--369. arxiv:math/0610320, version 2 or higher
- [Skopenkov2015] M. Skopenkov, When is the set of embeddings finite up to isotopy? Intern. J. Math. 26:7 (2015), http://arxiv.org/abs/1106.1878
- [Skopenkov2015a] A. Skopenkov, A classification of knotted tori, Proc. A of the Royal Society of Edinburgh, 150:2 (2020), 549-567. Full version: http://arxiv.org/abs/1502.04470
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016e] A. Skopenkov, Embeddings just below the stable range: classification, to appear in Bull. Man. Atl.
- [Skopenkov2016i] A. Skopenkov, Isotopy, submitted to Bull. Man. Atl.
- [Skopenkov2016k] A. Skopenkov, Knotted tori, preprint.
- [Skopenkov2016s] A. Skopenkov, Knots, i.e. embeddings of spheres, preprint.
- [Skopenkov2016t] A. Skopenkov, 3-manifolds in 6-space, to appear in Boll. Man. Atl.
- [Skopenkov2020e] A. Skopenkov, Extendability of simplicial maps is undecidable, Discr. Comp. Geom., 69:1 (2023), 250–259. arXiv:2008.00492
- [Zeeman1962] E. C. Zeeman, Isotopies and knots in manifolds, Topology of 3-manifolds and related topics (Proc. The Univ. of Georgia Institute, 1961), Prentice-Hall (1962), 187–193. MR0140097 (25 #3520) Zbl 1246.57069