Embeddings just below the stable range: classification
| This page has been accepted for publication in the Bulletin of the Manifold Atlas. |
Contents |
1 Introduction
Recall the unknotting theorem that if  is a connected manifold of dimension
is a connected manifold of dimension  , then there is just one isotopy class of embedding
, then there is just one isotopy class of embedding 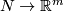 if
if 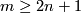 . In this page we summarise the situation for
. In this page we summarise the situation for 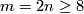 , and give references to the case
, and give references to the case 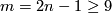 .
.
For notation and conventions see high codimension embeddings.
2 Classification
Classification Theorem 2.1.
Let  be a closed connected
be a closed connected  -manifold. The Whitney invariant
-manifold. The Whitney invariant
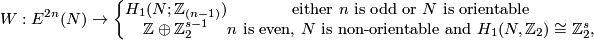
is bijective if either 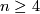 or
or  and CAT=PL [Haefliger&Hirsch1963], [Bausum1975], [Vrabec1977], cf. [Hudson1969]
and CAT=PL [Haefliger&Hirsch1963], [Bausum1975], [Vrabec1977], cf. [Hudson1969]
The Whitney invariant is defined below.
The classification of smooth embeddings of 3-manifolds in 6-space is more complicated. For analogous classification of 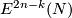 see Embeddings of highly-connected manifolds. Some estimations of
see Embeddings of highly-connected manifolds. Some estimations of 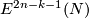 for a closed
for a closed  -connected
-connected  -manifold
-manifold  and
and 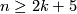 (including
(including 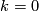 ) are presented in [Skopenkov2010]. See also Embeddings of 4-manifolds in 7-space.
) are presented in [Skopenkov2010]. See also Embeddings of 4-manifolds in 7-space.
3 Examples
Together with the Haefliger knotted sphere 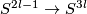 , Hudson's examples were the first examples of embeddings in codimension greater than 2 not isotopic to the standard embedding. (Hudson's construction [Hudson1963] was not as explicit as the one below).
, Hudson's examples were the first examples of embeddings in codimension greater than 2 not isotopic to the standard embedding. (Hudson's construction [Hudson1963] was not as explicit as the one below).
For 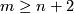 define the
define the 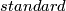
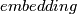
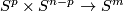 as the composition
as the composition 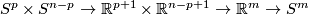 of standard embeddings.
of standard embeddings.
3.1 Hudson tori 1
In this subsection, we recall for 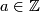 and
and  . Hudson's construction of embedings
. Hudson's construction of embedings
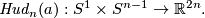
Take the standard embeddings 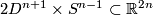 (where
(where  means homothety with coefficient 2) and
means homothety with coefficient 2) and
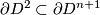 .
Fix a point
.
Fix a point 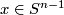 .
The Hudson torus
.
The Hudson torus 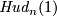 is the embedded connected sum of
is the embedded connected sum of
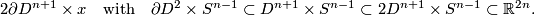
(Unlike the connected sum mentioned in embedded conntected sum this is a `linked' connected sum, i.e. connected sum of two embeddings whose images are not contained in disjoint cubes.)
For 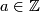 instead of an embedded
instead of an embedded  -sphere
-sphere 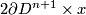 we can take
we can take  copies
copies 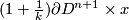 (
(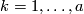 ) of
) of  -sphere outside
-sphere outside 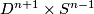 `parallel' to
`parallel' to
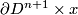 .
Then we join these spheres by tubes so that the homotopy class of the resulting embedding
.
Then we join these spheres by tubes so that the homotopy class of the resulting embedding
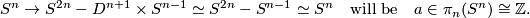
Let  be the connected sum of this embedding with the above standard
embedding
be the connected sum of this embedding with the above standard
embedding 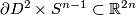 .
.
Clearly, 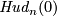 is isotopic to the standard embedding.
is isotopic to the standard embedding.
Proposition 3.1.
For  odd
odd  is isotopic to
is isotopic to 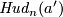 if and only
if
if and only
if 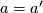 .
.
For 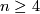 even
even  is isotopic to
is isotopic to 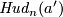 if and only if
if and only if
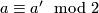 .
.
In particular, 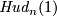 is not isotopic to
is not isotopic to 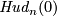 for each
for each  (this was the original motivation for Hudson).
(this was the original motivation for Hudson).
Proposition 3.1 follows by Remark 5.e and, for  even, by Theorem 4, both results from classification just below the stable range.
even, by Theorem 4, both results from classification just below the stable range.
It would be interesting to find an explicit construction of an isotopy between
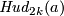 and
and 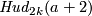 (cf. [Vrabec1977], \S6) and to prove the analogue of
Proposition 3.1 for
(cf. [Vrabec1977], \S6) and to prove the analogue of
Proposition 3.1 for  .
.
3.2 Hudson tori 2
In this subsection we give, for 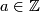 and
and  another construction of embeddings
another construction of embeddings
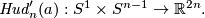
Define a map  to be the constant
to be the constant 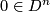 on one
component
on one
component 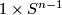 and the standard embedding
and the standard embedding
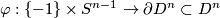 on the other component.
This map gives an
on the other component.
This map gives an 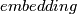
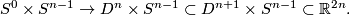
(See Figure 2.2 of [Skopenkov2006].)
Each disk 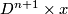 intersects the image of this embedding at two
points lying in
intersects the image of this embedding at two
points lying in 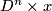 .
Extend this embedding
.
Extend this embedding 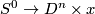 for each
for each 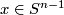 to an
embedding
to an
embedding 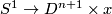 .
(See Figure 2.3 of [Skopenkov2006].)
Thus we obtain the Hudson torus
.
(See Figure 2.3 of [Skopenkov2006].)
Thus we obtain the Hudson torus
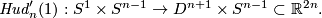
The embedding 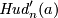 is obtained in the same way starting from a map
is obtained in the same way starting from a map
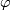 of degree
of degree  .
.
The same proposition as above holds with 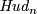 replaced to
replaced to 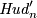 .
.
3.3 Remarks
We have  is PL isotopic to
is PL isotopic to 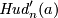 [Skopenkov2006a].
It would be interesting to prove the smooth analogue of this result.
[Skopenkov2006a].
It would be interesting to prove the smooth analogue of this result.
For  these construction give what we call the
these construction give what we call the 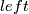 Hudson torus.
The
Hudson torus.
The 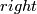 Hudson torus is constructed analogously and is the
composition of the left Hudson torus and the exchanging factors
autodiffeomorphism of
Hudson torus is constructed analogously and is the
composition of the left Hudson torus and the exchanging factors
autodiffeomorphism of 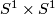 .
.
Analogously one constructs the Hudson torus 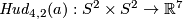 for
for 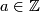 or, more generally,
or, more generally, 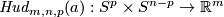 for
for 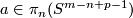 and
and 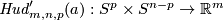 for
for 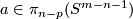 .
.
3.4 An action of the first homology group on embeddings
In this subsection, for 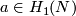 and for orientable
and for orientable  with
with  , we construct an embedding
, we construct an embedding 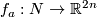 from an embedding
from an embedding 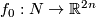 .
.
For 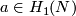 , represent
, represent  by an embedding
by an embedding 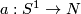 . Since any orientable bundle over
. Since any orientable bundle over  is trivial,
is trivial, 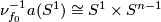 . Identify
. Identify 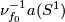 with
with 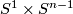 . It remains to make an embedded surgery of
. It remains to make an embedded surgery of
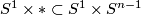 to obtain an
to obtain an  -sphere
-sphere 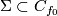 , and then we set
, and then we set 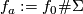 .
.
Take a vector field on 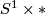 normal to
normal to 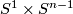 . Extend
. Extend 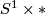 along this vector field to a smooth map
along this vector field to a smooth map
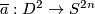 . Since
. Since 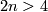 and
and 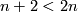 , by general position we may assume that
, by general position we may assume that 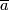 is an embedding and
is an embedding and 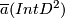 misses
misses 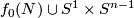 . Since
. Since 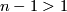 , we have
, we have 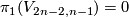 .
Hence the standard framing of
.
Hence the standard framing of 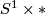 in
in 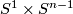 extends to an
extends to an  -framing on
-framing on 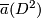 in
in  .
Thus
.
Thus  extends to an embedding
extends to an embedding

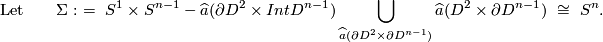
This construction generalizes the construction of  (from
(from 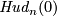 ).
).
Clearly, 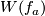 is
is  or
or  . Thus unless
. Thus unless  and CAT=DIFF
and CAT=DIFF
- all isotopy classes of embedings
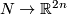 can be obtained (from a certain given embedding
can be obtained (from a certain given embedding  ) by the above construction;
) by the above construction;
- the above construction defines an action
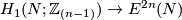 .
.
4 The Whitney invariant (for either n odd or N orientable)
Fix orientations on  and, if
and, if  is even, on
is even, on  . Fix an embedding
. Fix an embedding 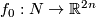 . For an embedding
. For an embedding 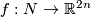 the restrictions of
the restrictions of  and
and  to
to  are regular homotopic [Hirsch1959]. Since
are regular homotopic [Hirsch1959]. Since  has an
has an  -dimensional spine, it follows that these restrictions are isotopic, cf. [Haefliger&Hirsch1963], 3.1.b, [Takase2006], Lemma 2.2. So we can make an isotopy of
-dimensional spine, it follows that these restrictions are isotopic, cf. [Haefliger&Hirsch1963], 3.1.b, [Takase2006], Lemma 2.2. So we can make an isotopy of  and assume that
and assume that 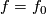 on
on  . Take a general position homotopy
. Take a general position homotopy 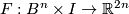 relative to
relative to
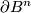 between the restrictions of
between the restrictions of  and
and  to
to  . Then
. Then 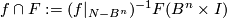 (i.e. `the intersection of this homotopy with
(i.e. `the intersection of this homotopy with 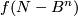 ') is a 1-manifold (possibly non-compact) without boundary. Define
') is a 1-manifold (possibly non-compact) without boundary. Define 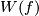 to be the homology class of the closure of this 1-manifold:
to be the homology class of the closure of this 1-manifold:
![\displaystyle W(f):=[Cl(f\cap F)]\in H_1(N_0,\partial N_0;\Zz_{(n)})\cong H_1(N;\Zz_{(n)}).](/images/math/2/b/b/2bbc331d0f1495918467d3ff52161652.png)
The orientation on  is defined for
is defined for  orientable as follows. (This orientation is defined for each
orientable as follows. (This orientation is defined for each  but used only for odd
but used only for odd  .) For each point
.) For each point 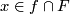 take a vector at
take a vector at  tangent to
tangent to  . Complete this vector to a positive base tangent to
. Complete this vector to a positive base tangent to  . Since
. Since 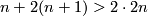 , by general position there is a unique point
, by general position there is a unique point 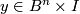 such that
such that 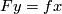 . The tangent vector at
. The tangent vector at  thus gives a tangent vector at
thus gives a tangent vector at  to
to 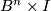 . Complete this vector to a positive base tangent to
. Complete this vector to a positive base tangent to 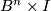 , where the orientation on
, where the orientation on  comes from
comes from  . The union of the images of the constructed two bases is a base at
. The union of the images of the constructed two bases is a base at 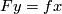 of
of  . If this base is positive, then call the initial vector of
. If this base is positive, then call the initial vector of  positive. Since a change of the orientation on
positive. Since a change of the orientation on  forces a change of the orientation of the latter base of
forces a change of the orientation of the latter base of  , it follows that this condition indeed defines an orientation on
, it follows that this condition indeed defines an orientation on  .
.
Remark 4.1.
- The Whitney invariant is well-defined, i.e. independent of the choice of
 and of the isotopy making
and of the isotopy making 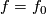 outside
outside  . This is so because the above definition is clearly equivalent to the following:
. This is so because the above definition is clearly equivalent to the following: 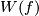 is the homology class of the algebraic sum of the top-dimensional simplices of the self-intersection set
is the homology class of the algebraic sum of the top-dimensional simplices of the self-intersection set 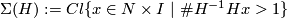 of a general position homotopy
of a general position homotopy  between
between  and
and  . (For details and definition of the signs of the simplices see [Hudson1969], \S12, [Vrabec1977], p. 145, [Skopenkov2006], \S2, [Skopenkov2010].) It is for being well-defined that we need
. (For details and definition of the signs of the simplices see [Hudson1969], \S12, [Vrabec1977], p. 145, [Skopenkov2006], \S2, [Skopenkov2010].) It is for being well-defined that we need  -coefficients when
-coefficients when  is even.
is even.
- Clearly,
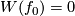 . The definition of
. The definition of  depends on the choice of
depends on the choice of  , but we write
, but we write  not
not 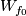 for brevity.
for brevity.
- Since a change of the orientation on
 forces a change of the orientation on
forces a change of the orientation on  , the class
, the class 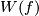 is independent of the choice of the orientation on
is independent of the choice of the orientation on  . For the reflection
. For the reflection 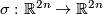 with respect to a hyperplane we have
with respect to a hyperplane we have 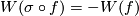 (because we may assume that
(because we may assume that 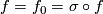 on
on  and because a change of the orientation of
and because a change of the orientation of  forces a change of the orientation of
forces a change of the orientation of  ).
).
- The above definition makes sense for each
 , not only for
, not only for  .
.
- Clearly,
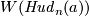 is
is  or
or  for
for  for the Hudson tori.
for the Hudson tori.
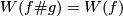 for each embeddings
for each embeddings 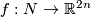 and
and 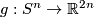 .
.
5 A generalization to highly-connected manifolds
Examples are the above Hudson tori 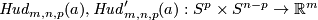 . See also [Milgram&Rees1971].
. See also [Milgram&Rees1971].
5.1 Classification
Theorem 5.1. Let  be a closed orientable homologically
be a closed orientable homologically  -connected
-connected  -manifold,
-manifold, 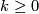 . Then the Whitney invariant
. Then the Whitney invariant
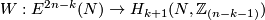
is a bijection, provided 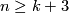 or
or 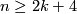 in the PL or DIFF categories, respectively.
in the PL or DIFF categories, respectively.
Theorem 5.1 was proved in [Haefliger&Hirsch1963], [Hudson1969], \S11, [Boechat&Haefliger1970], [Boechat1971], [Vrabec1977] 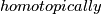
 -connected manifolds. The proof works for
-connected manifolds. The proof works for 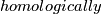
 -connected manifolds.
-connected manifolds.
E.g. by Theorem 5.1 we obtain that the Whitney invariant 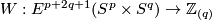 is bijective for
is bijective for 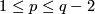 .
It is in fact a group isomorphism; the generator is the Hudson torus.
.
It is in fact a group isomorphism; the generator is the Hudson torus.
The PL case of Theorem 5.1 gives nothing but the Unknotting Spheres Theorem for 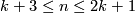 .
.
Analogously to Theorem 5.1 it may be proved that
- if
 is a closed connected non-orientable
is a closed connected non-orientable  -manifold, then
-manifold, then
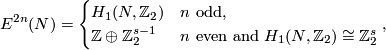
provided  or
or  in the PL or DIFF categories, respectively.
in the PL or DIFF categories, respectively.
This is proved in [Haefliger1962b], [Weber1967], [Bausum1975], [Vrabec1977] (a minor miscalculation being corrected only in [Vrabec1977]).
Because of the existence of knots the analogues of Theorem 5.1 for 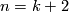 in the PL case, and for
in the PL case, and for 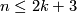 in the smooth case are false. So for the smooth category and
in the smooth case are false. So for the smooth category and 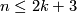 a classification is much harder: for 40 years the
a classification is much harder: for 40 years the  known concrete complete classification results were for spheres. The following result was obtained using the Kreck modification of surgery theory.
known concrete complete classification results were for spheres. The following result was obtained using the Kreck modification of surgery theory.
Theorem 5.2. [Skopenkov2006] Let  be a closed homologically
be a closed homologically 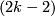 -connected
-connected  -manifold. Then the Whitney invariant
-manifold. Then the Whitney invariant 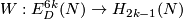 is surjective and for each
is surjective and for each 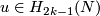 there is a 1--1 correspondence
there is a 1--1 correspondence
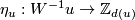 , where
, where 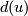 is the divisibility of the projection of
is the divisibility of the projection of  to the free part of
to the free part of 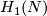 .
.
Recall that the divisibility of zero is zero and the divisibility of 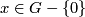 is
is 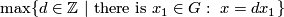 . E.g. by Theorem 5.2 we obtain that
. E.g. by Theorem 5.2 we obtain that
- the Whitney invariant
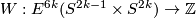 is surjective and for each
is surjective and for each 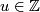 there is a 1--1 correspondence
there is a 1--1 correspondence 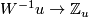 .
.
5.2 The Whitney invariant
6 References
- [Bausum1975] D. R. Bausum, Embeddings and immersions of manifolds in Euclidean space, Trans. Amer. Math. Soc. 213 (1975), 263–303. MR0474330 (57 #13976) Zbl 0323.57017
- [Boechat&Haefliger1970] J. Boéchat and A. Haefliger, Plongements différentiables des variétés orientées de dimension
 dans
dans 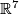 , (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
, (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
- [Boechat1971] J. Boéchat, Plongements de variétées différentiables orientées de dimension
 dans
dans 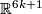 , Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
, Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
- [Haefliger&Hirsch1963] A. Haefliger and M. W. Hirsch, On the existence and classification of differentiable embeddings, Topology 2 (1963), 129–135. see also MR0149494 (26 #6981) Zbl 0113.38607
- [Haefliger1962b] A. Haefliger, Plongements de variétés dans le domain stable, Séminaire Bourbaki, 245 (1962).
- [Hirsch1959] M. W. Hirsch, Immersions of manifolds, Trans. Amer. Math. Soc. 93 (1959), 242–276. MR0119214 (22 #9980) Zbl 0118.18603
- [Hudson1963] J. F. P. Hudson, Knotted tori, Topology 2 (1963), 11–22. MR0146829 (26 #4349) Zbl 0151.32503
- [Hudson1969] J. F. P. Hudson, Piecewise linear topology, W. A. Benjamin, Inc., New York-Amsterdam, 1969. MR0248844 (40 #2094) Zbl 0189.54507
- [Milgram&Rees1971] R. Milgram and E. Rees, On the normal bundle to an embedding., Topology 10 (1971), 299-308. MR0290391 (44 #7572) Zbl 0207.22302
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2006a] A. Skopenkov, Classification of embeddings below the metastable dimension. Available at the arXiv:0607422.
- [Skopenkov2010] A. Skopenkov, Embeddings of k-connected n-manifolds into
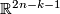 , Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
, Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
- [Takase2006] M. Takase, Homology 3-spheres in codimension three, Internat. J. Math. 17 (2006), no.8, 869–885.
arxiv:math/0506464 MR2261638 (2007g:57049) Zbl 1113.57013
- [Vrabec1977] J. Vrabec, Knotting a
 -connected closed
-connected closed 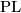
 -manifold in
-manifold in 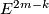 , Trans. Amer. Math. Soc. 233 (1977), 137–165. MR0645405 (58 #31097) Zbl 386.57013
, Trans. Amer. Math. Soc. 233 (1977), 137–165. MR0645405 (58 #31097) Zbl 386.57013
- [Weber1967] C. Weber, Plongements de polyedres dans le domaine metastable, Comment. Math. Helv. 42 (1967), 1-27. MR0238330 (38 #6606) Zbl 0152.22402
|
This page has not been refereed. The information given here might be incomplete or provisional. |
 , then there is just one isotopy class of embedding
, then there is just one isotopy class of embedding 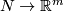 if
if 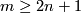 . In this page we summarise the situation for
. In this page we summarise the situation for 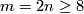 , and give references to the case
, and give references to the case 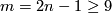 .
.
For notation and conventions see high codimension embeddings.
2 Classification
Classification Theorem 2.1.
Let  be a closed connected
be a closed connected  -manifold. The Whitney invariant
-manifold. The Whitney invariant
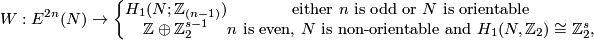
is bijective if either 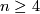 or
or  and CAT=PL [Haefliger&Hirsch1963], [Bausum1975], [Vrabec1977], cf. [Hudson1969]
and CAT=PL [Haefliger&Hirsch1963], [Bausum1975], [Vrabec1977], cf. [Hudson1969]
The Whitney invariant is defined below.
The classification of smooth embeddings of 3-manifolds in 6-space is more complicated. For analogous classification of 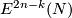 see Embeddings of highly-connected manifolds. Some estimations of
see Embeddings of highly-connected manifolds. Some estimations of 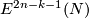 for a closed
for a closed  -connected
-connected  -manifold
-manifold  and
and 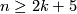 (including
(including 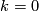 ) are presented in [Skopenkov2010]. See also Embeddings of 4-manifolds in 7-space.
) are presented in [Skopenkov2010]. See also Embeddings of 4-manifolds in 7-space.
3 Examples
Together with the Haefliger knotted sphere 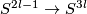 , Hudson's examples were the first examples of embeddings in codimension greater than 2 not isotopic to the standard embedding. (Hudson's construction [Hudson1963] was not as explicit as the one below).
, Hudson's examples were the first examples of embeddings in codimension greater than 2 not isotopic to the standard embedding. (Hudson's construction [Hudson1963] was not as explicit as the one below).
For 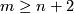 define the
define the 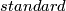
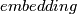
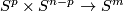 as the composition
as the composition 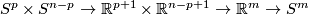 of standard embeddings.
of standard embeddings.
3.1 Hudson tori 1
In this subsection, we recall for 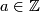 and
and  . Hudson's construction of embedings
. Hudson's construction of embedings
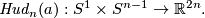
Take the standard embeddings 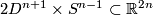 (where
(where  means homothety with coefficient 2) and
means homothety with coefficient 2) and
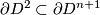 .
Fix a point
.
Fix a point 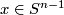 .
The Hudson torus
.
The Hudson torus 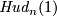 is the embedded connected sum of
is the embedded connected sum of
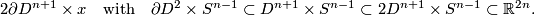
(Unlike the connected sum mentioned in embedded conntected sum this is a `linked' connected sum, i.e. connected sum of two embeddings whose images are not contained in disjoint cubes.)
For  instead of an embedded
instead of an embedded  -sphere
-sphere 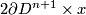 we can take
we can take  copies
copies 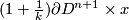 (
(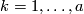 ) of
) of  -sphere outside
-sphere outside 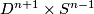 `parallel' to
`parallel' to
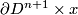 .
Then we join these spheres by tubes so that the homotopy class of the resulting embedding
.
Then we join these spheres by tubes so that the homotopy class of the resulting embedding
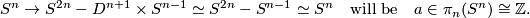
Let  be the connected sum of this embedding with the above standard
embedding
be the connected sum of this embedding with the above standard
embedding 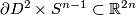 .
.
Clearly, 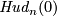 is isotopic to the standard embedding.
is isotopic to the standard embedding.
Proposition 3.1.
For  odd
odd  is isotopic to
is isotopic to 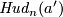 if and only
if
if and only
if 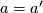 .
.
For 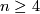 even
even  is isotopic to
is isotopic to 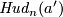 if and only if
if and only if
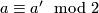 .
.
In particular, 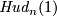 is not isotopic to
is not isotopic to 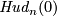 for each
for each  (this was the original motivation for Hudson).
(this was the original motivation for Hudson).
Proposition 3.1 follows by Remark 5.e and, for  even, by Theorem 4, both results from classification just below the stable range.
even, by Theorem 4, both results from classification just below the stable range.
It would be interesting to find an explicit construction of an isotopy between
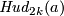 and
and 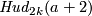 (cf. [Vrabec1977], \S6) and to prove the analogue of
Proposition 3.1 for
(cf. [Vrabec1977], \S6) and to prove the analogue of
Proposition 3.1 for  .
.
3.2 Hudson tori 2
In this subsection we give, for 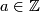 and
and  another construction of embeddings
another construction of embeddings
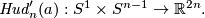
Define a map  to be the constant
to be the constant 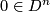 on one
component
on one
component 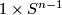 and the standard embedding
and the standard embedding
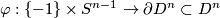 on the other component.
This map gives an
on the other component.
This map gives an 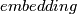
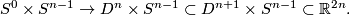
(See Figure 2.2 of [Skopenkov2006].)
Each disk 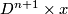 intersects the image of this embedding at two
points lying in
intersects the image of this embedding at two
points lying in 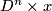 .
Extend this embedding
.
Extend this embedding 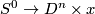 for each
for each 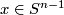 to an
embedding
to an
embedding 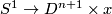 .
(See Figure 2.3 of [Skopenkov2006].)
Thus we obtain the Hudson torus
.
(See Figure 2.3 of [Skopenkov2006].)
Thus we obtain the Hudson torus
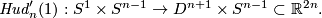
The embedding 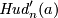 is obtained in the same way starting from a map
is obtained in the same way starting from a map
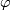 of degree
of degree  .
.
The same proposition as above holds with 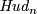 replaced to
replaced to 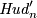 .
.
3.3 Remarks
We have  is PL isotopic to
is PL isotopic to 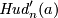 [Skopenkov2006a].
It would be interesting to prove the smooth analogue of this result.
[Skopenkov2006a].
It would be interesting to prove the smooth analogue of this result.
For  these construction give what we call the
these construction give what we call the 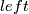 Hudson torus.
The
Hudson torus.
The 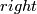 Hudson torus is constructed analogously and is the
composition of the left Hudson torus and the exchanging factors
autodiffeomorphism of
Hudson torus is constructed analogously and is the
composition of the left Hudson torus and the exchanging factors
autodiffeomorphism of 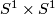 .
.
Analogously one constructs the Hudson torus 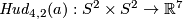 for
for 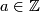 or, more generally,
or, more generally, 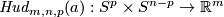 for
for 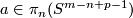 and
and 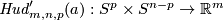 for
for 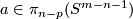 .
.
3.4 An action of the first homology group on embeddings
In this subsection, for 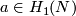 and for orientable
and for orientable  with
with  , we construct an embedding
, we construct an embedding 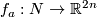 from an embedding
from an embedding 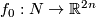 .
.
For 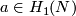 , represent
, represent  by an embedding
by an embedding 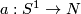 . Since any orientable bundle over
. Since any orientable bundle over  is trivial,
is trivial, 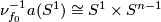 . Identify
. Identify 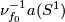 with
with 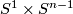 . It remains to make an embedded surgery of
. It remains to make an embedded surgery of
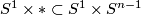 to obtain an
to obtain an  -sphere
-sphere 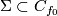 , and then we set
, and then we set 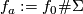 .
.
Take a vector field on 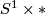 normal to
normal to 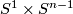 . Extend
. Extend 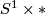 along this vector field to a smooth map
along this vector field to a smooth map
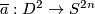 . Since
. Since 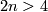 and
and 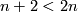 , by general position we may assume that
, by general position we may assume that 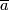 is an embedding and
is an embedding and 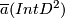 misses
misses 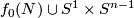 . Since
. Since 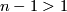 , we have
, we have 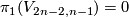 .
Hence the standard framing of
.
Hence the standard framing of 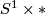 in
in 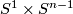 extends to an
extends to an  -framing on
-framing on 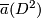 in
in  .
Thus
.
Thus  extends to an embedding
extends to an embedding

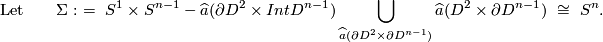
This construction generalizes the construction of  (from
(from 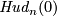 ).
).
Clearly, 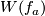 is
is  or
or  . Thus unless
. Thus unless  and CAT=DIFF
and CAT=DIFF
- all isotopy classes of embedings
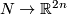 can be obtained (from a certain given embedding
can be obtained (from a certain given embedding  ) by the above construction;
) by the above construction;
- the above construction defines an action
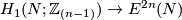 .
.
4 The Whitney invariant (for either n odd or N orientable)
Fix orientations on  and, if
and, if  is even, on
is even, on  . Fix an embedding
. Fix an embedding 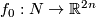 . For an embedding
. For an embedding 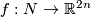 the restrictions of
the restrictions of  and
and  to
to  are regular homotopic [Hirsch1959]. Since
are regular homotopic [Hirsch1959]. Since  has an
has an  -dimensional spine, it follows that these restrictions are isotopic, cf. [Haefliger&Hirsch1963], 3.1.b, [Takase2006], Lemma 2.2. So we can make an isotopy of
-dimensional spine, it follows that these restrictions are isotopic, cf. [Haefliger&Hirsch1963], 3.1.b, [Takase2006], Lemma 2.2. So we can make an isotopy of  and assume that
and assume that 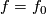 on
on  . Take a general position homotopy
. Take a general position homotopy 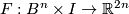 relative to
relative to
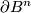 between the restrictions of
between the restrictions of  and
and  to
to  . Then
. Then 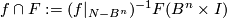 (i.e. `the intersection of this homotopy with
(i.e. `the intersection of this homotopy with 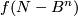 ') is a 1-manifold (possibly non-compact) without boundary. Define
') is a 1-manifold (possibly non-compact) without boundary. Define 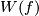 to be the homology class of the closure of this 1-manifold:
to be the homology class of the closure of this 1-manifold:
![\displaystyle W(f):=[Cl(f\cap F)]\in H_1(N_0,\partial N_0;\Zz_{(n)})\cong H_1(N;\Zz_{(n)}).](/images/math/2/b/b/2bbc331d0f1495918467d3ff52161652.png)
The orientation on  is defined for
is defined for  orientable as follows. (This orientation is defined for each
orientable as follows. (This orientation is defined for each  but used only for odd
but used only for odd  .) For each point
.) For each point 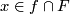 take a vector at
take a vector at  tangent to
tangent to  . Complete this vector to a positive base tangent to
. Complete this vector to a positive base tangent to  . Since
. Since 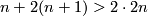 , by general position there is a unique point
, by general position there is a unique point 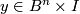 such that
such that 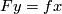 . The tangent vector at
. The tangent vector at  thus gives a tangent vector at
thus gives a tangent vector at  to
to 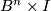 . Complete this vector to a positive base tangent to
. Complete this vector to a positive base tangent to 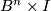 , where the orientation on
, where the orientation on  comes from
comes from  . The union of the images of the constructed two bases is a base at
. The union of the images of the constructed two bases is a base at 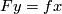 of
of  . If this base is positive, then call the initial vector of
. If this base is positive, then call the initial vector of  positive. Since a change of the orientation on
positive. Since a change of the orientation on  forces a change of the orientation of the latter base of
forces a change of the orientation of the latter base of  , it follows that this condition indeed defines an orientation on
, it follows that this condition indeed defines an orientation on  .
.
Remark 4.1.
- The Whitney invariant is well-defined, i.e. independent of the choice of
 and of the isotopy making
and of the isotopy making 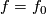 outside
outside  . This is so because the above definition is clearly equivalent to the following:
. This is so because the above definition is clearly equivalent to the following: 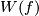 is the homology class of the algebraic sum of the top-dimensional simplices of the self-intersection set
is the homology class of the algebraic sum of the top-dimensional simplices of the self-intersection set 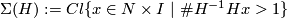 of a general position homotopy
of a general position homotopy  between
between  and
and  . (For details and definition of the signs of the simplices see [Hudson1969], \S12, [Vrabec1977], p. 145, [Skopenkov2006], \S2, [Skopenkov2010].) It is for being well-defined that we need
. (For details and definition of the signs of the simplices see [Hudson1969], \S12, [Vrabec1977], p. 145, [Skopenkov2006], \S2, [Skopenkov2010].) It is for being well-defined that we need  -coefficients when
-coefficients when  is even.
is even.
- Clearly,
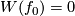 . The definition of
. The definition of  depends on the choice of
depends on the choice of  , but we write
, but we write  not
not 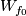 for brevity.
for brevity.
- Since a change of the orientation on
 forces a change of the orientation on
forces a change of the orientation on  , the class
, the class 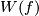 is independent of the choice of the orientation on
is independent of the choice of the orientation on  . For the reflection
. For the reflection 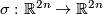 with respect to a hyperplane we have
with respect to a hyperplane we have 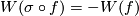 (because we may assume that
(because we may assume that 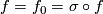 on
on  and because a change of the orientation of
and because a change of the orientation of  forces a change of the orientation of
forces a change of the orientation of  ).
).
- The above definition makes sense for each
 , not only for
, not only for  .
.
- Clearly,
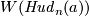 is
is  or
or  for
for  for the Hudson tori.
for the Hudson tori.
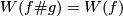 for each embeddings
for each embeddings 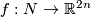 and
and 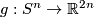 .
.
5 A generalization to highly-connected manifolds
Examples are the above Hudson tori 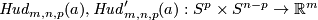 . See also [Milgram&Rees1971].
. See also [Milgram&Rees1971].
5.1 Classification
Theorem 5.1. Let  be a closed orientable homologically
be a closed orientable homologically  -connected
-connected  -manifold,
-manifold, 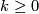 . Then the Whitney invariant
. Then the Whitney invariant
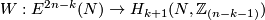
is a bijection, provided 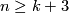 or
or 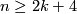 in the PL or DIFF categories, respectively.
in the PL or DIFF categories, respectively.
Theorem 5.1 was proved in [Haefliger&Hirsch1963], [Hudson1969], \S11, [Boechat&Haefliger1970], [Boechat1971], [Vrabec1977] 
 -connected manifolds. The proof works for
-connected manifolds. The proof works for 
 -connected manifolds.
-connected manifolds.
E.g. by Theorem 5.1 we obtain that the Whitney invariant 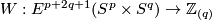 is bijective for
is bijective for 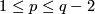 .
It is in fact a group isomorphism; the generator is the Hudson torus.
.
It is in fact a group isomorphism; the generator is the Hudson torus.
The PL case of Theorem 5.1 gives nothing but the Unknotting Spheres Theorem for 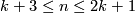 .
.
Analogously to Theorem 5.1 it may be proved that
- if
 is a closed connected non-orientable
is a closed connected non-orientable  -manifold, then
-manifold, then
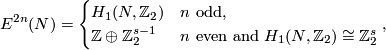
provided  or
or 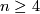 in the PL or DIFF categories, respectively.
in the PL or DIFF categories, respectively.
This is proved in [Haefliger1962b], [Weber1967], [Bausum1975], [Vrabec1977] (a minor miscalculation being corrected only in [Vrabec1977]).
Because of the existence of knots the analogues of Theorem 5.1 for 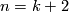 in the PL case, and for
in the PL case, and for 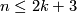 in the smooth case are false. So for the smooth category and
in the smooth case are false. So for the smooth category and 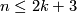 a classification is much harder: for 40 years the
a classification is much harder: for 40 years the 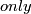 known concrete complete classification results were for spheres. The following result was obtained using the Kreck modification of surgery theory.
known concrete complete classification results were for spheres. The following result was obtained using the Kreck modification of surgery theory.
Theorem 5.2. [Skopenkov2006] Let  be a closed homologically
be a closed homologically 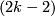 -connected
-connected  -manifold. Then the Whitney invariant
-manifold. Then the Whitney invariant 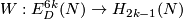 is surjective and for each
is surjective and for each 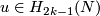 there is a 1--1 correspondence
there is a 1--1 correspondence
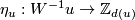 , where
, where 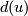 is the divisibility of the projection of
is the divisibility of the projection of  to the free part of
to the free part of 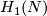 .
.
Recall that the divisibility of zero is zero and the divisibility of 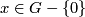 is
is 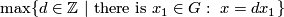 . E.g. by Theorem 5.2 we obtain that
. E.g. by Theorem 5.2 we obtain that
- the Whitney invariant
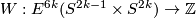 is surjective and for each
is surjective and for each 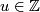 there is a 1--1 correspondence
there is a 1--1 correspondence 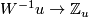 .
.
5.2 The Whitney invariant
6 References
- [Bausum1975] D. R. Bausum, Embeddings and immersions of manifolds in Euclidean space, Trans. Amer. Math. Soc. 213 (1975), 263–303. MR0474330 (57 #13976) Zbl 0323.57017
- [Boechat&Haefliger1970] J. Boéchat and A. Haefliger, Plongements différentiables des variétés orientées de dimension
 dans
dans 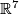 , (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
, (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
- [Boechat1971] J. Boéchat, Plongements de variétées différentiables orientées de dimension
 dans
dans 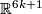 , Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
, Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
- [Haefliger&Hirsch1963] A. Haefliger and M. W. Hirsch, On the existence and classification of differentiable embeddings, Topology 2 (1963), 129–135. see also MR0149494 (26 #6981) Zbl 0113.38607
- [Haefliger1962b] A. Haefliger, Plongements de variétés dans le domain stable, Séminaire Bourbaki, 245 (1962).
- [Hirsch1959] M. W. Hirsch, Immersions of manifolds, Trans. Amer. Math. Soc. 93 (1959), 242–276. MR0119214 (22 #9980) Zbl 0118.18603
- [Hudson1963] J. F. P. Hudson, Knotted tori, Topology 2 (1963), 11–22. MR0146829 (26 #4349) Zbl 0151.32503
- [Hudson1969] J. F. P. Hudson, Piecewise linear topology, W. A. Benjamin, Inc., New York-Amsterdam, 1969. MR0248844 (40 #2094) Zbl 0189.54507
- [Milgram&Rees1971] R. Milgram and E. Rees, On the normal bundle to an embedding., Topology 10 (1971), 299-308. MR0290391 (44 #7572) Zbl 0207.22302
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2006a] A. Skopenkov, Classification of embeddings below the metastable dimension. Available at the arXiv:0607422.
- [Skopenkov2010] A. Skopenkov, Embeddings of k-connected n-manifolds into
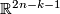 , Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
, Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
- [Takase2006] M. Takase, Homology 3-spheres in codimension three, Internat. J. Math. 17 (2006), no.8, 869–885.
arxiv:math/0506464 MR2261638 (2007g:57049) Zbl 1113.57013
- [Vrabec1977] J. Vrabec, Knotting a
 -connected closed
-connected closed 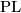
 -manifold in
-manifold in 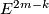 , Trans. Amer. Math. Soc. 233 (1977), 137–165. MR0645405 (58 #31097) Zbl 386.57013
, Trans. Amer. Math. Soc. 233 (1977), 137–165. MR0645405 (58 #31097) Zbl 386.57013
- [Weber1967] C. Weber, Plongements de polyedres dans le domaine metastable, Comment. Math. Helv. 42 (1967), 1-27. MR0238330 (38 #6606) Zbl 0152.22402
|
This page has not been refereed. The information given here might be incomplete or provisional. |
 , then there is just one isotopy class of embedding
, then there is just one isotopy class of embedding 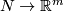 if
if 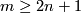 . In this page we summarise the situation for
. In this page we summarise the situation for 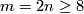 , and give references to the case
, and give references to the case 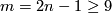 .
.
For notation and conventions see high codimension embeddings.
2 Classification
Classification Theorem 2.1.
Let  be a closed connected
be a closed connected  -manifold. The Whitney invariant
-manifold. The Whitney invariant
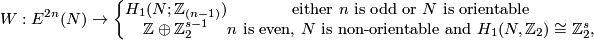
is bijective if either 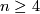 or
or  and CAT=PL [Haefliger&Hirsch1963], [Bausum1975], [Vrabec1977], cf. [Hudson1969]
and CAT=PL [Haefliger&Hirsch1963], [Bausum1975], [Vrabec1977], cf. [Hudson1969]
The Whitney invariant is defined below.
The classification of smooth embeddings of 3-manifolds in 6-space is more complicated. For analogous classification of 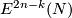 see Embeddings of highly-connected manifolds. Some estimations of
see Embeddings of highly-connected manifolds. Some estimations of 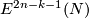 for a closed
for a closed  -connected
-connected  -manifold
-manifold  and
and 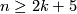 (including
(including 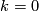 ) are presented in [Skopenkov2010]. See also Embeddings of 4-manifolds in 7-space.
) are presented in [Skopenkov2010]. See also Embeddings of 4-manifolds in 7-space.
3 Examples
Together with the Haefliger knotted sphere 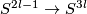 , Hudson's examples were the first examples of embeddings in codimension greater than 2 not isotopic to the standard embedding. (Hudson's construction [Hudson1963] was not as explicit as the one below).
, Hudson's examples were the first examples of embeddings in codimension greater than 2 not isotopic to the standard embedding. (Hudson's construction [Hudson1963] was not as explicit as the one below).
For 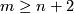 define the
define the 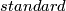
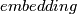
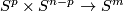 as the composition
as the composition 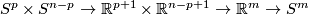 of standard embeddings.
of standard embeddings.
3.1 Hudson tori 1
In this subsection, we recall for 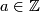 and
and  . Hudson's construction of embedings
. Hudson's construction of embedings
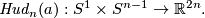
Take the standard embeddings 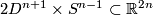 (where
(where  means homothety with coefficient 2) and
means homothety with coefficient 2) and
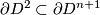 .
Fix a point
.
Fix a point 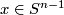 .
The Hudson torus
.
The Hudson torus 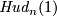 is the embedded connected sum of
is the embedded connected sum of
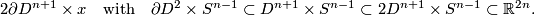
(Unlike the connected sum mentioned in embedded conntected sum this is a `linked' connected sum, i.e. connected sum of two embeddings whose images are not contained in disjoint cubes.)
For 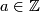 instead of an embedded
instead of an embedded  -sphere
-sphere 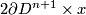 we can take
we can take  copies
copies 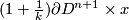 (
(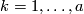 ) of
) of  -sphere outside
-sphere outside 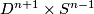 `parallel' to
`parallel' to
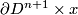 .
Then we join these spheres by tubes so that the homotopy class of the resulting embedding
.
Then we join these spheres by tubes so that the homotopy class of the resulting embedding
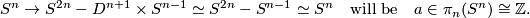
Let  be the connected sum of this embedding with the above standard
embedding
be the connected sum of this embedding with the above standard
embedding 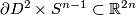 .
.
Clearly, 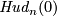 is isotopic to the standard embedding.
is isotopic to the standard embedding.
Proposition 3.1.
For  odd
odd  is isotopic to
is isotopic to 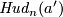 if and only
if
if and only
if 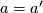 .
.
For 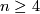 even
even  is isotopic to
is isotopic to 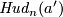 if and only if
if and only if
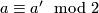 .
.
In particular, 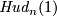 is not isotopic to
is not isotopic to 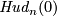 for each
for each  (this was the original motivation for Hudson).
(this was the original motivation for Hudson).
Proposition 3.1 follows by Remark 5.e and, for  even, by Theorem 4, both results from classification just below the stable range.
even, by Theorem 4, both results from classification just below the stable range.
It would be interesting to find an explicit construction of an isotopy between
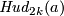 and
and 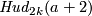 (cf. [Vrabec1977], \S6) and to prove the analogue of
Proposition 3.1 for
(cf. [Vrabec1977], \S6) and to prove the analogue of
Proposition 3.1 for  .
.
3.2 Hudson tori 2
In this subsection we give, for 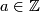 and
and  another construction of embeddings
another construction of embeddings
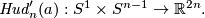
Define a map 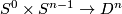 to be the constant
to be the constant 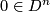 on one
component
on one
component 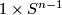 and the standard embedding
and the standard embedding
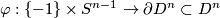 on the other component.
This map gives an
on the other component.
This map gives an 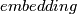
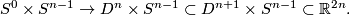
(See Figure 2.2 of [Skopenkov2006].)
Each disk 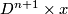 intersects the image of this embedding at two
points lying in
intersects the image of this embedding at two
points lying in 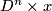 .
Extend this embedding
.
Extend this embedding 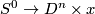 for each
for each 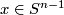 to an
embedding
to an
embedding 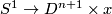 .
(See Figure 2.3 of [Skopenkov2006].)
Thus we obtain the Hudson torus
.
(See Figure 2.3 of [Skopenkov2006].)
Thus we obtain the Hudson torus
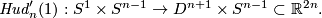
The embedding 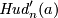 is obtained in the same way starting from a map
is obtained in the same way starting from a map
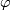 of degree
of degree  .
.
The same proposition as above holds with 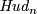 replaced to
replaced to 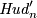 .
.
3.3 Remarks
We have  is PL isotopic to
is PL isotopic to 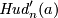 [Skopenkov2006a].
It would be interesting to prove the smooth analogue of this result.
[Skopenkov2006a].
It would be interesting to prove the smooth analogue of this result.
For  these construction give what we call the
these construction give what we call the 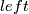 Hudson torus.
The
Hudson torus.
The 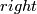 Hudson torus is constructed analogously and is the
composition of the left Hudson torus and the exchanging factors
autodiffeomorphism of
Hudson torus is constructed analogously and is the
composition of the left Hudson torus and the exchanging factors
autodiffeomorphism of 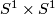 .
.
Analogously one constructs the Hudson torus 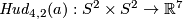 for
for 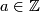 or, more generally,
or, more generally, 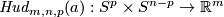 for
for 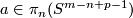 and
and 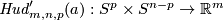 for
for 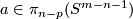 .
.
3.4 An action of the first homology group on embeddings
In this subsection, for 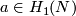 and for orientable
and for orientable  with
with  , we construct an embedding
, we construct an embedding 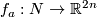 from an embedding
from an embedding 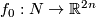 .
.
For 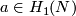 , represent
, represent  by an embedding
by an embedding 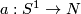 . Since any orientable bundle over
. Since any orientable bundle over  is trivial,
is trivial, 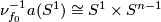 . Identify
. Identify 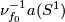 with
with 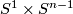 . It remains to make an embedded surgery of
. It remains to make an embedded surgery of
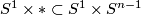 to obtain an
to obtain an  -sphere
-sphere 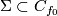 , and then we set
, and then we set 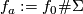 .
.
Take a vector field on 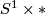 normal to
normal to 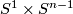 . Extend
. Extend 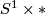 along this vector field to a smooth map
along this vector field to a smooth map
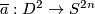 . Since
. Since 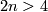 and
and 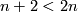 , by general position we may assume that
, by general position we may assume that 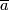 is an embedding and
is an embedding and 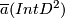 misses
misses 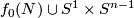 . Since
. Since 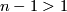 , we have
, we have 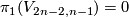 .
Hence the standard framing of
.
Hence the standard framing of 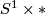 in
in 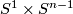 extends to an
extends to an  -framing on
-framing on 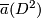 in
in  .
Thus
.
Thus  extends to an embedding
extends to an embedding

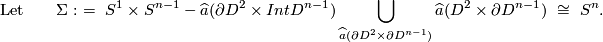
This construction generalizes the construction of  (from
(from 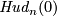 ).
).
Clearly, 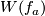 is
is  or
or  . Thus unless
. Thus unless  and CAT=DIFF
and CAT=DIFF
- all isotopy classes of embedings
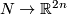 can be obtained (from a certain given embedding
can be obtained (from a certain given embedding  ) by the above construction;
) by the above construction;
- the above construction defines an action
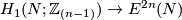 .
.
4 The Whitney invariant (for either n odd or N orientable)
Fix orientations on  and, if
and, if  is even, on
is even, on  . Fix an embedding
. Fix an embedding 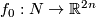 . For an embedding
. For an embedding 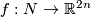 the restrictions of
the restrictions of  and
and  to
to  are regular homotopic [Hirsch1959]. Since
are regular homotopic [Hirsch1959]. Since  has an
has an  -dimensional spine, it follows that these restrictions are isotopic, cf. [Haefliger&Hirsch1963], 3.1.b, [Takase2006], Lemma 2.2. So we can make an isotopy of
-dimensional spine, it follows that these restrictions are isotopic, cf. [Haefliger&Hirsch1963], 3.1.b, [Takase2006], Lemma 2.2. So we can make an isotopy of  and assume that
and assume that 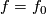 on
on  . Take a general position homotopy
. Take a general position homotopy 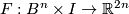 relative to
relative to
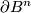 between the restrictions of
between the restrictions of  and
and  to
to  . Then
. Then 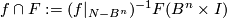 (i.e. `the intersection of this homotopy with
(i.e. `the intersection of this homotopy with 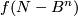 ') is a 1-manifold (possibly non-compact) without boundary. Define
') is a 1-manifold (possibly non-compact) without boundary. Define 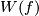 to be the homology class of the closure of this 1-manifold:
to be the homology class of the closure of this 1-manifold:
![\displaystyle W(f):=[Cl(f\cap F)]\in H_1(N_0,\partial N_0;\Zz_{(n)})\cong H_1(N;\Zz_{(n)}).](/images/math/2/b/b/2bbc331d0f1495918467d3ff52161652.png)
The orientation on  is defined for
is defined for  orientable as follows. (This orientation is defined for each
orientable as follows. (This orientation is defined for each  but used only for odd
but used only for odd  .) For each point
.) For each point 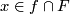 take a vector at
take a vector at  tangent to
tangent to  . Complete this vector to a positive base tangent to
. Complete this vector to a positive base tangent to  . Since
. Since 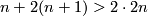 , by general position there is a unique point
, by general position there is a unique point 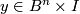 such that
such that 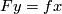 . The tangent vector at
. The tangent vector at  thus gives a tangent vector at
thus gives a tangent vector at  to
to 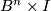 . Complete this vector to a positive base tangent to
. Complete this vector to a positive base tangent to 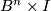 , where the orientation on
, where the orientation on  comes from
comes from  . The union of the images of the constructed two bases is a base at
. The union of the images of the constructed two bases is a base at 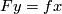 of
of  . If this base is positive, then call the initial vector of
. If this base is positive, then call the initial vector of  positive. Since a change of the orientation on
positive. Since a change of the orientation on  forces a change of the orientation of the latter base of
forces a change of the orientation of the latter base of  , it follows that this condition indeed defines an orientation on
, it follows that this condition indeed defines an orientation on  .
.
Remark 4.1.
- The Whitney invariant is well-defined, i.e. independent of the choice of
 and of the isotopy making
and of the isotopy making 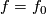 outside
outside  . This is so because the above definition is clearly equivalent to the following:
. This is so because the above definition is clearly equivalent to the following: 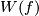 is the homology class of the algebraic sum of the top-dimensional simplices of the self-intersection set
is the homology class of the algebraic sum of the top-dimensional simplices of the self-intersection set 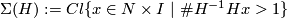 of a general position homotopy
of a general position homotopy  between
between  and
and  . (For details and definition of the signs of the simplices see [Hudson1969], \S12, [Vrabec1977], p. 145, [Skopenkov2006], \S2, [Skopenkov2010].) It is for being well-defined that we need
. (For details and definition of the signs of the simplices see [Hudson1969], \S12, [Vrabec1977], p. 145, [Skopenkov2006], \S2, [Skopenkov2010].) It is for being well-defined that we need  -coefficients when
-coefficients when  is even.
is even.
- Clearly,
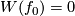 . The definition of
. The definition of  depends on the choice of
depends on the choice of  , but we write
, but we write  not
not 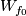 for brevity.
for brevity.
- Since a change of the orientation on
 forces a change of the orientation on
forces a change of the orientation on  , the class
, the class 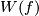 is independent of the choice of the orientation on
is independent of the choice of the orientation on  . For the reflection
. For the reflection 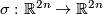 with respect to a hyperplane we have
with respect to a hyperplane we have 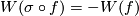 (because we may assume that
(because we may assume that 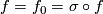 on
on  and because a change of the orientation of
and because a change of the orientation of  forces a change of the orientation of
forces a change of the orientation of  ).
).
- The above definition makes sense for each
 , not only for
, not only for  .
.
- Clearly,
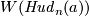 is
is  or
or  for
for  for the Hudson tori.
for the Hudson tori.
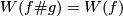 for each embeddings
for each embeddings 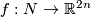 and
and 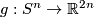 .
.
5 A generalization to highly-connected manifolds
Examples are the above Hudson tori 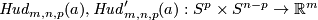 . See also [Milgram&Rees1971].
. See also [Milgram&Rees1971].
5.1 Classification
Theorem 5.1. Let  be a closed orientable homologically
be a closed orientable homologically  -connected
-connected  -manifold,
-manifold, 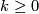 . Then the Whitney invariant
. Then the Whitney invariant
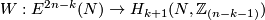
is a bijection, provided 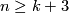 or
or 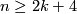 in the PL or DIFF categories, respectively.
in the PL or DIFF categories, respectively.
Theorem 5.1 was proved in [Haefliger&Hirsch1963], [Hudson1969], \S11, [Boechat&Haefliger1970], [Boechat1971], [Vrabec1977] 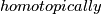
 -connected manifolds. The proof works for
-connected manifolds. The proof works for 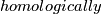
 -connected manifolds.
-connected manifolds.
E.g. by Theorem 5.1 we obtain that the Whitney invariant 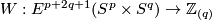 is bijective for
is bijective for 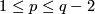 .
It is in fact a group isomorphism; the generator is the Hudson torus.
.
It is in fact a group isomorphism; the generator is the Hudson torus.
The PL case of Theorem 5.1 gives nothing but the Unknotting Spheres Theorem for 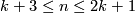 .
.
Analogously to Theorem 5.1 it may be proved that
- if
 is a closed connected non-orientable
is a closed connected non-orientable  -manifold, then
-manifold, then
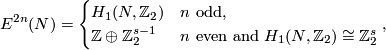
provided  or
or 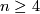 in the PL or DIFF categories, respectively.
in the PL or DIFF categories, respectively.
This is proved in [Haefliger1962b], [Weber1967], [Bausum1975], [Vrabec1977] (a minor miscalculation being corrected only in [Vrabec1977]).
Because of the existence of knots the analogues of Theorem 5.1 for 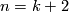 in the PL case, and for
in the PL case, and for 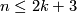 in the smooth case are false. So for the smooth category and
in the smooth case are false. So for the smooth category and 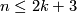 a classification is much harder: for 40 years the
a classification is much harder: for 40 years the 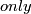 known concrete complete classification results were for spheres. The following result was obtained using the Kreck modification of surgery theory.
known concrete complete classification results were for spheres. The following result was obtained using the Kreck modification of surgery theory.
Theorem 5.2. [Skopenkov2006] Let  be a closed homologically
be a closed homologically 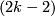 -connected
-connected  -manifold. Then the Whitney invariant
-manifold. Then the Whitney invariant 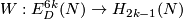 is surjective and for each
is surjective and for each 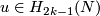 there is a 1--1 correspondence
there is a 1--1 correspondence
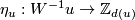 , where
, where 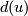 is the divisibility of the projection of
is the divisibility of the projection of  to the free part of
to the free part of 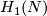 .
.
Recall that the divisibility of zero is zero and the divisibility of 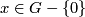 is
is 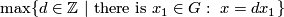 . E.g. by Theorem 5.2 we obtain that
. E.g. by Theorem 5.2 we obtain that
- the Whitney invariant
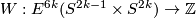 is surjective and for each
is surjective and for each 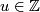 there is a 1--1 correspondence
there is a 1--1 correspondence 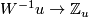 .
.
5.2 The Whitney invariant
6 References
- [Bausum1975] D. R. Bausum, Embeddings and immersions of manifolds in Euclidean space, Trans. Amer. Math. Soc. 213 (1975), 263–303. MR0474330 (57 #13976) Zbl 0323.57017
- [Boechat&Haefliger1970] J. Boéchat and A. Haefliger, Plongements différentiables des variétés orientées de dimension
 dans
dans 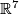 , (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
, (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
- [Boechat1971] J. Boéchat, Plongements de variétées différentiables orientées de dimension
 dans
dans 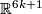 , Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
, Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
- [Haefliger&Hirsch1963] A. Haefliger and M. W. Hirsch, On the existence and classification of differentiable embeddings, Topology 2 (1963), 129–135. see also MR0149494 (26 #6981) Zbl 0113.38607
- [Haefliger1962b] A. Haefliger, Plongements de variétés dans le domain stable, Séminaire Bourbaki, 245 (1962).
- [Hirsch1959] M. W. Hirsch, Immersions of manifolds, Trans. Amer. Math. Soc. 93 (1959), 242–276. MR0119214 (22 #9980) Zbl 0118.18603
- [Hudson1963] J. F. P. Hudson, Knotted tori, Topology 2 (1963), 11–22. MR0146829 (26 #4349) Zbl 0151.32503
- [Hudson1969] J. F. P. Hudson, Piecewise linear topology, W. A. Benjamin, Inc., New York-Amsterdam, 1969. MR0248844 (40 #2094) Zbl 0189.54507
- [Milgram&Rees1971] R. Milgram and E. Rees, On the normal bundle to an embedding., Topology 10 (1971), 299-308. MR0290391 (44 #7572) Zbl 0207.22302
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2006a] A. Skopenkov, Classification of embeddings below the metastable dimension. Available at the arXiv:0607422.
- [Skopenkov2010] A. Skopenkov, Embeddings of k-connected n-manifolds into
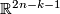 , Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
, Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
- [Takase2006] M. Takase, Homology 3-spheres in codimension three, Internat. J. Math. 17 (2006), no.8, 869–885.
arxiv:math/0506464 MR2261638 (2007g:57049) Zbl 1113.57013
- [Vrabec1977] J. Vrabec, Knotting a
 -connected closed
-connected closed 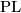
 -manifold in
-manifold in 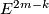 , Trans. Amer. Math. Soc. 233 (1977), 137–165. MR0645405 (58 #31097) Zbl 386.57013
, Trans. Amer. Math. Soc. 233 (1977), 137–165. MR0645405 (58 #31097) Zbl 386.57013
- [Weber1967] C. Weber, Plongements de polyedres dans le domaine metastable, Comment. Math. Helv. 42 (1967), 1-27. MR0238330 (38 #6606) Zbl 0152.22402
|
This page has not been refereed. The information given here might be incomplete or provisional. |
 , then there is just one isotopy class of embedding
, then there is just one isotopy class of embedding 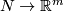 if
if 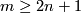 . In this page we summarise the situation for
. In this page we summarise the situation for 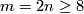 , and give references to the case
, and give references to the case 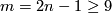 .
.
For notation and conventions see high codimension embeddings.
2 Classification
Classification Theorem 2.1.
Let  be a closed connected
be a closed connected  -manifold. The Whitney invariant
-manifold. The Whitney invariant
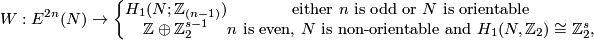
is bijective if either 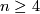 or
or  and CAT=PL [Haefliger&Hirsch1963], [Bausum1975], [Vrabec1977], cf. [Hudson1969]
and CAT=PL [Haefliger&Hirsch1963], [Bausum1975], [Vrabec1977], cf. [Hudson1969]
The Whitney invariant is defined below.
The classification of smooth embeddings of 3-manifolds in 6-space is more complicated. For analogous classification of 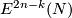 see Embeddings of highly-connected manifolds. Some estimations of
see Embeddings of highly-connected manifolds. Some estimations of 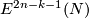 for a closed
for a closed  -connected
-connected  -manifold
-manifold  and
and 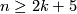 (including
(including  ) are presented in [Skopenkov2010]. See also Embeddings of 4-manifolds in 7-space.
) are presented in [Skopenkov2010]. See also Embeddings of 4-manifolds in 7-space.
3 Examples
Together with the Haefliger knotted sphere 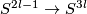 , Hudson's examples were the first examples of embeddings in codimension greater than 2 not isotopic to the standard embedding. (Hudson's construction [Hudson1963] was not as explicit as the one below).
, Hudson's examples were the first examples of embeddings in codimension greater than 2 not isotopic to the standard embedding. (Hudson's construction [Hudson1963] was not as explicit as the one below).
For 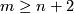 define the
define the 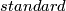
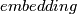
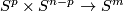 as the composition
as the composition 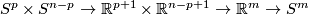 of standard embeddings.
of standard embeddings.
3.1 Hudson tori 1
In this subsection, we recall for 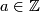 and
and  . Hudson's construction of embedings
. Hudson's construction of embedings
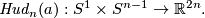
Take the standard embeddings 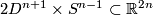 (where
(where  means homothety with coefficient 2) and
means homothety with coefficient 2) and
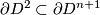 .
Fix a point
.
Fix a point 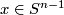 .
The Hudson torus
.
The Hudson torus 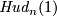 is the embedded connected sum of
is the embedded connected sum of
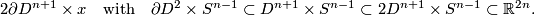
(Unlike the connected sum mentioned in embedded conntected sum this is a `linked' connected sum, i.e. connected sum of two embeddings whose images are not contained in disjoint cubes.)
For 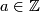 instead of an embedded
instead of an embedded  -sphere
-sphere 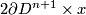 we can take
we can take  copies
copies 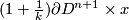 (
(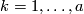 ) of
) of  -sphere outside
-sphere outside 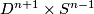 `parallel' to
`parallel' to
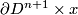 .
Then we join these spheres by tubes so that the homotopy class of the resulting embedding
.
Then we join these spheres by tubes so that the homotopy class of the resulting embedding
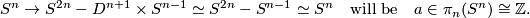
Let  be the connected sum of this embedding with the above standard
embedding
be the connected sum of this embedding with the above standard
embedding 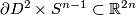 .
.
Clearly, 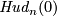 is isotopic to the standard embedding.
is isotopic to the standard embedding.
Proposition 3.1.
For  odd
odd  is isotopic to
is isotopic to 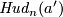 if and only
if
if and only
if 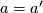 .
.
For 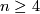 even
even  is isotopic to
is isotopic to 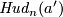 if and only if
if and only if
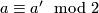 .
.
In particular, 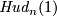 is not isotopic to
is not isotopic to 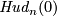 for each
for each  (this was the original motivation for Hudson).
(this was the original motivation for Hudson).
Proposition 3.1 follows by Remark 5.e and, for  even, by Theorem 4, both results from classification just below the stable range.
even, by Theorem 4, both results from classification just below the stable range.
It would be interesting to find an explicit construction of an isotopy between
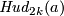 and
and 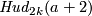 (cf. [Vrabec1977], \S6) and to prove the analogue of
Proposition 3.1 for
(cf. [Vrabec1977], \S6) and to prove the analogue of
Proposition 3.1 for  .
.
3.2 Hudson tori 2
In this subsection we give, for 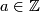 and
and  another construction of embeddings
another construction of embeddings
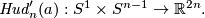
Define a map 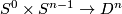 to be the constant
to be the constant 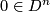 on one
component
on one
component 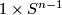 and the standard embedding
and the standard embedding
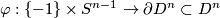 on the other component.
This map gives an
on the other component.
This map gives an 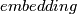
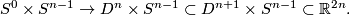
(See Figure 2.2 of [Skopenkov2006].)
Each disk 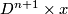 intersects the image of this embedding at two
points lying in
intersects the image of this embedding at two
points lying in 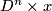 .
Extend this embedding
.
Extend this embedding 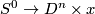 for each
for each 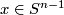 to an
embedding
to an
embedding 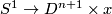 .
(See Figure 2.3 of [Skopenkov2006].)
Thus we obtain the Hudson torus
.
(See Figure 2.3 of [Skopenkov2006].)
Thus we obtain the Hudson torus
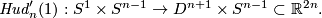
The embedding 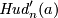 is obtained in the same way starting from a map
is obtained in the same way starting from a map
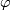 of degree
of degree  .
.
The same proposition as above holds with 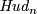 replaced to
replaced to 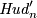 .
.
3.3 Remarks
We have  is PL isotopic to
is PL isotopic to 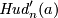 [Skopenkov2006a].
It would be interesting to prove the smooth analogue of this result.
[Skopenkov2006a].
It would be interesting to prove the smooth analogue of this result.
For  these construction give what we call the
these construction give what we call the 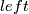 Hudson torus.
The
Hudson torus.
The 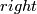 Hudson torus is constructed analogously and is the
composition of the left Hudson torus and the exchanging factors
autodiffeomorphism of
Hudson torus is constructed analogously and is the
composition of the left Hudson torus and the exchanging factors
autodiffeomorphism of 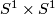 .
.
Analogously one constructs the Hudson torus 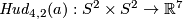 for
for 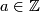 or, more generally,
or, more generally, 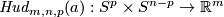 for
for 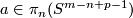 and
and 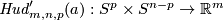 for
for 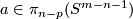 .
.
3.4 An action of the first homology group on embeddings
In this subsection, for 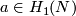 and for orientable
and for orientable  with
with  , we construct an embedding
, we construct an embedding 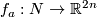 from an embedding
from an embedding 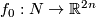 .
.
For 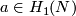 , represent
, represent  by an embedding
by an embedding 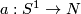 . Since any orientable bundle over
. Since any orientable bundle over  is trivial,
is trivial, 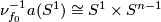 . Identify
. Identify 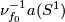 with
with 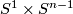 . It remains to make an embedded surgery of
. It remains to make an embedded surgery of
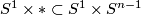 to obtain an
to obtain an  -sphere
-sphere 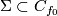 , and then we set
, and then we set 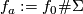 .
.
Take a vector field on 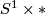 normal to
normal to 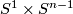 . Extend
. Extend 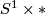 along this vector field to a smooth map
along this vector field to a smooth map
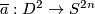 . Since
. Since 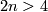 and
and 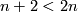 , by general position we may assume that
, by general position we may assume that 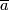 is an embedding and
is an embedding and 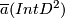 misses
misses 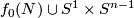 . Since
. Since 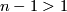 , we have
, we have 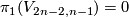 .
Hence the standard framing of
.
Hence the standard framing of 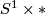 in
in 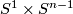 extends to an
extends to an  -framing on
-framing on  in
in  .
Thus
.
Thus  extends to an embedding
extends to an embedding

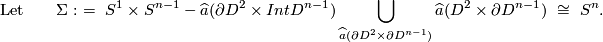
This construction generalizes the construction of  (from
(from 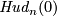 ).
).
Clearly, 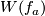 is
is  or
or  . Thus unless
. Thus unless  and CAT=DIFF
and CAT=DIFF
- all isotopy classes of embedings
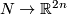 can be obtained (from a certain given embedding
can be obtained (from a certain given embedding  ) by the above construction;
) by the above construction;
- the above construction defines an action
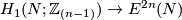 .
.
4 The Whitney invariant (for either n odd or N orientable)
Fix orientations on  and, if
and, if  is even, on
is even, on  . Fix an embedding
. Fix an embedding 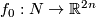 . For an embedding
. For an embedding 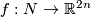 the restrictions of
the restrictions of  and
and  to
to  are regular homotopic [Hirsch1959]. Since
are regular homotopic [Hirsch1959]. Since  has an
has an  -dimensional spine, it follows that these restrictions are isotopic, cf. [Haefliger&Hirsch1963], 3.1.b, [Takase2006], Lemma 2.2. So we can make an isotopy of
-dimensional spine, it follows that these restrictions are isotopic, cf. [Haefliger&Hirsch1963], 3.1.b, [Takase2006], Lemma 2.2. So we can make an isotopy of  and assume that
and assume that 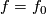 on
on  . Take a general position homotopy
. Take a general position homotopy 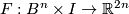 relative to
relative to
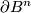 between the restrictions of
between the restrictions of  and
and  to
to  . Then
. Then 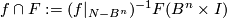 (i.e. `the intersection of this homotopy with
(i.e. `the intersection of this homotopy with 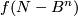 ') is a 1-manifold (possibly non-compact) without boundary. Define
') is a 1-manifold (possibly non-compact) without boundary. Define 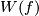 to be the homology class of the closure of this 1-manifold:
to be the homology class of the closure of this 1-manifold:
![\displaystyle W(f):=[Cl(f\cap F)]\in H_1(N_0,\partial N_0;\Zz_{(n)})\cong H_1(N;\Zz_{(n)}).](/images/math/2/b/b/2bbc331d0f1495918467d3ff52161652.png)
The orientation on  is defined for
is defined for  orientable as follows. (This orientation is defined for each
orientable as follows. (This orientation is defined for each  but used only for odd
but used only for odd  .) For each point
.) For each point 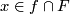 take a vector at
take a vector at  tangent to
tangent to  . Complete this vector to a positive base tangent to
. Complete this vector to a positive base tangent to  . Since
. Since 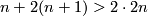 , by general position there is a unique point
, by general position there is a unique point 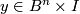 such that
such that 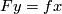 . The tangent vector at
. The tangent vector at  thus gives a tangent vector at
thus gives a tangent vector at  to
to 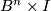 . Complete this vector to a positive base tangent to
. Complete this vector to a positive base tangent to 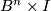 , where the orientation on
, where the orientation on  comes from
comes from  . The union of the images of the constructed two bases is a base at
. The union of the images of the constructed two bases is a base at 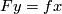 of
of  . If this base is positive, then call the initial vector of
. If this base is positive, then call the initial vector of  positive. Since a change of the orientation on
positive. Since a change of the orientation on  forces a change of the orientation of the latter base of
forces a change of the orientation of the latter base of  , it follows that this condition indeed defines an orientation on
, it follows that this condition indeed defines an orientation on  .
.
Remark 4.1.
- The Whitney invariant is well-defined, i.e. independent of the choice of
 and of the isotopy making
and of the isotopy making 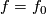 outside
outside  . This is so because the above definition is clearly equivalent to the following:
. This is so because the above definition is clearly equivalent to the following:  is the homology class of the algebraic sum of the top-dimensional simplices of the self-intersection set
is the homology class of the algebraic sum of the top-dimensional simplices of the self-intersection set 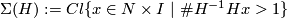 of a general position homotopy
of a general position homotopy  between
between  and
and  . (For details and definition of the signs of the simplices see [Hudson1969], \S12, [Vrabec1977], p. 145, [Skopenkov2006], \S2, [Skopenkov2010].) It is for being well-defined that we need
. (For details and definition of the signs of the simplices see [Hudson1969], \S12, [Vrabec1977], p. 145, [Skopenkov2006], \S2, [Skopenkov2010].) It is for being well-defined that we need  -coefficients when
-coefficients when  is even.
is even.
- Clearly,
 . The definition of
. The definition of  depends on the choice of
depends on the choice of  , but we write
, but we write  not
not  for brevity.
for brevity.
- Since a change of the orientation on
 forces a change of the orientation on
forces a change of the orientation on  , the class
, the class 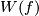 is independent of the choice of the orientation on
is independent of the choice of the orientation on  . For the reflection
. For the reflection 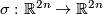 with respect to a hyperplane we have
with respect to a hyperplane we have 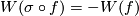 (because we may assume that
(because we may assume that 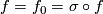 on
on  and because a change of the orientation of
and because a change of the orientation of  forces a change of the orientation of
forces a change of the orientation of  ).
).
- The above definition makes sense for each
 , not only for
, not only for  .
.
- Clearly,
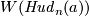 is
is  or
or  for
for  for the Hudson tori.
for the Hudson tori.
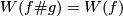 for each embeddings
for each embeddings 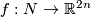 and
and 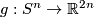 .
.
5 A generalization to highly-connected manifolds
Examples are the above Hudson tori 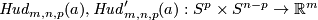 . See also [Milgram&Rees1971].
. See also [Milgram&Rees1971].
5.1 Classification
Theorem 5.1. Let  be a closed orientable homologically
be a closed orientable homologically  -connected
-connected  -manifold,
-manifold, 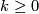 . Then the Whitney invariant
. Then the Whitney invariant
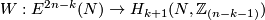
is a bijection, provided 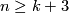 or
or 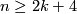 in the PL or DIFF categories, respectively.
in the PL or DIFF categories, respectively.
Theorem 5.1 was proved in [Haefliger&Hirsch1963], [Hudson1969], \S11, [Boechat&Haefliger1970], [Boechat1971], [Vrabec1977] 
 -connected manifolds. The proof works for
-connected manifolds. The proof works for 
 -connected manifolds.
-connected manifolds.
E.g. by Theorem 5.1 we obtain that the Whitney invariant 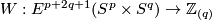 is bijective for
is bijective for 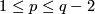 .
It is in fact a group isomorphism; the generator is the Hudson torus.
.
It is in fact a group isomorphism; the generator is the Hudson torus.
The PL case of Theorem 5.1 gives nothing but the Unknotting Spheres Theorem for 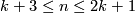 .
.
Analogously to Theorem 5.1 it may be proved that
- if
 is a closed connected non-orientable
is a closed connected non-orientable  -manifold, then
-manifold, then
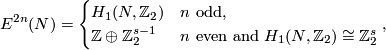
provided  or
or 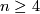 in the PL or DIFF categories, respectively.
in the PL or DIFF categories, respectively.
This is proved in [Haefliger1962b], [Weber1967], [Bausum1975], [Vrabec1977] (a minor miscalculation being corrected only in [Vrabec1977]).
Because of the existence of knots the analogues of Theorem 5.1 for 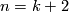 in the PL case, and for
in the PL case, and for 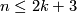 in the smooth case are false. So for the smooth category and
in the smooth case are false. So for the smooth category and 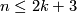 a classification is much harder: for 40 years the
a classification is much harder: for 40 years the  known concrete complete classification results were for spheres. The following result was obtained using the Kreck modification of surgery theory.
known concrete complete classification results were for spheres. The following result was obtained using the Kreck modification of surgery theory.
Theorem 5.2. [Skopenkov2006] Let  be a closed homologically
be a closed homologically 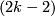 -connected
-connected  -manifold. Then the Whitney invariant
-manifold. Then the Whitney invariant 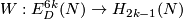 is surjective and for each
is surjective and for each 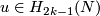 there is a 1--1 correspondence
there is a 1--1 correspondence
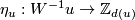 , where
, where 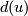 is the divisibility of the projection of
is the divisibility of the projection of  to the free part of
to the free part of 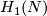 .
.
Recall that the divisibility of zero is zero and the divisibility of 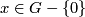 is
is 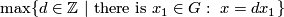 . E.g. by Theorem 5.2 we obtain that
. E.g. by Theorem 5.2 we obtain that
- the Whitney invariant
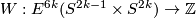 is surjective and for each
is surjective and for each 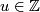 there is a 1--1 correspondence
there is a 1--1 correspondence 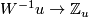 .
.
5.2 The Whitney invariant
6 References
- [Bausum1975] D. R. Bausum, Embeddings and immersions of manifolds in Euclidean space, Trans. Amer. Math. Soc. 213 (1975), 263–303. MR0474330 (57 #13976) Zbl 0323.57017
- [Boechat&Haefliger1970] J. Boéchat and A. Haefliger, Plongements différentiables des variétés orientées de dimension
 dans
dans 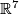 , (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
, (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
- [Boechat1971] J. Boéchat, Plongements de variétées différentiables orientées de dimension
 dans
dans 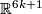 , Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
, Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
- [Haefliger&Hirsch1963] A. Haefliger and M. W. Hirsch, On the existence and classification of differentiable embeddings, Topology 2 (1963), 129–135. see also MR0149494 (26 #6981) Zbl 0113.38607
- [Haefliger1962b] A. Haefliger, Plongements de variétés dans le domain stable, Séminaire Bourbaki, 245 (1962).
- [Hirsch1959] M. W. Hirsch, Immersions of manifolds, Trans. Amer. Math. Soc. 93 (1959), 242–276. MR0119214 (22 #9980) Zbl 0118.18603
- [Hudson1963] J. F. P. Hudson, Knotted tori, Topology 2 (1963), 11–22. MR0146829 (26 #4349) Zbl 0151.32503
- [Hudson1969] J. F. P. Hudson, Piecewise linear topology, W. A. Benjamin, Inc., New York-Amsterdam, 1969. MR0248844 (40 #2094) Zbl 0189.54507
- [Milgram&Rees1971] R. Milgram and E. Rees, On the normal bundle to an embedding., Topology 10 (1971), 299-308. MR0290391 (44 #7572) Zbl 0207.22302
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2006a] A. Skopenkov, Classification of embeddings below the metastable dimension. Available at the arXiv:0607422.
- [Skopenkov2010] A. Skopenkov, Embeddings of k-connected n-manifolds into
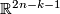 , Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
, Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
- [Takase2006] M. Takase, Homology 3-spheres in codimension three, Internat. J. Math. 17 (2006), no.8, 869–885.
arxiv:math/0506464 MR2261638 (2007g:57049) Zbl 1113.57013
- [Vrabec1977] J. Vrabec, Knotting a
 -connected closed
-connected closed 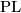
 -manifold in
-manifold in 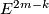 , Trans. Amer. Math. Soc. 233 (1977), 137–165. MR0645405 (58 #31097) Zbl 386.57013
, Trans. Amer. Math. Soc. 233 (1977), 137–165. MR0645405 (58 #31097) Zbl 386.57013
- [Weber1967] C. Weber, Plongements de polyedres dans le domaine metastable, Comment. Math. Helv. 42 (1967), 1-27. MR0238330 (38 #6606) Zbl 0152.22402
|
This page has not been refereed. The information given here might be incomplete or provisional. |