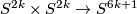4-manifolds in 7-space
|
The user responsible for this page is Askopenkov. No other user may edit this page at present. |
Contents |
1 Introduction
Most of this page is intended not only for specialists in embeddings, but also for mathematician from other areas who want to apply or to learn the theory of embeddings.
Basic results on embeddings of closed connected 4-manifolds in 7-space are particular cases of results on
embeddings of  -manifolds in
-manifolds in  -space which are discussed in [Skopenkov2016e], [Skopenkov2006,
-space which are discussed in [Skopenkov2016e], [Skopenkov2006,  2.4 `The Whitney invariant'].
In this page we concentrate on more advanced classification results peculiar for
2.4 `The Whitney invariant'].
In this page we concentrate on more advanced classification results peculiar for 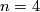 .
.
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3].
Unless specified otherwise, we work in the smooth category.
For the definition of the
embedded connected sum
3].
Unless specified otherwise, we work in the smooth category.
For the definition of the
embedded connected sum  of embeddings of closed connected 4-manifolds
of embeddings of closed connected 4-manifolds  in 7-space and for the corresponding action of the group
in 7-space and for the corresponding action of the group 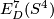 on the set
on the set 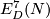 , see e.g. [Skopenkov2016c,
, see e.g. [Skopenkov2016c,  4].
4].
Remark 1.1 (PL and piecewise smooth embeddings). Any smooth manifold has a unique (up to PL homeomorphism) PL structure compatible with the given smooth structure [Milnor&Stasheff1974, Complement, Theorems 10.5 and 10.6]. Since also any PL 4-manifold admits a unique smooth structure [Mandelbaum1980,  1.2], we may consider a smooth 4-manifold as a PL 4-manifold.
1.2], we may consider a smooth 4-manifold as a PL 4-manifold.
A map of a smooth manifold is 'piecewise smooth (PS)' if it is smooth on every simplex of some triangulation of the manifold. Clearly, every smooth or PL map is PS.
For a smooth manifold  let
let 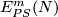 be the set of PS embeddings
be the set of PS embeddings 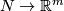 up to PS isotopy.
The forgetful map
up to PS isotopy.
The forgetful map 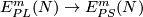 is 1-1 [Haefliger1967, 2.4].
So a description of
is 1-1 [Haefliger1967, 2.4].
So a description of 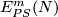 is equivalent to a description of
is equivalent to a description of 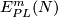 .
.
2 Examples of knotted tori
The Hudson tori 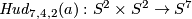 and
and 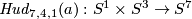 are defined for an integer
are defined for an integer  in Remark 3.5.d of [Skopenkov2016e] or in [Skopenkov2006, Example 2.10].
in Remark 3.5.d of [Skopenkov2016e] or in [Skopenkov2006, Example 2.10].
Define 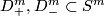 by the equations
by the equations 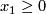 and
and 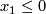 , respectively.
, respectively.
Example 2.1 (Spinning construction).
For an embedding 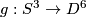 denote by
denote by 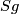 the embedding
the embedding
Tex syntax error
The restriction of 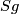 to
to 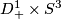 is isotopic to (the restriction to
is isotopic to (the restriction to 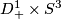 of) the standard embedding.
We conjecture that if
of) the standard embedding.
We conjecture that if 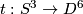 is the Haefliger trefoil knot [Skopenkov2016t, Example 2.1], then
is the Haefliger trefoil knot [Skopenkov2016t, Example 2.1], then 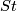 is not smoothly isotopic to the connected sum of the standard embedding and any embedding
is not smoothly isotopic to the connected sum of the standard embedding and any embedding 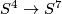 .
.
The following Examples 2.2 and 2.3 appear in [Skopenkov2002,  6], [Skopenkov2006,
6], [Skopenkov2006,  6] but could be known earlier.
6] but could be known earlier.
Example 2.2.
Two embeddings 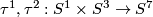 are defined as compositions
are defined as compositions
Tex syntax error
where 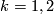 and maps
and maps 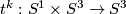 are defined below.
We shall see that
are defined below.
We shall see that 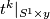 is an embedding for any
is an embedding for any 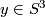 and
and 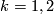 , hence
, hence 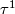 and
and 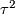 are embeddings.
are embeddings.
Define 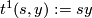 , where
, where  is identified with the set of unit length quaternions and
is identified with the set of unit length quaternions and 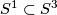 with the set of unit length complex numbers.
with the set of unit length complex numbers.
Define 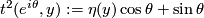 , where
, where 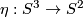 is the Hopf fibration and
is the Hopf fibration and  is identified with the 2-sphere formed by unit length quaternions of the form
is identified with the 2-sphere formed by unit length quaternions of the form 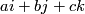 .
.
It would be interesting to know if 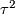 is PS or smoothly isotopic to the Hudson torus
is PS or smoothly isotopic to the Hudson torus 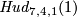 .
.
Example 2.2 can be generalized as follows.
Example 2.3. Define a map 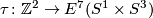 .
Take a smooth map
.
Take a smooth map 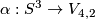 .
Assuming that
.
Assuming that  , we have
, we have 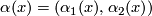 .
Define the adjunction map
.
Define the adjunction map 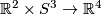 by
by 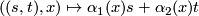 .
(Assuming that
.
(Assuming that 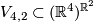 , this map is obtained from
, this map is obtained from  by the exponential law.)
Denote by
by the exponential law.)
Denote by 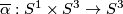 the restriction of the adjunction map.
We define the embedding
the restriction of the adjunction map.
We define the embedding 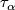 to be the composition
to be the composition
Tex syntax error
We define the map  by
by ![\tau(l, b):=[\tau_{\alpha}]](/images/math/5/7/e/57e4042672c04f982e2359a88c4e92f7.png) , where
, where 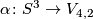 represents
represents
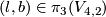 (for the standard identification
(for the standard identification 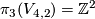 ).
).
Clearly, ![[\tau^1]=\tau(1,0)](/images/math/d/6/2/d62ddb518a51ddc58f1f76a34106c9d2.png) and
and ![[\tau^2]=\tau(0,1)](/images/math/7/7/9/7793380c62f9cc8e650ebb0791f350b4.png) .
See a generalization in [Skopenkov2016k].
.
See a generalization in [Skopenkov2016k].
It would be interesting to know if 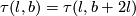 or
or ![[\tau(l,b)]=[\tau(l,b+2l)]\in E_{PS}^7(S^1\times S^3)](/images/math/d/7/b/d7b713e8b6395ebb85e31a2581f01169.png) for any
for any 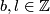 .
.
The unpublished papers [Crowley&Skopenkov2016], [Crowley&Skopenkov2016a] prove that
- any PS embedding
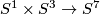 represents
represents ![[\tau(l,b)]\in E_{PS}^7(S^1\times S^3)](/images/math/3/1/d/31d7620d059a56497fbc1f31b238bd9c.png) for some
for some 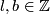 .
.
- any smooth embedding
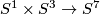 represents
represents 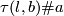 for some
for some 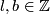 and
and 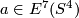 .
.
Example 2.4 (The Lambrechts torus). There is an embedding 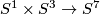 whose complement is not homotopy equivalent to the complement of the standard embedding.
whose complement is not homotopy equivalent to the complement of the standard embedding.
I learned this simple construction from P. Lambrechts.
Take the Hopf fibration 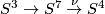 . Take the Hopf linking
. Take the Hopf linking 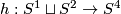 [Skopenkov2016h, Example 2.1]. Then
[Skopenkov2016h, Example 2.1]. Then
Tex syntax error
Tex syntax errorfor
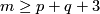 by induction on
by induction on 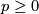 using the following observation: if
using the following observation: if 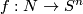 is an embedding, then
is an embedding, then Tex syntax error.
(I conjecture that 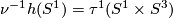 .)
.)
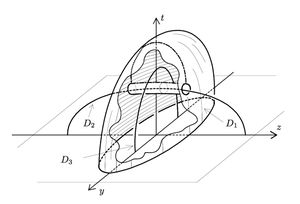
Example 2.5 (the Haefliger torus).
There is a PL embedding 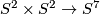 which is not PS isotopic to a smooth embedding.
which is not PS isotopic to a smooth embedding.
Take the Haefliger trefoil knot 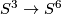 [Skopenkov2016t, Example 2.1]. Extend it to a PL conical embedding
[Skopenkov2016t, Example 2.1]. Extend it to a PL conical embedding 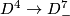 . By [Haefliger1962,
. By [Haefliger1962,  4.2] the trefoil knot also extends to a proper smooth embedding into
4.2] the trefoil knot also extends to a proper smooth embedding into 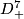 of the punctured torus (or disk with handle), see Figure 1.
These two extensions together form the required PL embedding
of the punctured torus (or disk with handle), see Figure 1.
These two extensions together form the required PL embedding 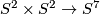 , see Figure 2 for
, see Figure 2 for 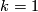 .
By [Boechat&Haefliger1970, p.165] this PL embedding is not PS isotopic to a smooth embedding.
.
By [Boechat&Haefliger1970, p.165] this PL embedding is not PS isotopic to a smooth embedding.
For a higher-dimensional generalization see [Boechat1971, 6.2].
3 Embeddings of the complex projective plane
Example 3.1 [Boechat&Haefliger1970, p.164].
There is an embedding  .
.
Recall that 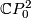 is the mapping cylinder of the Hopf fibration
is the mapping cylinder of the Hopf fibration 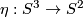 . Recall that
. Recall that 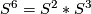 . Define an embedding
. Define an embedding 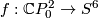 by
by ![f[(x,t)]:=[(x,\eta(x),t)]](/images/math/b/7/0/b7085320f1d3f79b0a9593293e4952d1.png) , where
, where 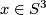 . In other words, the segment joining
. In other words, the segment joining  and
and  is mapped onto the arc in
is mapped onto the arc in  joining
joining  to
to 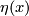 . Clearly, the boundary 3-sphere of
. Clearly, the boundary 3-sphere of 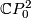 is standardly embedded into
is standardly embedded into  . Hence
. Hence  extends to an embedding
extends to an embedding  .
.
Alternatively, define an embedding  by
by
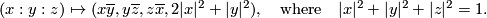
Theorem 3.2. (a) There is only one embedding  up to isotopy and a hyperplane reflection of
up to isotopy and a hyperplane reflection of 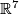 .
In other words, there are exactly two isotopy classes of embeddings
.
In other words, there are exactly two isotopy classes of embeddings  (differing by
composition with a hyperplane reflection of
(differing by
composition with a hyperplane reflection of 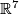 ).
).
(b) For any pair of embeddings 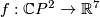 and
and 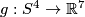 the embedding
the embedding 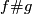 is isotopic to
is isotopic to  .
.
(c) The Boechat-Haefliger invariant (defined below) is an injection 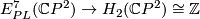 whose image is the set of odd integeres. However, any PL embedding whose Boechat-Haefliger is different from
whose image is the set of odd integeres. However, any PL embedding whose Boechat-Haefliger is different from 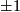 is not smoothable.
is not smoothable.
Parts (a) and (b) are proved in [Skopenkov2005, Triviality Theorem (a)] (they also follow by Theorem 5.3 below). Part (c) follows by [Boechat&Haefliger1970, Theorems 1.6 and 2.1] and Corollary 5.6(b) below.
4 The Boechat-Haefliger invariant
We give definitions in more generality because this is natural and is required for 3-manifolds in 6-space [Skopenkov2016t].
Let  be a closed connected orientable
be a closed connected orientable  -manifold and
-manifold and  an embedding.
Fix an orientation on
an embedding.
Fix an orientation on  and an orientation on
and an orientation on  .
.
Definition 4.1. The composition
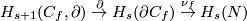
of the boundary map 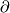 and the projection
and the projection 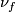 is an isomorphism.
This is well-known, see [Skopenkov2008,
is an isomorphism.
This is well-known, see [Skopenkov2008,  2, the Alexander Duality Lemma].
The inverse
2, the Alexander Duality Lemma].
The inverse 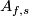 to this composition is `the homology Alexander Duality isomorphism'; it equals to the composition
to this composition is `the homology Alexander Duality isomorphism'; it equals to the composition 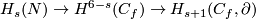 of the cohomology Alexander and Poincaré duality isomorphisms.
of the cohomology Alexander and Poincaré duality isomorphisms.
This is not to be confused with another well-known homology Alexander duality isomorphism 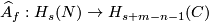 [Skopenkov2005, Alexander Duality Lemma 4.6].
[Skopenkov2005, Alexander Duality Lemma 4.6].
Definition 4.2.
A `homology Seifert surface' for  is the image
is the image ![A_{f,n}[N]\in H_{n+1}(C_f,\partial)](/images/math/b/b/e/bbe031cbd632f67fecc9cdfee925baf6.png) of the fundamental class
of the fundamental class ![[N]](/images/math/3/5/8/3581986b0e7b591acd8d60e6ee096f5d.png) .
.
Denote by  the intersection products
the intersection products 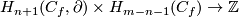 and
and 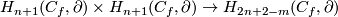 .
.
Remark 4.3.
Take a small oriented disk 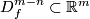 whose intersection with
whose intersection with 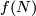 consists of exactly one point of sign
consists of exactly one point of sign 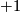 and such that
and such that 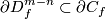 .
A homology Seifert surface
.
A homology Seifert surface 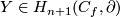 for
for  is uniquely defined by the condition
is uniquely defined by the condition ![Y\cap [\partial D^{m-n}_f]=1](/images/math/b/2/8/b2809249f9928cd86ff2647466969b3e.png) .
.
Definition 4.4.
Define `the Boechat-Haefliger invariant' of 
![\displaystyle \varkappa(f):=A_{f,2n+1-m}^{-1}\left(A_{f,n}[N]\cap A_{f,n}[N]\right)\in H_{2n+1-m}(N).](/images/math/6/9/1/691237d46ac79e4465fe5e708e568f66.png)
Clearly, a map 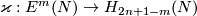 is well-defined by
is well-defined by ![\varkappa([f]):=\varkappa(f)](/images/math/d/1/e/d1ea1467c6e1f7b9ab48975d672905a4.png) .
.
Remark 4.5.
(a) If  , then
, then 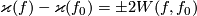 for any two embeddings
for any two embeddings 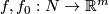 [Skopenkov2008,
[Skopenkov2008,  2, The Boechat-Haefliger Invariant Lemma].
Here
2, The Boechat-Haefliger Invariant Lemma].
Here  is the Whitney invariant [Skopenkov2016e,
is the Whitney invariant [Skopenkov2016e,  5], [Skopenkov2006,
5], [Skopenkov2006,  2].
We conjecture that this holds when
2].
We conjecture that this holds when  is odd and that
is odd and that 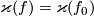 when
when  is even.
is even.
(b) Definition 4.4 is equivalent to the original one for 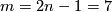 [Boechat&Haefliger1970] by [Crowley&Skopenkov2008, Section Lemma 3.1].
Earlier notation for
[Boechat&Haefliger1970] by [Crowley&Skopenkov2008, Section Lemma 3.1].
Earlier notation for 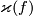 was
was 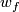 [Boechat&Haefliger1970],
[Boechat&Haefliger1970], 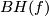 [Skopenkov2005] and
[Skopenkov2005] and 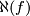 [Crowley&Skopenkov2008].
[Crowley&Skopenkov2008].
5 Classification
We use Stiefel-Whitney characteristic classes 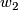 and (for non-orientable 4-manifolds)
and (for non-orientable 4-manifolds) 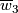 .
.
Theorem 5.1. (a) Any closed orientable 4-manifold embeds into 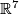 .
.
(b) A closed 4-manifold  embeds into
embeds into 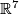 if and only if
if and only if 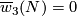 .
.
The PL version of (a) was proved in [Hirsch1965].
It was noticed in [Fuquan1994, p. 447] that the smooth version of (a) easily follows from Theorem 5.3.a below by [Donaldson1987].
(The smooth version of (a) also follows from (b) because 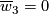 for orientable 4-manifolds [Massey1960].)
The smooth version of (b) is [Fuquan1994, Main Theorem A].
The PL version of (b) follows from the smooth version by the second paragraph of Remark 1.1.
A simpler proof of the PL versions of (b) is given as the proof of [Skopenkov1997, Corollary 1.3.a] (for specialists recall that
for orientable 4-manifolds [Massey1960].)
The smooth version of (b) is [Fuquan1994, Main Theorem A].
The PL version of (b) follows from the smooth version by the second paragraph of Remark 1.1.
A simpler proof of the PL versions of (b) is given as the proof of [Skopenkov1997, Corollary 1.3.a] (for specialists recall that
 for a closed 4-manifold
for a closed 4-manifold  ).
).
Any compact connected nonclosed 4-manifold embeds into 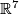 . This follows by taking a 3-spine
. This follows by taking a 3-spine  of
of  ,
bringing a map
,
bringing a map 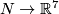 to general position on
to general position on  and restricting the obtained map to sufficiently thin neighborhood of
and restricting the obtained map to sufficiently thin neighborhood of  in
in  ; this neighborhood is homeomorphic to
; this neighborhood is homeomorphic to  .
.
For the classical classification
in the PL category which uses the assumption 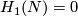 see [Skopenkov2016e], [Skopenkov2006, Theorem 2.13].
see [Skopenkov2016e], [Skopenkov2006, Theorem 2.13].
Theorem 5.2. There is an isomorphism 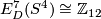 .
.
This is stated in [Haefliger1966, the last line] and follows by [Haefliger1966, 4.11] together with well-known fact 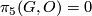 [Skopenkov2005, Lemma 3.1]. For alternative proofs see [Skopenkov2005,
[Skopenkov2005, Lemma 3.1]. For alternative proofs see [Skopenkov2005,  3,
3,  4] and [Crowley&Skopenkov2008, Corollary 1.2.a].
4] and [Crowley&Skopenkov2008, Corollary 1.2.a].
Let  be a closed connected oriented 4-manifold.
be a closed connected oriented 4-manifold.
Tex syntax errorof the Boéchat-Haefliger invariant
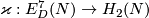
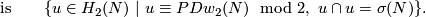
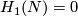 , then for any
, then for any Tex syntax errorthere is an injective invariant called the Kreck invariant,
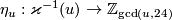
whose image is the subset of even elements.
Here
-
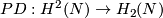 is Poincaré isomorphism.
is Poincaré isomorphism.
-
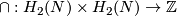 is the intersection form and
is the intersection form and 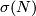 its signature.
its signature.
-
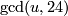 is the maximal integer
is the maximal integer  such that both
such that both 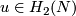 and 24 are divisible by
and 24 are divisible by  .
.
-
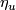 is defined in [Crowley&Skopenkov2008,
is defined in [Crowley&Skopenkov2008,  2].
2].
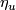 is surjective if
is surjective if  is not divisible by 2. Note that
is not divisible by 2. Note that Tex syntax erroris divisible by 2 (for some
 or, equivalently, for any
or, equivalently, for any  ) if and only if
) if and only if  is spin.
is spin.
If 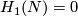 , then all isotopy classes of embeddings
, then all isotopy classes of embeddings 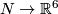 can be constructed from a certain given embedding using
unlinked and
linked embedded connected sum with embeddings
can be constructed from a certain given embedding using
unlinked and
linked embedded connected sum with embeddings 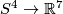 [Skopenkov2016c,
[Skopenkov2016c,  4], [Skopenkov2016e,
4], [Skopenkov2016e,  3].
3].
For a classification when 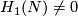 see [Crowley&Skopenkov2016] and unpublished paper [Crowley&Skopenkov2016a].
see [Crowley&Skopenkov2016] and unpublished paper [Crowley&Skopenkov2016a].
Corollary 5.4 ([Crowley&Skopenkov2008, Corollary 1.2]).
(a) There are exactly twelve isotopy classes of embeddings 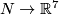 if
if  is an integral homology 4-sphere (cf. Theorem 5.2).
is an integral homology 4-sphere (cf. Theorem 5.2).
(b) Identify 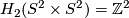 using the standard basis.
For any integer
using the standard basis.
For any integer  there are exactly
there are exactly 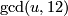 isotopy classes of embeddings
isotopy classes of embeddings 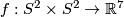 with
with 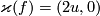 , and the same holds for those with
, and the same holds for those with 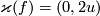 .
Other values of
.
Other values of 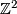 are not in the image of
are not in the image of 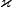 .
.
Addendum 5.5 ([Crowley&Skopenkov2008, Addendum 1.3]).
If 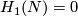 and
and 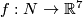 ,
, 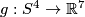 are embeddings, then
are embeddings, then
![\displaystyle \varkappa(f\#g)=\varkappa(f)\quad\text{and}\quad\eta_{\varkappa(f)}[f\#g]\equiv\eta_{\varkappa(f)}[f]+\eta_0[g]\mod\gcd(\varkappa(f),24).](/images/math/8/e/f/8ef791869e2357d46b1a44d6fc8102e1.png)
The following corollary gives examples where the embedded connected sum action of 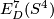 on
on 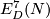 is trivial and where it is effective.
is trivial and where it is effective.
Corollary 5.6 ([Crowley&Skopenkov2008, Corollary 1.4]).
(a) Take an integer  and the Hudson torus
and the Hudson torus 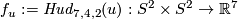 defined in Remark 3.5.d of [Skopenkov2016e], [Skopenkov2006, Example 2.10]. If
defined in Remark 3.5.d of [Skopenkov2016e], [Skopenkov2006, Example 2.10]. If 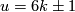 , then for any embedding
, then for any embedding 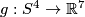 the embedding
the embedding 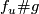 is isotopic to
is isotopic to 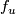 . Moreover, for any integer
. Moreover, for any integer  the number of isotopy classes of embeddings
the number of isotopy classes of embeddings 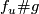 is
is 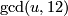 .
.
(b) If 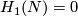 and
and 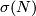 is not divisible by the square of an integer
is not divisible by the square of an integer 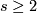 .
Then for any pair of embeddings
.
Then for any pair of embeddings 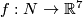 and
and 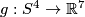 the embedding
the embedding 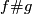 is isotopic to
is isotopic to  ; in other words,
; in other words, 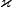 is injective.
is injective.
(c) If 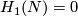 and
and 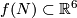 for an embedding
for an embedding 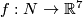 , then for every embedding
, then for every embedding 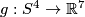 the embedding
the embedding 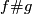 is not isotopic to
is not isotopic to  .
.
We remark that Corollary 5.6(b) was first proved in [Skopenkov2005, The triviality Theorem 1.1] independently of Theorem 5.3.
6 References
- [Boechat&Haefliger1970] J. Boéchat and A. Haefliger, Plongements différentiables des variétés orientées de dimension
 dans
dans 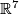 , (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
, (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
- [Boechat1971] J. Boéchat, Plongements de variétées différentiables orientées de dimension
 dans
dans 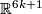 , Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
, Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
- [Crowley&Skopenkov2008] D. Crowley and A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, II, Intern. J. Math., 22:6 (2011) 731-757. Available at the arXiv:0808.1795.
- [Crowley&Skopenkov2016] D. Crowley and A. Skopenkov, Embeddings of non-simply-connected 4-manifolds in 7-space, I. Classification modulo knots, Moscow Math. J., 21 (2021), 43--98. arXiv:1611.04738.
- [Crowley&Skopenkov2016a] D. Crowley and A. Skopenkov, Embeddings of non-simply-connected 4-manifolds in 7-space, II. Smooth classification. Proc. A of the Royal Soc. of Edinburgh, to appear. arXiv:1612.04776
- [Donaldson1987] S. K. Donaldson, The orientation of Yang-Mills moduli spaces and
 -manifold topology, J. Differential Geom. 26 (1987), no.3, 397–428. MR910015 (88j:57020) Zbl 0683.57005
-manifold topology, J. Differential Geom. 26 (1987), no.3, 397–428. MR910015 (88j:57020) Zbl 0683.57005
- [Fuquan1994] F. Fuquan, Embedding four manifolds in
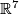 , Topology 33 (1994), 447-454.
, Topology 33 (1994), 447-454.
- [Haefliger1962] A. Haefliger, Knotted
 -spheres in
-spheres in 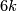 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1966] A. Haefliger, Differential embeddings of
 in
in  for
for  , Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
, Ann. of Math. (2) 83 (1966), 402–436. MR0202151 (34 #2024) Zbl 0151.32502
- [Haefliger1967] A. Haefliger, Lissage des immersions-I, Topology, 6 (1967) 221--240.
- [Hirsch1965] M. W. Hirsch, On embedding 4-manifolds in
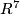 , Proc. Camb. Phil. Soc. 61 (1965).
, Proc. Camb. Phil. Soc. 61 (1965).
- [Mandelbaum1980] R. Mandelbaum, Four-Dimensional Topology: An introduction, Bull. Amer. Math. Soc. (N.S.) 2 (1980) 1-159.
- [Massey1960] W. S. Massey, On the Stiefel--Whitney classes of a manifold, I, Amer. J. Math. 82 (1960), 92-102.
- [Milnor&Stasheff1974] J. W. Milnor and J. D. Stasheff, Characteristic classes, Princeton University Press, Princeton, N. J., 1974. MR0440554 (55 #13428) Zbl 1079.57504
- [Skopenkov1997] A. Skopenkov, On the deleted product criterion for embeddability of manifolds in
 , Comment. Math. Helv. 72 (1997), 543-555.
, Comment. Math. Helv. 72 (1997), 543-555.
- [Skopenkov2002] A. Skopenkov, On the Haefliger-Hirsch-Wu invariants for embeddings and immersions., Comment. Math. Helv. 77 (2002), no.1, 78-124. MRMR1898394 (2003c:57023) Zbl 1012.57035
- [Skopenkov2005] A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, Topol. Appl., 157 (2010) 2094-2110. Available at the arXiv:0512594.
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2008] A. Skopenkov, A classification of smooth embeddings of 3-manifolds in 6-space, Math. Z. 260 (2008), no.3, 647–672. Available at the arXiv:0603429MR2434474 (2010e:57028) Zbl 1167.57013
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016e] A. Skopenkov, Embeddings just below the stable range: classification, to appear in Bull. Man. Atl.
- [Skopenkov2016h] A. Skopenkov, High codimension links, to appear in Bull. Man. Atl.
- [Skopenkov2016k] A. Skopenkov, Knotted tori, preprint.
- [Skopenkov2016t] A. Skopenkov, 3-manifolds in 6-space, to appear in Boll. Man. Atl.