Embeddings in Euclidean space: plan and convention
Askopenkov (Talk | contribs) |
m (Redirected page to Embeddings in Euclidean space: an introduction to their classification#Notation and conventions) |
||
| Line 1: | Line 1: | ||
| + | #REDIRECT [[Embeddings in Euclidean space: an introduction to their classification#Notation_and_conventions]] | ||
{{Authors|Askopenkov}} | {{Authors|Askopenkov}} | ||
== Introduction == | == Introduction == | ||
Latest revision as of 02:42, 8 April 2020
- REDIRECT Embeddings in Euclidean space: an introduction to their classification#Notation_and_conventions
|
The user responsible for this page is Askopenkov. No other user may edit this page at present. |
Contents |
1 Introduction
This page gives references to pages on the classification of embeddings, and introduces notation and conventions used there.
2 References to pages on the classification of embeddings
Here is the introductory article:
Below we list references to information about the classification of embeddings of manifolds into Euclidean space.
The first list is structured by the dimension of the source manifold and the target Euclidean space:
Information structured by the `complexity' of the source manifold:
For more information see e.g. [Skopenkov2006].
3 Notation and conventions
The following notations and conventions will be used in some other pages about embeddings, including those listed in  2.
2.
For a manifold  let
let 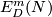 or
or 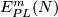 denote the set of
smooth or piecewise-linear (PL) embeddings
denote the set of
smooth or piecewise-linear (PL) embeddings  up to smooth or PL isotopy.
If the category is omitted, then the result holds (or a definition or a construction is given) in both categories.
up to smooth or PL isotopy.
If the category is omitted, then the result holds (or a definition or a construction is given) in both categories.
The sources of all embeddings are assumed to be compact.
Let  be a closed
be a closed  -ball in a closed connected
-ball in a closed connected  -manifold
-manifold  . Denote
. Denote 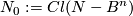 .
.
Let 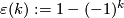 be
be  for
for  even and
even and  for
for  odd, so that
odd, so that 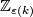 is
is  for
for  even and
even and  for
for  odd.
odd.
Denote by 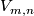 the Stiefel manifold of orthonormal
the Stiefel manifold of orthonormal  -frames in
-frames in  .
.
We omit  -coefficients from the notation of (co)homology groups.
-coefficients from the notation of (co)homology groups.
For a manifold  with boundary
with boundary 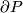 denote
denote 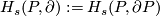 .
.
A closed manifold  is called homologically
is called homologically  -connected, if
-connected, if  is connected and
is connected and 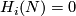 for every
for every 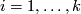 .
This condition is equivalent to
.
This condition is equivalent to 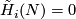 for each
for each  , where
, where 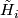 are reduced homology groups.
A pair
are reduced homology groups.
A pair 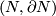 is called homologically
is called homologically  -connected, if
-connected, if 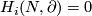 for every
for every  .
.
The self-intersection set of a map 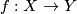 is
is 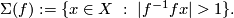
For a smooth embedding  denote by
denote by
-
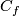 the closure of the complement in
the closure of the complement in 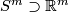 to a tight enough tubular neighborhood of
to a tight enough tubular neighborhood of  and
and
-
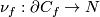 the restriction of the linear normal bundle of
the restriction of the linear normal bundle of  to the subspace of unit length vectors identified with
to the subspace of unit length vectors identified with 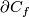 .
.
-
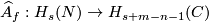 and
and 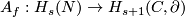 the homological Alexander duality isomorphisms, see the well-known Alexander Duality Lemmas of [Skopenkov2008], [Skopenkov2005].
the homological Alexander duality isomorphisms, see the well-known Alexander Duality Lemmas of [Skopenkov2008], [Skopenkov2005].
4 References
- [Skopenkov2005] A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, Topol. Appl., 157 (2010) 2094-2110. Available at the arXiv:0512594.
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2008] A. Skopenkov, A classification of smooth embeddings of 3-manifolds in 6-space, Math. Z. 260 (2008), no.3, 647–672. Available at the arXiv:0603429MR2434474 (2010e:57028) Zbl 1167.57013
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016e] A. Skopenkov, Embeddings just below the stable range: classification, to appear in Bull. Man. Atl.
- [Skopenkov2016f] A. Skopenkov, 4-manifolds in 7-space, to appear in Bull. Man. Atl.
- [Skopenkov2016h] A. Skopenkov, High codimension links, to appear in Bull. Man. Atl.
- [Skopenkov2016k] A. Skopenkov, Knotted tori, preprint.
- [Skopenkov2016t] A. Skopenkov, 3-manifolds in 6-space, to appear in Boll. Man. Atl.
For a manifold  let
let 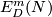 or
or 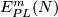 denote the set of
smooth or piecewise-linear (PL) embeddings
denote the set of
smooth or piecewise-linear (PL) embeddings  up to smooth or PL isotopy.
If the category is omitted, then the result holds (or a definition or a construction is given) in both categories.
up to smooth or PL isotopy.
If the category is omitted, then the result holds (or a definition or a construction is given) in both categories.
The sources of all embeddings are assumed to be compact.
Let  be a closed
be a closed  -ball in a closed connected
-ball in a closed connected  -manifold
-manifold  . Denote
. Denote 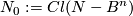 .
.
Let 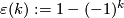 be
be  for
for  even and
even and  for
for  odd, so that
odd, so that 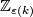 is
is  for
for  even and
even and  for
for  odd.
odd.
Denote by 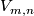 the Stiefel manifold of orthonormal
the Stiefel manifold of orthonormal  -frames in
-frames in  .
.
We omit  -coefficients from the notation of (co)homology groups.
-coefficients from the notation of (co)homology groups.
For a manifold  with boundary
with boundary 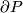 denote
denote 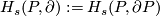 .
.
A closed manifold  is called homologically
is called homologically  -connected, if
-connected, if  is connected and
is connected and 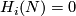 for every
for every 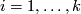 .
This condition is equivalent to
.
This condition is equivalent to 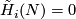 for each
for each  , where
, where 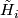 are reduced homology groups.
A pair
are reduced homology groups.
A pair 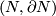 is called homologically
is called homologically  -connected, if
-connected, if 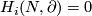 for every
for every  .
.
The self-intersection set of a map 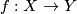 is
is 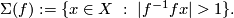
For a smooth embedding  denote by
denote by
-
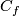 the closure of the complement in
the closure of the complement in 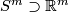 to a tight enough tubular neighborhood of
to a tight enough tubular neighborhood of  and
and
-
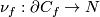 the restriction of the linear normal bundle of
the restriction of the linear normal bundle of  to the subspace of unit length vectors identified with
to the subspace of unit length vectors identified with 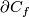 .
.
-
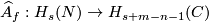 and
and 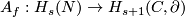 the homological Alexander duality isomorphisms, see the well-known Alexander Duality Lemmas of [Skopenkov2008], [Skopenkov2005].
the homological Alexander duality isomorphisms, see the well-known Alexander Duality Lemmas of [Skopenkov2008], [Skopenkov2005].
4 References
- [Skopenkov2005] A. Skopenkov, A classification of smooth embeddings of 4-manifolds in 7-space, Topol. Appl., 157 (2010) 2094-2110. Available at the arXiv:0512594.
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2008] A. Skopenkov, A classification of smooth embeddings of 3-manifolds in 6-space, Math. Z. 260 (2008), no.3, 647–672. Available at the arXiv:0603429MR2434474 (2010e:57028) Zbl 1167.57013
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016e] A. Skopenkov, Embeddings just below the stable range: classification, to appear in Bull. Man. Atl.
- [Skopenkov2016f] A. Skopenkov, 4-manifolds in 7-space, to appear in Bull. Man. Atl.
- [Skopenkov2016h] A. Skopenkov, High codimension links, to appear in Bull. Man. Atl.
- [Skopenkov2016k] A. Skopenkov, Knotted tori, preprint.
- [Skopenkov2016t] A. Skopenkov, 3-manifolds in 6-space, to appear in Boll. Man. Atl.