Covariant derivative
m (→Definition) |
|||
| (5 intermediate revisions by one user not shown) | |||
| Line 3: | Line 3: | ||
<wikitex>; | <wikitex>; | ||
Let $E \to M$ be a vector bundle over a smooth manifold $M$ | Let $E \to M$ be a vector bundle over a smooth manifold $M$ | ||
| − | and $\Gamma E$ the space of smooth sections. A | + | and $\Gamma E$ the space of smooth sections. A ''covariant derivative'' |
on $E$ is a bilinear map $\nabla : \Gamma TM \times \Gamma E \to \Gamma E$, $(X,s)\mapsto\nabla_Xs$, | on $E$ is a bilinear map $\nabla : \Gamma TM \times \Gamma E \to \Gamma E$, $(X,s)\mapsto\nabla_Xs$, | ||
which is a [[Tensor|tensor]] (linear over $C^\infty(M)$) in the first argument and | which is a [[Tensor|tensor]] (linear over $C^\infty(M)$) in the first argument and | ||
| − | a | + | a ''derivation'' in the second argument: |
| − | + | \begin{equation} \begin{matrix}\nabla_{(fX)}s &=& f\nabla_Xs\, \\ \nabla_{X}(fs) &=& (Xf)s + f\nabla_Xs \,,\end{matrix} \end{equation} | |
where $f$ is a smooth function and $X$ a vector field on $M$ and $s$ a section of $E$, and where | where $f$ is a smooth function and $X$ a vector field on $M$ and $s$ a section of $E$, and where | ||
$Xf = \partial_Xf = df.X$ is the ordinary derivative of the function $f$ in the direction of $X$. By these | $Xf = \partial_Xf = df.X$ is the ordinary derivative of the function $f$ in the direction of $X$. By these | ||
| Line 22: | Line 22: | ||
Covariant derivatives are not ''tensors'' since they are derivations in the second argument, but | Covariant derivatives are not ''tensors'' since they are derivations in the second argument, but | ||
| − | two covariant | + | two covariant derivatives $\nabla,\tilde\nabla$ on $E$ differ by a tensor: |
$A = \tilde\nabla-\nabla$ defines a tensor $A \in \textup{Hom}(TM\otimes E,E)$. | $A = \tilde\nabla-\nabla$ defines a tensor $A \in \textup{Hom}(TM\otimes E,E)$. | ||
</wikitex> | </wikitex> | ||
| + | == Examples== | ||
| + | <wikitex>; | ||
| + | * The [[Levi-Civita connection|Levi-Civita derivative]] on $TM$ where $M$ is a Riemannian manifold | ||
| + | * The [[Canonical connection|Canonical derivative]] on $TM$ where $M = G/H$ is a reductive homogeneous space | ||
| + | * The ''Projection derivative'' on a subbundle $E \subset M \times \Rr^n$: For any $s \in \Gamma E \subset C^\infty(M,\Rr^n)$ | ||
| + | and a local parametrization $\phi$ on $M$ we put | ||
| + | $$ | ||
| + | \nabla_i s = (\partial_is)^E | ||
| + | $$ | ||
| + | where $(\,\,)^E$ at any point $p\in M$ denotes the orthogonal projection from $\Rr^n$ onto the subspace $E_p$. | ||
| + | |||
| + | For further information see \cite{Kobayashi&Nomizu1963}. | ||
| + | </wikitex> | ||
== References== | == References== | ||
{{#RefList:}} | {{#RefList:}} | ||
[[Category:Definitions]] | [[Category:Definitions]] | ||
| + | [[Category:Connections and curvature]] | ||
Latest revision as of 08:20, 28 May 2013
|
The user responsible for this page is Jost Eschenburg. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Definition
Let 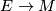 be a vector bundle over a smooth manifold
be a vector bundle over a smooth manifold  and
and 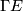 the space of smooth sections. A covariant derivative
on
the space of smooth sections. A covariant derivative
on  is a bilinear map
is a bilinear map 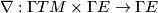 ,
, 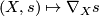 ,
which is a tensor (linear over
,
which is a tensor (linear over 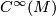 ) in the first argument and
a derivation in the second argument:
) in the first argument and
a derivation in the second argument:
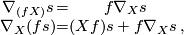
where  is a smooth function and
is a smooth function and  a vector field on
a vector field on  and
and  a section of
a section of  , and where
, and where
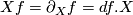 is the ordinary derivative of the function
is the ordinary derivative of the function  in the direction of
in the direction of  . By these
properties,
. By these
properties,  is defined locally and even pointwise regarding the first argument: For any
is defined locally and even pointwise regarding the first argument: For any 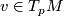 we may define
we may define 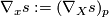 where
where  is any (local) vector field with
is any (local) vector field with 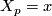 .
.
A covariant derivative has all properties of the ordinary directional derivative
for functions with exception of the commutativity: For functions  we have
we have 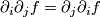 with
with 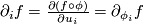 , where
, where 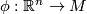 is
a local parametrization of
is
a local parametrization of  and
and 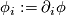 its
its  -th partial derivative. Instead, for covariant derivatives, the commutator
-th partial derivative. Instead, for covariant derivatives, the commutator
![[\nabla_i,\nabla_j]](/images/math/a/a/4/aa465354fd9efac294989bb1ef5bac3d.png) (with
(with 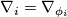 ) is nonzero in general, but it is
only a tensor (rather than a differential operator), the curvature tensor.
) is nonzero in general, but it is
only a tensor (rather than a differential operator), the curvature tensor.
Covariant derivatives are not tensors since they are derivations in the second argument, but
two covariant derivatives 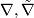 on
on  differ by a tensor:
differ by a tensor:
 defines a tensor
defines a tensor 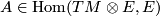 .
.
2 Examples
- The Levi-Civita derivative on
 where
where  is a Riemannian manifold
is a Riemannian manifold
- The Canonical derivative on
 where
where 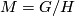 is a reductive homogeneous space
is a reductive homogeneous space
- The Projection derivative on a subbundle
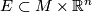 : For any
: For any 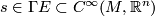
and a local parametrization  on
on  we put
we put
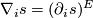
where 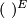 at any point
at any point 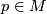 denotes the orthogonal projection from
denotes the orthogonal projection from  onto the subspace
onto the subspace 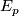 .
.
For further information see [Kobayashi&Nomizu1963].
3 References
- [Kobayashi&Nomizu1963] S. Kobayashi and K. Nomizu, Foundations of differential geometry. Vol I, Interscience Publishers, a division of John Wiley & Sons, New York-London, 1963. MR1393940 (97c:53001a) Zbl 0508.53002