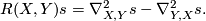Curvature tensor and second derivative
|
The user responsible for this page is Jost Eschenburg. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Definition
Let  be a smooth manifold and
be a smooth manifold and  a vector bundle over
a vector bundle over  with
covariant derivative
with
covariant derivative  . Let
. Let 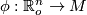 be a
local parametrization of
be a
local parametrization of  , defined on some open subset
, defined on some open subset 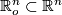 and let
and let 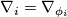 where
where 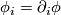 are the
coordinate vector fields. The commutator
are the
coordinate vector fields. The commutator ![[\nabla_i,\nabla_j]](/images/math/a/a/4/aa465354fd9efac294989bb1ef5bac3d.png) is in general
nonzero, but it is no longer a differential operator, but a tensor
is in general
nonzero, but it is no longer a differential operator, but a tensor 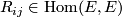 ,
,
![R_{ij}s := [\nabla_i,\nabla_j]s = \nabla_i\nabla_js - \nabla_j\nabla_is](/images/math/e/0/7/e07385894231745e1b0b4fbb9cb41373.png)
for all 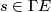 . More generally, for arbitrary vector fields
. More generally, for arbitrary vector fields 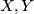 with
with
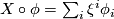 and
and 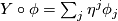 we put
we put
![R(X,Y)s = \sum_{ij} \xi^i\eta^j R_{ij}s = [\nabla_X,\nabla_Y]s - \nabla_{[X,Y]}s](/images/math/a/d/2/ad2e427e6cc5cd8d760f3ac414e3e33e.png)
where ![[X,Y] = \sum_i \left((X\eta^i) - (Y\xi^i)\right)\phi_i](/images/math/a/7/9/a79d8229e34ed9a0c225c5f9b494777e.png) denotes the Lie bracket
of vector fields. This defines a tensor
denotes the Lie bracket
of vector fields. This defines a tensor 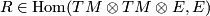 ,
called curvature tensor.
,
called curvature tensor.
If in addition we have any connection  on
on  which is torsion free, we may view
which is torsion free, we may view
 as the antisymmetric part of the second derivative of sections as follows.
The covariant derivative of any section
as the antisymmetric part of the second derivative of sections as follows.
The covariant derivative of any section 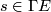 is a tensor
is a tensor  which has again a covariant derivative (tensor derivative)
which has again a covariant derivative (tensor derivative) 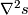 . This defines
a tensor
. This defines
a tensor 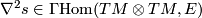 , the second covariant derivative of
, the second covariant derivative of  , with
, with
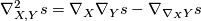
for all 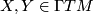 . Since
. Since ![\nabla_XY -\nabla_YX = [X,Y]](/images/math/c/f/9/cf94a20c68b0c630af9a89bc144ca231.png) , we obtain
, we obtain