Canonical connection
|
The user responsible for this page is Jost Eschenburg. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Definition
Let  be a homogeneous space, that is a smooth manifold on which a Lie group
be a homogeneous space, that is a smooth manifold on which a Lie group  acts transitively by diffeomorphisms. Then
acts transitively by diffeomorphisms. Then 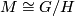 where
where  is the isotropy group of some base point
is the isotropy group of some base point 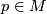 , and the action map
, and the action map 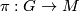 ,
, 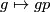 becomes the canonical projection
becomes the canonical projection 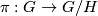 which is a principal bundle with structure group
which is a principal bundle with structure group  . Let
. Let 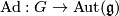 denote the adjoint representation of
denote the adjoint representation of  . Its restriction
. Its restriction 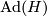 clearly keeps
clearly keeps  invariant. We will assume that the homogeneous space
invariant. We will assume that the homogeneous space 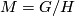 is reductive: there is a vector space complement
is reductive: there is a vector space complement  of
of  in
in 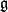 which is also invariant under
which is also invariant under 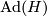 . Reductiveness is often fulfilled; in particular it holds if
. Reductiveness is often fulfilled; in particular it holds if  is compact. Since
is compact. Since 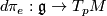 has kernel
has kernel  , it is an isomorphism on the complement
, it is an isomorphism on the complement  , and it carries the representation
, and it carries the representation 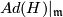 into the isotropy representation of
into the isotropy representation of  on
on 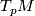 . Via
. Via 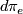 we identify
we identify  with
with 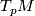 .
.
Using left translations 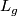 ,
, 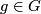 ,
,  defines a distribution
defines a distribution 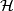 on
on  (the ``horizontal distribution´´
(the ``horizontal distribution´´ 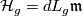 ) which is complementary to the vertical distribution
) which is complementary to the vertical distribution 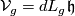 and which is invariant under the right translations of
and which is invariant under the right translations of  if
if  is a reductive complement. Thus
is a reductive complement. Thus  defines a connection on the
defines a connection on the  -principal bundle
-principal bundle 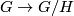 , called the canonical connection of the reductive homogeneous space
, called the canonical connection of the reductive homogeneous space 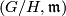 .
.
The canonical connection determines a covariant derivative  on the tangent bundle
on the tangent bundle  since this is associated to
since this is associated to 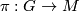 ,
,
![\displaystyle (G\times\mathfrak{m})/H \buildrel \cong \over \longrightarrow TM,\ \ \ [g,X] \mapsto d\pi_g dL_g X,](/images/math/5/f/b/5fbb3e5ca32910b2a590b15fc0fa9d52.png)
where 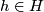 acts on
acts on 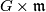 by
by 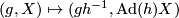 . The covariant derivative
. The covariant derivative  can be defined by its parallel vector fields. A curve
can be defined by its parallel vector fields. A curve 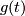 in
in  is the parallel displacement for
is the parallel displacement for  along the path
along the path 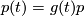 in
in  if and only if it is horizontal,
if and only if it is horizontal, 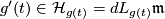 . Thus for every
. Thus for every 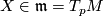 , the vector field
, the vector field 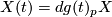 is parallel along the curve
is parallel along the curve 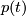 .
.
Since  is a transformation group on
is a transformation group on  , its Lie algebra
, its Lie algebra 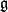 also ``acts´´ on
also ``acts´´ on  by the action vector fields: To each
by the action vector fields: To each 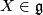 we assign a vector field
we assign a vector field 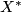 on
on  by putting for each
by putting for each 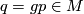
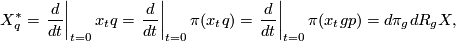
where 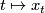 is a curve in
is a curve in  with
with 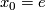 and
and 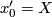 , e.g.
, e.g. 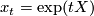 . Thus
. Thus 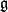 is embedded into the Lie algebra of vector fields on
is embedded into the Lie algebra of vector fields on  . However there is a sign change in the Lie bracket: Note that
. However there is a sign change in the Lie bracket: Note that 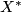 is
is  -related to the right invariant vector field
-related to the right invariant vector field 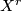 on
on  since
since 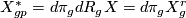 ; thus
; thus ![[X^*,Y^*]](/images/math/2/e/1/2e1404b527941c360120d331fc1d4445.png) is
is  -related to
-related to ![[X^r,Y^r] = -[X,Y]^r](/images/math/5/0/6/5066aa4444394eeac277744ed1854298.png) and therefore
and therefore
![[X^*,Y^*] = -[X,Y]^* .](/images/math/6/5/0/65056c8f178dd9ff0ffd67df2382f3a0.png)
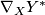 for any
for any 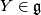 and
and 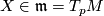 . Putting
. Putting 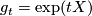 and
and 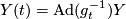 we have
we have 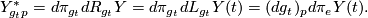
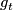 is the parallel transport along the curve
is the parallel transport along the curve 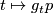 in
in  , we obtain
, we obtain 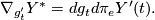 Thus for
Thus for 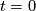 we have
we have
![\nabla_X Y^* = d\pi_e Y'(0) = -d\pi_e[X,Y].](/images/math/b/8/c/b8c0b6cc6f884ba53a029cc6f8eb08f5.png)
From this we may compute the torsion tensor  for any
for any 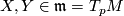 by extending
by extending 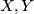 to the action vector fields
to the action vector fields 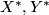 on
on  , using (1), (2):
, using (1), (2):
Tex syntax error
where 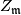 denotes the
denotes the  -component of any
-component of any 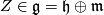 .
.
The  -valued curvature form
-valued curvature form 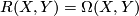 for
for 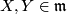 is obtained from the Connections, (7.2):
is obtained from the Connections, (7.2):
![R(X,Y) = \Omega[X,Y] = -[X,Y]_\mathfrak{h},](/images/math/a/d/f/adf54d493430d352331b6be5c30c54c3.png)
where 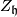 denotes the
denotes the  -component of any
-component of any 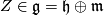 . Since the connection on
. Since the connection on  is invariant under left translations, the action of
is invariant under left translations, the action of  on
on  is affine, that is it preserves the covariant derivative
is affine, that is it preserves the covariant derivative  , and the same is true for the torsion and the curvature tensors,
, and the same is true for the torsion and the curvature tensors,  and
and  . In particular it is preserved under parallel displacements which are horizontal curves in
. In particular it is preserved under parallel displacements which are horizontal curves in  (in particular, the holonomy group of
(in particular, the holonomy group of  is contained in
is contained in  ). Thus these tensors are
). Thus these tensors are  -parallel.
-parallel.
Vice versa, given any manifold  with a connection
with a connection  on
on  with parallel torsion and curvature tensors, then
with parallel torsion and curvature tensors, then  is a reductive locally homogeneous space, i.e. each point
is a reductive locally homogeneous space, i.e. each point 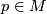 has an open neighborhood which can be identified to some set in a reductive homogeneous space
has an open neighborhood which can be identified to some set in a reductive homogeneous space 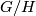 where
where  becomes the canonical connection of
becomes the canonical connection of 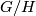 . In fact, let
. In fact, let 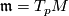 and
and 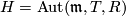 the group of automorphisms of
the group of automorphisms of  preserving both the ``product´´
preserving both the ``product´´ 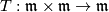 and the ``triple product´´
and the ``triple product´´ 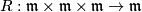 . Then
. Then  is a Lie group with Lie algebra
is a Lie group with Lie algebra 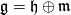 where
where 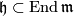 is the Lie algebra of
is the Lie algebra of  and where the remaining Lie brackets are given as follows:
and where the remaining Lie brackets are given as follows:
![[A,X] = AX,\ \ \ [X,Y] = -(R(X,Y)+T(X,Y)) \in \mathfrak{h} \oplus \mathfrak{m}= \mathfrak{g}](/images/math/e/9/d/e9d99ba74a8e4d95e48971402d3f3630.png)
for all 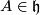 and
and 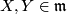 .
.
When ![[\mathfrak{m},\mathfrak{m}] \subset \mathfrak{h}](/images/math/b/9/e/b9e0da311c749b79a19b73e2593b75aa.png) , these spaces are called locally symmetric. This happens if and only if the torsion tensor
, these spaces are called locally symmetric. This happens if and only if the torsion tensor ![T = [\mathfrak{m},\mathfrak{m}]_\mathfrak{m}](/images/math/c/a/4/ca4031b9eed0ad06510bd486129c3de8.png) vanishes. Moreover, if
vanishes. Moreover, if 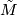 carries a
carries a  -invariant (semi-)Riemannian metric, the canonical connection
-invariant (semi-)Riemannian metric, the canonical connection  preserves the metric and is torsion free, hence it is the Levi-Civita connection of
preserves the metric and is torsion free, hence it is the Levi-Civita connection of 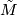 .
.
2 Example
 be the set of all real positive definite symmetric
be the set of all real positive definite symmetric 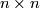 -matrices which is an open subset of the space of all symmetric matrices,
-matrices which is an open subset of the space of all symmetric matrices, 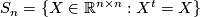 . The group
. The group 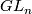 acts transitively on
acts transitively on  by
by 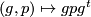 . The isotropy group of
. The isotropy group of 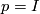 (unit matrix) is the orthogonal group
(unit matrix) is the orthogonal group 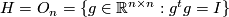 whose Lie algebra is the space of antisymmetric matrices,
whose Lie algebra is the space of antisymmetric matrices, 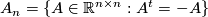 . Thus
. Thus 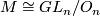 , and the reductive splitting is
, and the reductive splitting is 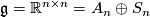 with
with 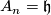 and
and 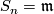 . The vector space
. The vector space 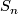 is not a Lie algebra since for the commutator of any
is not a Lie algebra since for the commutator of any 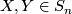 we have
we have ![[X,Y]\in A_n](/images/math/f/2/b/f2b80f004240e3b97b50f767698da38f.png) . But it is a Lie triple: Note that
. But it is a Lie triple: Note that ![[A,X] \in S_n](/images/math/c/9/f/c9feab7a58e86b0d4e0aff4131f4cd03.png) for all
for all 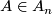 ,
, 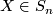 (since
(since 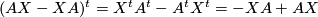 ), in particular
), in particular ![[[X,Y],Z] \in S_n](/images/math/b/3/b/b3be2d1403e79e74c27313e4a2ebebb8.png) for all
for all 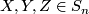 . The canonical connection is torsion free (i.e.
. The canonical connection is torsion free (i.e.  is symmetric) since
is symmetric) since ![[\mathfrak{m},\mathfrak{m}]\subset\mathfrak{h}](/images/math/a/6/1/a61a6994b8dd6c724cb4503cfe61ea11.png) , and its curvature tensor is
, and its curvature tensor is ![R(X,Y)Z = - [[X,Y],Z]](/images/math/d/8/6/d867ed24fe9b576e1eb237eba2e0de16.png) . The trace metric on
. The trace metric on 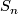 is invariant under
is invariant under 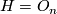 and extends to a
and extends to a 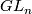 -invariant Riemannian metric on
-invariant Riemannian metric on  given as follows: For any
given as follows: For any 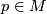 and
and 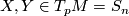 we put
we put 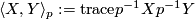
 with respect to this metric. The sectional curvature is nonpositive; it is given by
with respect to this metric. The sectional curvature is nonpositive; it is given by ![\langle R(X,Y)Y,X\rangle = -\textup{trace}([[X,Y],Y]X) = \textup{trace}[X,Y]^2 \leq 0](/images/math/3/9/1/391ee98aa615fb353efa8a9c5a4cd3c0.png) (recall that
(recall that ![[X,Y] \in A_n](/images/math/7/6/0/76052aa65fc5ed2b5e79ac96e72d8701.png) has imaginary eigenvalues, hence its square has nonpositive trace).
has imaginary eigenvalues, hence its square has nonpositive trace).
For further information, see [Kowalski1980].
3 References
- [Kowalski1980] O. Kowalski, Generalized symmetric spaces, LNM 805, Springer-Verlag, 1980. MR579184 (83d:53036) Zbl 0614.53040