Levi-Civita connection
|
The user responsible for this page is Jost Eschenburg. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Definition
Let  be a smooth manifold with tangent bundle
be a smooth manifold with tangent bundle  .
Let
.
Let 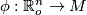 be a local parametrization,
defined on some open domain
be a local parametrization,
defined on some open domain 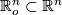 , and let
, and let
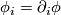 be the partial derivatives; the vectors
be the partial derivatives; the vectors
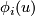 ,
, 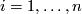 form a basis of
form a basis of 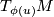 for every
for every 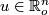 .
.
A semi-Riemannian metric on a  is a linear bundle map
is a linear bundle map
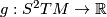 , sometimes called metric tensor,
which is nondegenerate, that is
, sometimes called metric tensor,
which is nondegenerate, that is 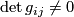 where
where 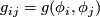 . If
. If  is positive definite,
is positive definite,
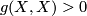 for every nonzero vector field
for every nonzero vector field  on
on  , it is
called a Riemannian metric. A (semi-) Riemannian manifold is
a smooth manifold
, it is
called a Riemannian metric. A (semi-) Riemannian manifold is
a smooth manifold  together with a (semi-)Riemannian metric
together with a (semi-)Riemannian metric  .
.
Every semi-Riemannian manifold 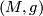 carries a particular affine
connection,
the Levi-Civita connection. This is a covariant derivative
carries a particular affine
connection,
the Levi-Civita connection. This is a covariant derivative
 on the tangent bundle
on the tangent bundle  with the following two properties:
with the following two properties:
- it has no torsion,
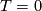 ,
,
- the metric is parallel,
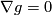 .
.
The second equation involves the covariant derivative of the metric tensor 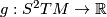 which is defined
in such a way that applications of tensors to vector fields satisfy the Leibniz product rule:
which is defined
in such a way that applications of tensors to vector fields satisfy the Leibniz product rule:
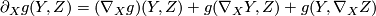
for all 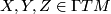 . Thus the rules (1) and (2) can be rephrased as
. Thus the rules (1) and (2) can be rephrased as
-
![\nabla_XY - \nabla_YX = [X,Y]](/images/math/c/9/3/c936f6892f7de0c3e6f59ea9a57c401e.png) ,
,
-
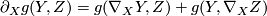 .
.
for all 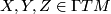 . If the semi-Riemannian metric
. If the semi-Riemannian metric  is fixed, we often write
is fixed, we often write
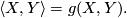
The Levi-Civita connection is uniquely determined by properties (1) and (2) which imply
![\begin{matrix} 2\langle\nabla_XY,Z\rangle &=& X\langle Y, Z\rangle + Y\langle Z,X\rangle - Z\langle X,Y\rangle \\ && -\langle X,[Y,Z]\rangle + \langle Y,[Z,X]\rangle + \langle Z,[X,Y]\rangle \end{matrix}](/images/math/9/9/1/991fad38bc38324459e730b0090a0028.png) (1)
(1)for all 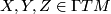 (Koszul formula). If we specialize to the coordinate vector fields
(Koszul formula). If we specialize to the coordinate vector fields 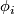 ,
the Lie bracket terms vanish:
,
the Lie bracket terms vanish:
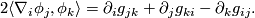
Denoting the coefficents of 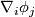 , the so called Christoffel symbols by
, the so called Christoffel symbols by 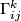 ,
,
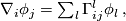 (2)
(2)we obtain the Levi-Civita formula
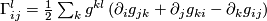 (3)
(3)where 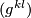 denotes the inverse matrix of the metric coefficient matrix
denotes the inverse matrix of the metric coefficient matrix
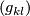 .
.
For further information, see [Milnor1963], [Kobayashi&Nomizu1963] and [O'Neill1983].
2 References
- [Kobayashi&Nomizu1963] S. Kobayashi and K. Nomizu, Foundations of differential geometry. Vol I, Interscience Publishers, a division of John Wiley & Sons, New York-London, 1963. MR1393940 (97c:53001a) Zbl 0508.53002
- [Milnor1963] J. Milnor, Morse theory, Princeton University Press, 1963. MR0163331 (29 #634) Zbl 0108.10401
- [O'Neill1983] B. O'Neill, Semi-Riemannian geometry, Academic Press Inc., 1983. MR719023 (85f:53002) Zbl 0531.53051
3 External links
- The Encyclopedia of Mathematics article on the Levi-Civita connection
- The Wikipedia page on the Levi-Civita connection