Connection on a principal bundle
(→Definition) |
|||
| (One intermediate revision by one user not shown) | |||
| Line 3: | Line 3: | ||
<wikitex include>; | <wikitex include>; | ||
Let $G$ be a Lie group with Lie algebra $\frak{g}$ and | Let $G$ be a Lie group with Lie algebra $\frak{g}$ and | ||
| − | $F \to M$ a [[Principal bundle|principal bundle]] for $G$ over a | + | $F \to M$ a [[Principal bundle of smooth manifolds|principal bundle]] for $G$ over a |
smooth manifold $M$. A ''connection'' on $F$ is a ''distribution'' | smooth manifold $M$. A ''connection'' on $F$ is a ''distribution'' | ||
(a subbundle of the tangent bundle) $\mathcal{H} \subset TF$ | (a subbundle of the tangent bundle) $\mathcal{H} \subset TF$ | ||
| Line 11: | Line 11: | ||
The decomposition $TF = \mathcal{V} \oplus \mathcal{H}$ can be given by the projection | The decomposition $TF = \mathcal{V} \oplus \mathcal{H}$ can be given by the projection | ||
$\pi_\mathcal{V} : TF \to \mathcal{V}$ onto the vertical distribution. Since each vertical | $\pi_\mathcal{V} : TF \to \mathcal{V}$ onto the vertical distribution. Since each vertical | ||
| − | space $\mathcal{V}_f$ can be identified with $\frak{g}$ (see [[Principal bundle]]), | + | space $\mathcal{V}_f$ can be identified with $\frak{g}$ (see [[Principal bundle of smooth manifolds|Principal bundle]]), this map $\pi_V$ can be viewed as a $\frak{g}$-valued 1-form on $F$, |
| − | this map $\pi_V$ can be viewed as a $\frak{g}$-valued 1-form on $F$, | + | |
a linear map $\omega : TF \to \frak{g}$; this is called the ''connection form''. | a linear map $\omega : TF \to \frak{g}$; this is called the ''connection form''. | ||
| Line 19: | Line 18: | ||
A connection $\mathcal{H}$ on a $G$-principal bundles $F$ induces a distribution on any associated | A connection $\mathcal{H}$ on a $G$-principal bundles $F$ induces a distribution on any associated | ||
| − | bundle $E = (F \times E_o)/G$ (see [[Principal bundle]]) since $\mathcal{H}$ passes | + | bundle $E = (F \times E_o)/G$ (see [[Principal bundle of smooth manifolds|Principal bundle]]) since $\mathcal{H}$ passes trivially to $F \times E_o$ and by $G$-invariance to $E$. The induced distribution is called a ''connection on $E$''. If $E_o$ is a vector bundle (the action of $G$ on $E_o$ is linear), the connection on $E$ is closely related to a [[covariant derivative]] (see [[Connections]]). |
| − | trivially to $F \times E_o$ and by $G$-invariance to $E$. The induced distribution is called a ''connection on $E$''. If $E_o$ is a vector bundle (the action of $G$ on $E_o$ is linear), the connection | + | |
| − | on $E$ is closely related to a [[covariant derivative]] (see [[Connections]]). | + | |
</wikitex> | </wikitex> | ||
| + | == Examples == | ||
| + | <wikitex>; | ||
| + | A (semi-)Riemannian metric on $M$ defines a connection on the | ||
| + | orthonormal frame bundle $F$, the [[Levi-Civita connection|''Levi-Civita connection'']]: | ||
| + | The horizontal space $\mathcal{H}_f$ at some orthonormal basis | ||
| + | $f$ of $T_pM$ consists of the derivatives of all curves $f(t)$ in $F$ which are | ||
| + | parallel along their base point curve $p(t)$ in $M$. | ||
| + | |||
| + | Another type of example is the [[Canonical connection|''canonical connection'']] on the principal | ||
| + | bundle $G \to G/H$ of a reductive homogeneous space $M = G/H$. | ||
| + | |||
| + | For further information see \cite{Kobayashi&Nomizu1963}. | ||
== References == | == References == | ||
| Line 28: | Line 37: | ||
[[Category:Definitions]] | [[Category:Definitions]] | ||
| + | [[Category:Connections and curvature]] | ||
Latest revision as of 12:26, 22 May 2013
|
The user responsible for this page is Jost Eschenburg. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Definition
Let  be a Lie group with Lie algebra
be a Lie group with Lie algebra 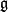 and
and
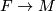 a principal bundle for
a principal bundle for  over a
smooth manifold
over a
smooth manifold  . A connection on
. A connection on  is a distribution
(a subbundle of the tangent bundle)
is a distribution
(a subbundle of the tangent bundle) 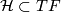 on
on  , called the "horizontal distribution", which is
, called the "horizontal distribution", which is  -invariant and
complementary to the vertical distribution
-invariant and
complementary to the vertical distribution 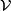 on
on  .
.
The decomposition 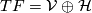 can be given by the projection
can be given by the projection
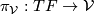 onto the vertical distribution. Since each vertical
space
onto the vertical distribution. Since each vertical
space 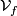 can be identified with
can be identified with 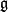 (see Principal bundle), this map
(see Principal bundle), this map 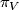 can be viewed as a
can be viewed as a 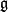 -valued 1-form on
-valued 1-form on  ,
a linear map
,
a linear map 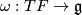 ; this is called the connection form.
; this is called the connection form.
The 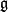 -valued 2-form
-valued 2-form ![\Omega := d\omega + [\omega,\omega]](/images/math/8/9/0/890f4329f822771ebae49340bdf3b095.png) is called curvature form
and measures the non-integrability of the distribution
is called curvature form
and measures the non-integrability of the distribution 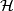 , see the theory page Connections for details.
, see the theory page Connections for details.
A connection 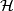 on a
on a  -principal bundles
-principal bundles  induces a distribution on any associated
bundle
induces a distribution on any associated
bundle 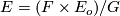 (see Principal bundle) since
(see Principal bundle) since 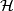 passes trivially to
passes trivially to 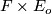 and by
and by  -invariance to
-invariance to  . The induced distribution is called a connection on
. The induced distribution is called a connection on  . If
. If 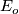 is a vector bundle (the action of
is a vector bundle (the action of  on
on 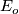 is linear), the connection on
is linear), the connection on  is closely related to a covariant derivative (see Connections).
is closely related to a covariant derivative (see Connections).
2 Examples
A (semi-)Riemannian metric on  defines a connection on the
orthonormal frame bundle
defines a connection on the
orthonormal frame bundle  , the Levi-Civita connection:
The horizontal space
, the Levi-Civita connection:
The horizontal space 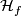 at some orthonormal basis
at some orthonormal basis
 of
of 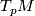 consists of the derivatives of all curves
consists of the derivatives of all curves 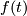 in
in  which are
parallel along their base point curve
which are
parallel along their base point curve 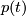 in
in  .
.
Another type of example is the canonical connection on the principal
bundle 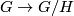 of a reductive homogeneous space
of a reductive homogeneous space 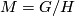 .
.
For further information see [Kobayashi&Nomizu1963].
References
- [Kobayashi&Nomizu1963] S. Kobayashi and K. Nomizu, Foundations of differential geometry. Vol I, Interscience Publishers, a division of John Wiley & Sons, New York-London, 1963. MR1393940 (97c:53001a) Zbl 0508.53002