Connections
|
The user responsible for this page is Jost Eschenburg. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
How can we differentiate a section  in a vector bundle
in a vector bundle  over a manifold
over a manifold  ? It takes values in different vector spaces
? It takes values in different vector spaces 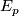 for each
for each 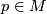 , but differentiating involves comparing values at different points
, but differentiating involves comparing values at different points  . This needs an extra structure on
. This needs an extra structure on  which connects the different vector spaces
which connects the different vector spaces 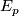 ,
, 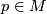 , among each other; it is therefore called connection. It can be defined in two different ways. Either it is viewed as a linear map which assigns to each vector field
, among each other; it is therefore called connection. It can be defined in two different ways. Either it is viewed as a linear map which assigns to each vector field  on
on  a so called covariant derivative, a differential operator
a so called covariant derivative, a differential operator 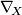 on the space of sections on
on the space of sections on  . Or else it is given as a parallel displacement along curves in
. Or else it is given as a parallel displacement along curves in  : Given two points
: Given two points 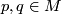 and a curve
and a curve  connecting these points, a connection allows to move any element of
connecting these points, a connection allows to move any element of 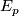 to
to 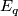 along
along  . Infinitesimally it is given by a distribution
. Infinitesimally it is given by a distribution 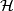 on
on  or on its frame bundle
or on its frame bundle 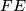 . Let us repeat: In ordinary analysis we differentiate functions with values in a constant vector space; differentiating functions with values in a variable vector space
. Let us repeat: In ordinary analysis we differentiate functions with values in a constant vector space; differentiating functions with values in a variable vector space 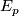 (a vector bundle) needs an extra structure called connection. The greater generality leads to a new notion: curvature. In the covariant derivative model, curvature is the commutator
(a vector bundle) needs an extra structure called connection. The greater generality leads to a new notion: curvature. In the covariant derivative model, curvature is the commutator ![[\nabla_i,\nabla_j]](/images/math/a/a/4/aa465354fd9efac294989bb1ef5bac3d.png) of covariant derivatives in two coordinate directions. For ordinary derivatives
of covariant derivatives in two coordinate directions. For ordinary derivatives 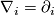 this quantity vanishes, and for covariant derivatives it is an algebraic quantity (a tensor) rather than a differential operator. In the parallel displacement model, curvature is just the non-integrability of the distribution, the tensor
this quantity vanishes, and for covariant derivatives it is an algebraic quantity (a tensor) rather than a differential operator. In the parallel displacement model, curvature is just the non-integrability of the distribution, the tensor ![[\mathcal{H},\mathcal{H}]^{\mathcal{H}^\perp}](/images/math/0/d/3/0d39009ebfe74571b06aeef9f135b9a1.png) . A case of particular importance is the tangent bundle,
. A case of particular importance is the tangent bundle, 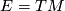 . A connection on
. A connection on  yields a second tensor quantity beneath curvature, the so called torsion. This is explained best by passing to the affine frame bundle; therefore a connection on
yields a second tensor quantity beneath curvature, the so called torsion. This is explained best by passing to the affine frame bundle; therefore a connection on  is sometimes called affine connection.
is sometimes called affine connection.
2 Covariant derivatives
A covariant derivative on a vector bundle  over a smooth manifold
over a smooth manifold  is a directional derivative
is a directional derivative  for sections of
for sections of  . It can be viewed as a bilinear map
. It can be viewed as a bilinear map 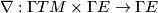 ,
, 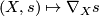 which is a tensor (linear over
which is a tensor (linear over 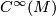 ) in the first argument and a derivation in the second argument:
) in the first argument and a derivation in the second argument:
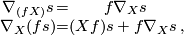
where  is a smooth function and
is a smooth function and  a vector field on
a vector field on  and
and  a section of
a section of  , and where
, and where 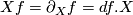 is the ordinary derivative of the function
is the ordinary derivative of the function  in the direction of
in the direction of  . By these properties,
. By these properties,  is defined locally and even pointwise regarding the first argument: For any
is defined locally and even pointwise regarding the first argument: For any 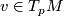 we may define
we may define 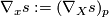 where
where  is any (local) vector field with
is any (local) vector field with 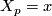 .
.
3 Curvature
A covariant derivative has all properties of the ordinary directional derivative for functions with exception of the commutativity: For functions  we have
we have 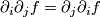 with
with
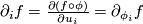 , where
, where 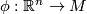 is a local diffeomorphism (local parametrization of
is a local diffeomorphism (local parametrization of  ) and
) and 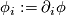 its
its  -th partial derivative. Instead, for covariant derivatives
-th partial derivative. Instead, for covariant derivatives 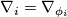 of a section
of a section  on a vector bundle
on a vector bundle  , the quantity
, the quantity
![R_{ij}s := [\nabla_i,\nabla_j]s = \nabla_i\nabla_js - \nabla_j\nabla_is](/images/math/e/0/7/e07385894231745e1b0b4fbb9cb41373.png)
is in general nonzero but just a tensor (rather than a differential operator):
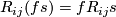 . For arbitrary vector fields
. For arbitrary vector fields 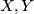 with
with
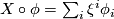 and
and 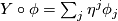 we put
we put
![R(X,Y)s = \sum_{ij} \xi^i\eta^j R_{ij}s = [\nabla_X,\nabla_Y]s - \nabla_{[X,Y]}s](/images/math/a/d/2/ad2e427e6cc5cd8d760f3ac414e3e33e.png)
where ![[X,Y] = \sum_i \left((X\eta^i) - (Y\xi^i)\right)\phi_i](/images/math/a/7/9/a79d8229e34ed9a0c225c5f9b494777e.png) denotes the Lie bracket of vector fields.
denotes the Lie bracket of vector fields.
4 Moving frames
A moving frame on  is an
is an  -tuple of sections
-tuple of sections 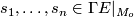 on some open subset
on some open subset 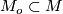 such that for any
such that for any 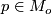 the vectors
the vectors 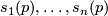 form a basis of
form a basis of 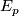 . Denoting by
. Denoting by 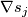 the linear map
the linear map 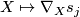 , we have
, we have
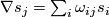
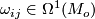 called (local) connection forms. Differentiating a second time we have
called (local) connection forms. Differentiating a second time we have 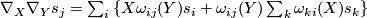 and therefore (interchanging the roles of the indices
and therefore (interchanging the roles of the indices  and
and  in the second term)
in the second term) 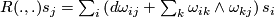
where we have used ![d\omega(X,Y) = X\omega(Y) - Y\omega(X) - \omega([X,Y])](/images/math/0/f/6/0f6e4b07f58dcae36d998c4952dda3bd.png) and
and
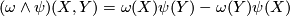 for arbitrary 1-forms
for arbitrary 1-forms 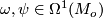 . On the other hand we let
. On the other hand we let
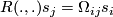
for some 2-forms 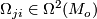 called (local) curvature forms, and thus we obtain the following relation between connection and curvature forms:
called (local) curvature forms, and thus we obtain the following relation between connection and curvature forms:
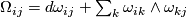
called Cartan Structure equations. Using matrix notation 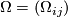 ,
, 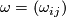 , we may write the latter equation in the short form
, we may write the latter equation in the short form
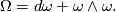
5 Parallelity and connection
A section  defined along an injective smooth curve
defined along an injective smooth curve 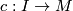 is called parallel if
is called parallel if 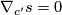 . This is a linear ODE for
. This is a linear ODE for  which is solvable along
which is solvable along  with arbitrary initial values. If
with arbitrary initial values. If 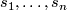 is a basis of parallel sections and
is a basis of parallel sections and 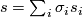 is an arbitrary section along
is an arbitrary section along  , then
, then 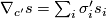 . Thus a covariant derivative is determined by its notion of parallelity and vice versa. Parallelity is given by a distribution
. Thus a covariant derivative is determined by its notion of parallelity and vice versa. Parallelity is given by a distribution 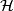 on
on  , i.e.\ a subbundle
, i.e.\ a subbundle 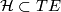 , where
, where 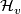 for
for 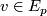 consists of the initial vectors
consists of the initial vectors 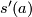 of parallel sections
of parallel sections  with
with 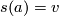 along curves
along curves ![c : [a,b] \to M](/images/math/c/4/1/c417e21a61341e002151e2c4f75792f6.png) starting at
starting at 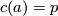 . Stated differently,
. Stated differently, 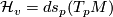 where
where  is a local section defined near
is a local section defined near  such that
such that 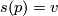 and
and 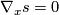 for all
for all 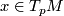 . Vice versa, a section
. Vice versa, a section  along any curve
along any curve  (a smooth map
(a smooth map 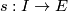 with
with 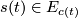 for all
for all 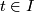 ) is parallel iff
) is parallel iff 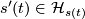 for all
for all 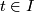 . Since this distribution "connects" the distinct fibres of
. Since this distribution "connects" the distinct fibres of  among each other, it is called a "connection".
among each other, it is called a "connection".
For any piecewise smooth curve ![c : [a,b] \to M](/images/math/c/4/1/c417e21a61341e002151e2c4f75792f6.png) from
from  to
to  and any initial value
and any initial value 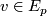 we have a parallel section
we have a parallel section  along
along  with
with 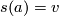 . The mapping
. The mapping 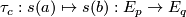 is an invertible linear map called parallel transport along the curve
is an invertible linear map called parallel transport along the curve  . In general, parallel transport depends on the curve
. In general, parallel transport depends on the curve  itself, not only on the end points
itself, not only on the end points 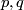 , but it is independent of the parametrization of
, but it is independent of the parametrization of  . This dependence is measured by the holonomy group
. This dependence is measured by the holonomy group 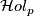 at
at  which is the set of parallel transports
which is the set of parallel transports 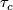 along all loops
along all loops  at
at  , i.e.piecewise smooth curves
, i.e.piecewise smooth curves
![c : [a,b] \to M](/images/math/c/4/1/c417e21a61341e002151e2c4f75792f6.png) with
with 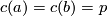 . It is known by the Ambrose-Singer theorem [Kobayashi&Nomizu1963, Theorem 8.1] that the connected component of
. It is known by the Ambrose-Singer theorem [Kobayashi&Nomizu1963, Theorem 8.1] that the connected component of 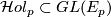 is a Lie subgroup and its Lie algebra is spanned by the linear maps
is a Lie subgroup and its Lie algebra is spanned by the linear maps 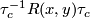 for all curves
for all curves ![c : [a,b] \to M](/images/math/c/4/1/c417e21a61341e002151e2c4f75792f6.png) starting from
starting from  and all
and all 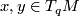 where
where 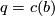 .
.
6 Connection on the frame bundle
Since it is useful to work with frames instead of single sections, we may replace  with the linear frame bundle
with the linear frame bundle 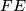 whose fibre
whose fibre 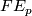 over
over 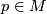 is the set of all frames (bases) of the vector space
is the set of all frames (bases) of the vector space 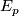 . Then parallelity of a frame
. Then parallelity of a frame 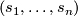 , i.e. parallelity of all sections
, i.e. parallelity of all sections 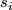 in this frame, is expressed by a distribution on
in this frame, is expressed by a distribution on 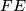 which is also called
which is also called 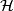 . Together with the the "vertical space"
. Together with the the "vertical space" 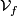 , the tangent space
, the tangent space 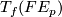 of the fibre through
of the fibre through  , it yields a direct decomposition
, it yields a direct decomposition 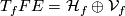 and hence we have projections
and hence we have projections 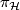 and
and 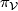 of
of 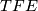 onto the two subbundles.
onto the two subbundles. 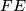 is a principal fibre bundle for the group
is a principal fibre bundle for the group 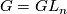 , i.e.the fibres are the orbits of a free action of
, i.e.the fibres are the orbits of a free action of  from the right given by
from the right given by 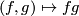 where
where 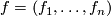 is a frame and
is a frame and 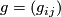 a matrix and where
a matrix and where 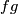 is the line with
is the line with  -th component
-th component 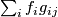 . Fixing
. Fixing 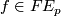 , the action
, the action 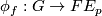 ,
, 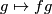 is a diffeomorphism which is equivariant with respect to right translation, and the left invariant vector fields on
is a diffeomorphism which is equivariant with respect to right translation, and the left invariant vector fields on  are turned by
are turned by 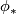 into vector fields on
into vector fields on 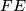 tangent to the fibres, so called fundamental vector fields. In particular, the vertical space
tangent to the fibres, so called fundamental vector fields. In particular, the vertical space 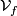 is canonically isomorphic to the Lie algebra
is canonically isomorphic to the Lie algebra 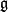 of
of  , via the infinitesimal action
, via the infinitesimal action 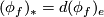 . Using this identification, the projection
. Using this identification, the projection 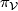 is a linear form on
is a linear form on 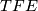 with values in
with values in 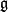 ; it will be called (global) connection form
; it will be called (global) connection form  . The form
. The form  in Section 4 will be better called
in Section 4 will be better called 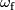 since it depends on a moving frame
since it depends on a moving frame 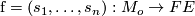 . We have
. We have
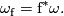
7 Curvature on the frame bundle
We get the same Cartan structure equations as in Section 4
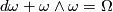
where the (global) curvature form 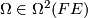 is given by
is given by
![\Omega(U,V) = -\omega([\pi_{\mathcal{H}}U,\pi_{\mathcal{H}}V])](/images/math/9/8/2/98258f9b264db5b0a57b13da382d861b.png)
for all vector fields 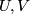 on
on 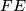 . To prove (10) we work with two special kinds of vector fields on
. To prove (10) we work with two special kinds of vector fields on 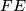 , the fundamental vertical fields
, the fundamental vertical fields 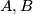 etc. which are of type
etc. which are of type 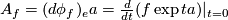 for some
for some 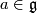 , and the horizontal lifts
, and the horizontal lifts 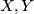 etc. which are horizontal vector fields projecting to a constant tangent vector on
etc. which are horizontal vector fields projecting to a constant tangent vector on  along every fibre; they are
along every fibre; they are  -related to a vector field
-related to a vector field 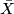 on
on  . Choosing
. Choosing 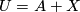 and similarly
and similarly 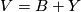 , we have
, we have 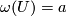 and
and 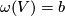 and hence
and hence 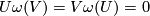 since
since 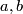 are constant elements of
are constant elements of 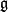 . What remains is
. What remains is
![\displaystyle -d\omega(U,V) = \omega([U,V]) = \omega([A,B] + [X,Y]) = [a,b] + \omega([X,Y])= [\omega(U),\omega(V)] - \Omega(U,V),](/images/math/c/d/c/cdcfe6576c60b20afffa50bc22dbb7cf.png)
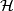 is integrable
is integrable 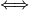
![[X,Y]](/images/math/e/1/9/e1921829b3d333bdf8227e9d46cb530b.png) is horizontal
is horizontal 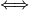
![\Omega(X,Y) = -\omega([X,Y]) = 0](/images/math/1/c/8/1c8e1719c916e83f55bbc6f7c874e033.png) .
.
8 Connections on general principal bundles
More generally, let  be a
be a  -principal bundle over
-principal bundle over  : A manifold
: A manifold  with a smooth submersion
with a smooth submersion 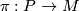 and a free action of a Lie group
and a free action of a Lie group  on
on  from the right such that the orbits are precisely the fibres, the preimages
from the right such that the orbits are precisely the fibres, the preimages 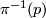 ,
, 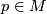 . A connection on
. A connection on  is a
is a  -invariant distribution
-invariant distribution 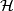 on
on  (also called the "horizontal distribution") which is complementary to the tangent spaces of the fibres forming the "vertical distribution"
(also called the "horizontal distribution") which is complementary to the tangent spaces of the fibres forming the "vertical distribution" 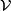 . As before, each vertical space can be identified with the Lie algebra
. As before, each vertical space can be identified with the Lie algebra 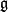 of
of  , and thus the vertical projection
, and thus the vertical projection 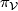 can be viewed as a
can be viewed as a 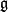 -valued 1-form
-valued 1-form 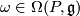 , and the equations (10) and (11) hold accordingly. If
, and the equations (10) and (11) hold accordingly. If 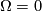 , then
, then  splits geometrically as
splits geometrically as 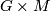 at least locally, and (10) becomes the Maurer-Cartan equation of the Lie group
at least locally, and (10) becomes the Maurer-Cartan equation of the Lie group  . For any smooth action
. For any smooth action
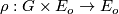 of
of  on a smooth manifold
on a smooth manifold 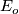 we consider the associated bundle
we consider the associated bundle 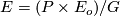 where the action on
where the action on 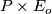 is given by
is given by 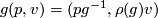 . This is a bundle over
. This is a bundle over  with fibre
with fibre 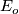 , and since the distribution
, and since the distribution 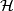 is
is  -invariant, it can be transferred to
-invariant, it can be transferred to  via
via 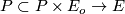 , defining a connection on
, defining a connection on  . In the case
. In the case 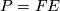 for a vector bundle
for a vector bundle  and
and 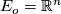 with its linear
with its linear 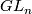 -action we have
-action we have 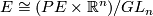 , using the map
, using the map 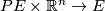 ,
, 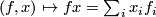 . This map is obviously invariant under the diagonal
. This map is obviously invariant under the diagonal 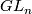 -action on
-action on 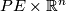 since
since 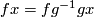 ; it is the usual identification of
; it is the usual identification of 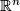 with the vector space
with the vector space 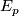 by means of the basis
by means of the basis 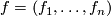 .
.
9 Connections on the tangent bundle
The tangent bundle 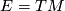 is somewhat special since it carries another 1-form
is somewhat special since it carries another 1-form 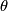 besides
besides  . In the moving frame language where a local frame
. In the moving frame language where a local frame 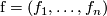 of
of  is given on an open subset
is given on an open subset 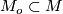 , any vector field
, any vector field  can be written as
can be written as 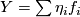 . The coefficients
. The coefficients 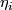 depend linearly on
depend linearly on  , and we may write
, and we may write 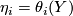 where the 1-forms
where the 1-forms 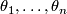 om
om 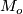 form the dual basis of
form the dual basis of 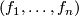 , i.e.
, i.e. 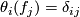 . Thus
. Thus
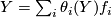
If we have a covariant derivative  on
on  and another vector field
and another vector field  , we obtain
, we obtain
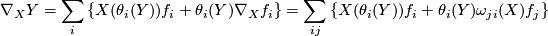
from which we derive (interchanging the roles of  and
and  in the second term)
in the second term)
![\displaystyle T(X,Y): = \nabla_XY-\nabla_YX - [X,Y] = \sum_{ij}\left(d\theta_i + \omega_{ij}\wedge\theta_j\right)(X,Y)f_i.](/images/math/9/e/8/9e8fd6b52be12df9fc8a2d3af87c04b1.png)
This tensor 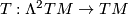 is called Torsion tensor; letting
is called Torsion tensor; letting
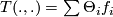
for some 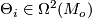 and putting
and putting
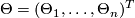 (called torsion form) and
(called torsion form) and
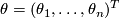 (sometimes called soldering form), we end up with the second Cartan structure equation
(sometimes called soldering form), we end up with the second Cartan structure equation
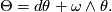
The following section explains why beneath (11) a second equation occurs for  .
.
10 Affine connections
An affine frame on 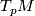 is a pair
is a pair 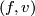 where
where 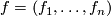 is a frame of
is a frame of 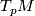 and
and 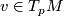 . This is acted on from the right by the affine group
. This is acted on from the right by the affine group 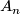 which consists of the inhomogeneous linear transformations
which consists of the inhomogeneous linear transformations 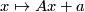 on
on 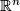 with
with 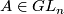 and
and 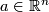 : we let
: we let
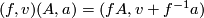
where the frame  is considered as the isomorphism
is considered as the isomorphism 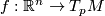 mapping the standard basis vector
mapping the standard basis vector 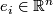 onto
onto 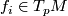 . This action turns the set
. This action turns the set 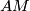 of affine frames on
of affine frames on  into a
into a 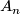 -principal bundle. A connection on the
-principal bundle. A connection on the 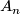 -principal bundle
-principal bundle 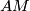 will be called generalized affine connection. Its connection and curvature forms
will be called generalized affine connection. Its connection and curvature forms 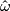 ,
, 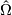 are
are 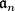 -valued where
-valued where 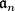 is the Lie algebra of
is the Lie algebra of 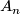 . Since
. Since 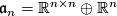 , the forms split accordingly into a matrix and a vector component. Now we consider the embedding
, the forms split accordingly into a matrix and a vector component. Now we consider the embedding 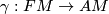 with
with 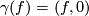 . For the pull back forms on
. For the pull back forms on 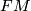 we have the same splitting:
we have the same splitting:
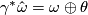
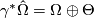
where the first term on the right takes values in 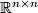 , the second on in
, the second on in
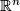 . Moreover, the Cartan structure equations for the affine group are
. Moreover, the Cartan structure equations for the affine group are
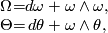
using agian the splitting 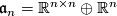 . If
. If
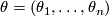 has the special property (12), we call the connection affine, and
has the special property (12), we call the connection affine, and 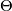 equals the torsion form as introduced in the last section.
equals the torsion form as introduced in the last section.
11 References
- [Kobayashi&Nomizu1963] S. Kobayashi and K. Nomizu, Foundations of differential geometry. Vol I, Interscience Publishers, a division of John Wiley & Sons, New York-London, 1963. MR1393940 (97c:53001a) Zbl 0508.53002
12 External links
- The Encylopedia of Mathematics article on connections
- The Wikipedia page about connections