Complex bordism
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 09:39, 1 April 2011 and the changes since publication. |
Contents |
1 Introduction
Complex bordism (also known as unitary bordism) is the bordism theory of stably complex manifolds. It is one of the most important theories of bordism with additional structure, or B-bordism.
The theory of complex bordism is much richer than its unoriented analogue, and at the same time is not as complicated as oriented bordism or other bordism theories with additional structure (B-bordism). Thanks to this, the complex cobordism theory has found the most striking and important applications in algebraic topology and beyond. Many of these applications, including the formal group techniques and Adams-Novikov spectral sequence were outlined in the pioneering work [Novikov1967].
2 Stably complex structures
A direct attempt to define the
bordism relation on complex manifolds fails because the manifold
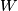 is odd-dimensional and therefore cannot be complex. In order to work with complex manifolds in the bordism theory, one needs to weaken the notion of a complex structure. This leads directly to considering stably complex (also known as
weakly almost complex, stably almost complex or quasicomplex) manifolds.
is odd-dimensional and therefore cannot be complex. In order to work with complex manifolds in the bordism theory, one needs to weaken the notion of a complex structure. This leads directly to considering stably complex (also known as
weakly almost complex, stably almost complex or quasicomplex) manifolds.
Let 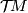 denote the tangent bundle of
denote the tangent bundle of  , and
, and 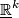 the product vector bundle
the product vector bundle 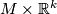 over
over  . A tangential stably complex structure on
. A tangential stably complex structure on  is
determined by a choice of an isomorphism
is
determined by a choice of an isomorphism
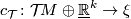
between the "stable" tangent bundle and a complex vector
bundle  over
over  . Some of the choices of such isomorphisms
are deemed to be equivalent, i.e. determining the same stably
complex structures (see details in Chapters II and VII of [Stong1968]). In
particular, two stably complex structures are equivalent if they
differ by a trivial complex summand. A normal stably complex structure on
. Some of the choices of such isomorphisms
are deemed to be equivalent, i.e. determining the same stably
complex structures (see details in Chapters II and VII of [Stong1968]). In
particular, two stably complex structures are equivalent if they
differ by a trivial complex summand. A normal stably complex structure on  is determined by a choice of a complex bundle
structure on the normal bundle
is determined by a choice of a complex bundle
structure on the normal bundle 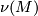 of an embedding
of an embedding
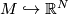 . Tangential and normal stably
complex structures on
. Tangential and normal stably
complex structures on  determine each other by means of the
canonical isomorphism
determine each other by means of the
canonical isomorphism 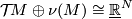 . We therefore may restrict
our attention to tangential structures only.
. We therefore may restrict
our attention to tangential structures only.
A stably complex manifold is a pair 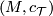 consisting of a manifold
consisting of a manifold  and a stably complex structure
and a stably complex structure
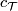 on it. This is a generalisation of a complex and
almost complex manifold (where the latter means a manifold
with a choice of a complex structure on
on it. This is a generalisation of a complex and
almost complex manifold (where the latter means a manifold
with a choice of a complex structure on 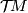 , i.e. a
stably complex structure
, i.e. a
stably complex structure 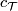 with
with  ).
).
Example 2.1.
Let 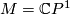 . The standard complex structure on
. The standard complex structure on  is
equivalent to a stably complex structure determined by the
isomorphism
is
equivalent to a stably complex structure determined by the
isomorphism
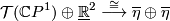
where 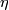 is the Hopf line bundle. On the other hand, the
isomorphism
is the Hopf line bundle. On the other hand, the
isomorphism
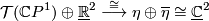
determines a trivial stably complex structure on 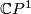 .
.
3 Definition of bordism and cobordism
The bordism relation can be defined between stably complex
manifolds. Like the case of unoriented bordism, the set of
bordism classes ![[M,c_{\mathcal T}]](/images/math/b/2/f/b2fc6d73eb430a4b0c96071988365163.png) of stably complex manifolds of dimension
of stably complex manifolds of dimension  is an Abelian group with respect to the disjoint union. This group
is called the
is an Abelian group with respect to the disjoint union. This group
is called the  -dimensional complex bordism group and
denoted
-dimensional complex bordism group and
denoted 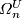 . The zero element is represented by the bordism
class of any manifold
. The zero element is represented by the bordism
class of any manifold  which bounds and whose stable tangent
bundle is trivial (and therefore isomorphic to a product complex
vector bundle
which bounds and whose stable tangent
bundle is trivial (and therefore isomorphic to a product complex
vector bundle 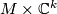 ). The sphere
). The sphere  provides an example
of such a manifold. The opposite element to the bordism class
provides an example
of such a manifold. The opposite element to the bordism class
![[M,c_{\mathcal T}]](/images/math/b/2/f/b2fc6d73eb430a4b0c96071988365163.png) in the group
in the group 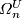 may be
represented by the same manifold
may be
represented by the same manifold  with the stably complex
structure determined by the isomorphism
with the stably complex
structure determined by the isomorphism
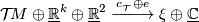
where 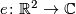 is given by
is given by 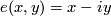 .
.
An abbreviated notation ![[M]](/images/math/f/a/0/fa08c3d5d2f54260952acc8a646b5025.png) for the complex
bordism class will be used whenever the stably complex structure
for the complex
bordism class will be used whenever the stably complex structure 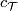 is clear from the context.
is clear from the context.
The complex bordism group 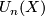 and cobordism group
and cobordism group 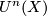 of a space
of a space  may also be defined
geometrically, at least for the case when
may also be defined
geometrically, at least for the case when  is a manifold. This can be done along the lines suggested by [Quillen1971a] and [Dold1978] by considering special "stably complex" maps
of manifolds
is a manifold. This can be done along the lines suggested by [Quillen1971a] and [Dold1978] by considering special "stably complex" maps
of manifolds  to
to  . However, nowadays the homotopical approach to
bordism has taken over, and the (co)bordism groups are usually
defined using the Pontrjagin-Thom construction similarly to the unoriented case:
. However, nowadays the homotopical approach to
bordism has taken over, and the (co)bordism groups are usually
defined using the Pontrjagin-Thom construction similarly to the unoriented case:
![\displaystyle \begin{aligned} U_n(X)&=\lim_{k\to\infty}\pi_{2k+n}((X_+)\wedge MU(k)),\\ U^n(X)&=\lim_{k\to\infty}[\Sigma^{2k-n}(X_+),MU(k)] \end{aligned}](/images/math/3/8/8/388203cfec203d491a8ba0f9062a963f.png)
where 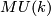 is the Thom space of the universal complex
is the Thom space of the universal complex  -plane
bundle
-plane
bundle 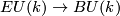 , and
, and ![[X,Y]](/images/math/e/1/9/e1921829b3d333bdf8227e9d46cb530b.png) denotes the set of homotopy classes of pointed maps
from
denotes the set of homotopy classes of pointed maps
from  to
to  . These groups are
. These groups are 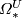 -modules
and give rise to a multiplicative (co)homology theory. In
particular,
-modules
and give rise to a multiplicative (co)homology theory. In
particular, 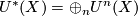 is a graded ring.
is a graded ring.
The graded
ring 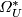 with
with 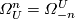 is
called the complex cobordism ring; it has nontrivial
elements only in nonpositively graded components.
is
called the complex cobordism ring; it has nontrivial
elements only in nonpositively graded components.
4 Geometric cobordisms
There is one important case when certain cobordism classes can be represented very explicitly by maps of manifolds.
For any cell complex  the cohomology group
the cohomology group 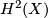 can be identified with the set
can be identified with the set ![[X,\mathbb C P^\infty]](/images/math/2/3/f/23f1ff840ec28653072a02740f623e5a.png) of homotopy classes of maps into
of homotopy classes of maps into 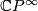 . Since
. Since 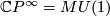 , every element
, every element 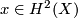 also determines
a cobordism class
also determines
a cobordism class 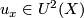 . The elements of
. The elements of 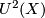 obtained in this way are called geometric cobordisms
of
obtained in this way are called geometric cobordisms
of  . We therefore may view
. We therefore may view 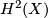 as a subset in
as a subset in 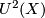 , however the group operation in
, however the group operation in 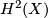 is not obtained by
restricting the group operation in
is not obtained by
restricting the group operation in 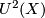 (see Formal group laws and genera for the relationship
between the two operations).
(see Formal group laws and genera for the relationship
between the two operations).
When  is a manifold, geometric cobordisms may be described by
submanifolds
is a manifold, geometric cobordisms may be described by
submanifolds  of codimension 2 with a fixed complex
structure on the normal bundle.
of codimension 2 with a fixed complex
structure on the normal bundle.
Indeed, every 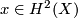 corresponds to a homotopy class of
maps
corresponds to a homotopy class of
maps 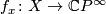 . The image
. The image 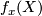 is contained
in some
is contained
in some 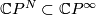 , and we may assume that
, and we may assume that
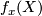 is transverse to a certain hyperplane
is transverse to a certain hyperplane 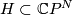 .
Then
.
Then 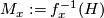 is a codimension 2 submanifold in
is a codimension 2 submanifold in  whose normal bundle acquires a complex structure by restriction of
the complex structure on the normal bundle of
whose normal bundle acquires a complex structure by restriction of
the complex structure on the normal bundle of 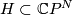 .
Changing the map
.
Changing the map 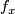 within its homotopy class does not affect
the bordism class of the embedding
within its homotopy class does not affect
the bordism class of the embedding 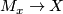 .
.
Conversely, assume given a submanifold  of codimension
2 whose normal bundle is endowed with a complex structure. Then
the composition
of codimension
2 whose normal bundle is endowed with a complex structure. Then
the composition
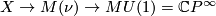
of the Pontrjagin-Thom collapse map 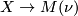 and the map of
Thom spaces corresponding to the classifying map
and the map of
Thom spaces corresponding to the classifying map 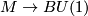 of
of  defines an element
defines an element 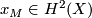 , and therefore a
geometric cobordism.
, and therefore a
geometric cobordism.
If  is an oriented manifold, then a choice of complex structure
on the normal bundle of a codimension 2 embedding
is an oriented manifold, then a choice of complex structure
on the normal bundle of a codimension 2 embedding  is
equivalent to orienting
is
equivalent to orienting  . The image of the fundamental class of
. The image of the fundamental class of
 in the homology of
in the homology of  is Poincaré dual to
is Poincaré dual to 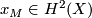 .
.
5 Structure results
The complex bordism ring 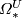 is described as follows.
is described as follows.
Theorem 5.1.
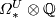 is a polynomial ring over
is a polynomial ring over 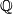 generated by the bordism classes of complex projective spaces
generated by the bordism classes of complex projective spaces 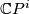 ,
, 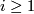 .
.
- Two stably complex manifolds are bordant if and only if they have identical sets of Chern characteristic numbers.
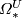 is a polynomial ring over
is a polynomial ring over  with one generator
with one generator 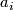 in every even dimension
in every even dimension 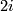 , where
, where 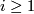 .
.
Part 1 can be proved by the methods of [Thom1954]. Part 2 follows from the results of [Milnor1960] and [Novikov1960]. Part 3 is the most difficult one; it was done by [Novikov1960] using the Adams spectral sequence and structure theory of Hopf algebras (see also [Novikov1962] for a more detailed account) and Milnor (unpublished, but see [Thom1995]) in 1960. Another more geometric proof was given by [Stong1965], see also [Stong1968].
6 Multiplicative generators
6.1 Preliminaries: characteristic numbers detecting generators
To describe a set of multiplicative generators for the ring
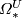 we shall need a special characteristic class of
complex vector bundles. Let
we shall need a special characteristic class of
complex vector bundles. Let  be a complex
be a complex  -plane bundle
over a manifold
-plane bundle
over a manifold  . Write its total Chern class formally as
follows:
. Write its total Chern class formally as
follows:
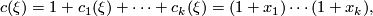
so that 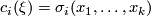 is the
is the  th
elementary symmetric function in formal indeterminates. These
indeterminates acquire a geometric meaning if
th
elementary symmetric function in formal indeterminates. These
indeterminates acquire a geometric meaning if  is a sum
is a sum
 of line bundles; then
of line bundles; then
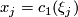 ,
, 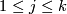 . Consider the polynomial
. Consider the polynomial
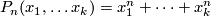
and express it via the elementary symmetric functions:
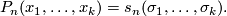
Substituting the Chern classes for the elementary symmetric
functions we obtain a certain characteristic class of  :
:
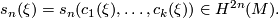
This characteristic class plays an important role in detecting the polynomial generators of the complex bordism ring, because of the following properties (which follow immediately from the definition).
Proposition 6.1.
-
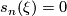 for
for 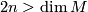 .
.
-
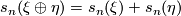 .
.
Given a stably complex manifold 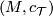 of
dimension
of
dimension  , define its characteristic number
, define its characteristic number
![\displaystyle s_n[M]=s_n(\xi)\langle M\rangle\in\mathbb Z](/images/math/8/9/c/89c6094854b72cf3c246560dbf4a5426.png)
where  is the complex bundle from the definition of stably complex structure, and
is the complex bundle from the definition of stably complex structure, and 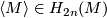 the fundamental homology class.
the fundamental homology class.
Corollary 6.2.
If a bordism class ![[M]\in\varOmega_{2n}^U](/images/math/1/b/3/1b39e948a62e5b7b14435537d9065eb5.png) decomposes as
decomposes as
![[M_1]\times[M_2]](/images/math/5/3/c/53cd9b71dc8c7bb597dbe56ad4be2788.png) where
where 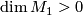 and
and 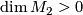 , then
, then
![s_n[M]=0](/images/math/0/c/1/0c12347761299dda297564bb7370acaf.png) .
.
It follows that the characteristic number 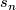 vanishes on
decomposable elements of
vanishes on
decomposable elements of 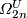 . It also detects indecomposables that may be chosen as polynomial
generators. In
fact, the following result is a byproduct of the calculation of
. It also detects indecomposables that may be chosen as polynomial
generators. In
fact, the following result is a byproduct of the calculation of 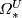 :
:
Theorem 6.3.
A bordism class ![[M]\in\varOmega_{2n}^U](/images/math/1/b/3/1b39e948a62e5b7b14435537d9065eb5.png) may be chosen as a
polynomial generator
may be chosen as a
polynomial generator 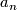 of the ring
of the ring 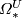 if and only
if
if and only
if
![\displaystyle s_n[M]=\begin{cases} \pm1, &\text{if $n\ne p^k-1$ for any prime $p$;}\\ \pm p, &\text{if $n=p^k-1$ for some prime $p$.} \end{cases}](/images/math/c/8/5/c85430ad17dca6960d6989d8d71d9c5d.png)
(Ed Floyd was fond of
calling the characteristic numbers ![s_n[M]](/images/math/9/9/7/997cfacfcd870d214fb63420b9765762.png) the "magic numbers" of manifolds.)
the "magic numbers" of manifolds.)
6.2 Milnor hypersurfaces
A universal description of connected manifolds representing the
polynomial generators 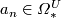 is unknown. Still,
there is a particularly nice family of manifolds whose bordism
classes generate the whole ring
is unknown. Still,
there is a particularly nice family of manifolds whose bordism
classes generate the whole ring 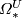 . This
family is redundant though, so there are algebraic relations between
their bordism classes.
. This
family is redundant though, so there are algebraic relations between
their bordism classes.
Fix a pair of integers 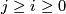 and consider the product
and consider the product 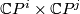 . Its algebraic subvariety
. Its algebraic subvariety
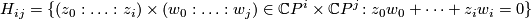
is called a Milnor hypersurface. Note that 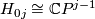 .
.
The Milnor hypersurface 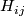 may be identified with the set of pairs
may be identified with the set of pairs 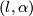 , where
, where  is a line in
is a line in 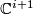 and
and
 is a hyperplane in
is a hyperplane in 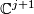 containing
containing  . The projection
. The projection 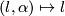 describes
describes 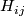 as the total space of a bundle over
as the total space of a bundle over 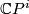 with fibre
with fibre 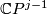 .
.
Denote by 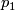 and
and  the projections of
the projections of 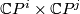 onto the first and second factors respectively, and by
onto the first and second factors respectively, and by 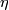 the
Hopf line bundle over a complex projective space; then
the
Hopf line bundle over a complex projective space; then 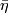 is the hyperplane section
bundle. We have
is the hyperplane section
bundle. We have
![\displaystyle H^*(\mathbb C P^i\times\mathbb C P^j)=\mathbb Z[x,y]/(x^{i+1}=0,\;y^{j+1}=0)](/images/math/5/a/6/5a67f0af059ef2437ca32f0cc4ed98bf.png)
where 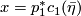 ,
, 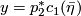 .
.
Proposition 6.4.
The geometric cobordism in 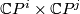 corresponding to
the element
corresponding to
the element 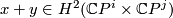 is represented by the
submanifold
is represented by the
submanifold 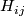 . In particular, the image of the fundamental
class
. In particular, the image of the fundamental
class 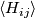 in
in 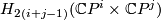 is Poincaré dual to
is Poincaré dual to 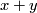 .
.
See the proof here (opens a separate pdf).
Lemma 6.5. We have
![\displaystyle s_{i+j-1}[H_{ij}]=\begin{cases} j,&\text{if \ $i=0$, i.e. $H_{ij}=\mathbb C P^{j-1}$};\\ 2,&\text{if \ $i=j=1$};\\ 0,&\text{if \ $i=1$, $j>1$};\\ -\binom{i+j}i,&\text{if \ $i>1$}. \end{cases}](/images/math/3/d/2/3d25a19b1a59aff9251fd5cc03455c4e.png)
See the proof here (opens a separate pdf).
Theorem 6.6.
The bordism classes ![\{[H_{ij}],\;0\le i\le j\}](/images/math/6/0/2/602e58588f6569c810c8906ac5772fb3.png) multiplicatively
generate the complex bordism ring
multiplicatively
generate the complex bordism ring 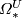 .
.
Proof. This follows from the fact that
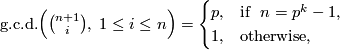
and the previous Lemma.
Example 6.7.
-
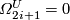 ;
;
-
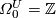 , generated by a point;
, generated by a point;
-
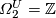 , generated by
, generated by ![[\mathbb CP^1]](/images/math/d/9/8/d9808cc75969c640dd27b12613e7e118.png) , as
, as 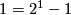 and
and ![s_1[\mathbb C P^1]=2](/images/math/b/1/6/b16012ec57f630fc5ca86186abf2a073.png) ;
;
-
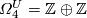 , generated by
, generated by ![[\mathbb CP^1\times\mathbb CP^1]](/images/math/8/e/0/8e09f2e4275f4f5ab41944df28a4782d.png) and
and ![[\mathbb CP^2]](/images/math/9/9/c/99ca2dea5de9826c5bb376a2b308482a.png) , as
, as 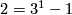 and
and ![s_2[\mathbb C P^2]=3](/images/math/2/e/3/2e3d029e2b0fc5946ad2fe1e5e7deb9d.png) ;
;
-
![[\mathbb C P^3]](/images/math/6/4/1/64191ba5261086e42c4492940f4c2141.png) cannot be taken as the polynomial generator
cannot be taken as the polynomial generator 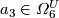 , since
, since ![s_3[\mathbb C P^3]=4](/images/math/8/a/5/8a5c36e6ead9ec0e8a1f7f824e3b2344.png) , while
, while 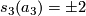 . The bordism class
. The bordism class ![[H_{22}]+[\mathbb C P^3]](/images/math/9/9/4/9949e69f6d00493a888170da4240f1c3.png) may be taken as
may be taken as 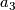 .
.
The previous theorem about the multiplicative generators for 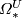 has the following important addendum.
has the following important addendum.
Theorem 6.8 (Milnor).
Every bordism class 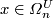 with
with 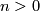 contains a
nonsingular algebraic variety (not necessarily connected).
contains a
nonsingular algebraic variety (not necessarily connected).
(The Milnor hypersufaces are algebraic, but one also needs to represent ![-[H_{ij}]](/images/math/4/5/1/451391403c803841b154e367c8a4b130.png) by algebraic varieties!)
For the proof see Chapter 7 of [Stong1968].
by algebraic varieties!)
For the proof see Chapter 7 of [Stong1968].
The following question is still open, even in complex dimension 2.
Problem 6.9 (Hirzebruch).
Describe the set of bordism classes in
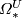 containing connected nonsingular algebraic
varieties.
containing connected nonsingular algebraic
varieties.
Example 6.10.
Every class ![k[\mathbb C P^1]\in\varOmega^U_2](/images/math/2/f/5/2f55b4741af83210aeb2383e02fbffc9.png) contains a nonsingular algebraic
variety, namely, a disjoint union of
contains a nonsingular algebraic
variety, namely, a disjoint union of  copies of
copies of 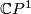 for
for
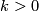 and a Riemannian surface of genus
and a Riemannian surface of genus 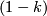 for
for 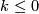 .
Connected algebraic varieties are only contained in the bordism
classes
.
Connected algebraic varieties are only contained in the bordism
classes ![k[\mathbb C P^1]](/images/math/a/4/8/a4858f1ae38fdf4f07fab2f7fc1493ad.png) with
with 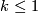 .
.
6.3 Toric generators and quasitoric representatives in cobordism classes
There is an alternative set of multiplicative generators ![\{[B_{ij}],0\le i\le j\}](/images/math/d/a/6/da61afd32b49744916a2a39d7fd5684e.png) for the complex bordism ring
for the complex bordism ring 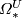 , consisting of nonsingular projective toric varieties, or toric manifolds. Every
, consisting of nonsingular projective toric varieties, or toric manifolds. Every 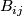 therefore supports an effective action of a ``big torus" (of dimension half the dimension of the manifold) with isolated fixed points. The construction of
therefore supports an effective action of a ``big torus" (of dimension half the dimension of the manifold) with isolated fixed points. The construction of 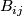 is due to [Buchstaber&Ray2001] (see also [Buchstaber&Panov2002] and [Buchstaber&Panov&Ray2007]).
is due to [Buchstaber&Ray2001] (see also [Buchstaber&Panov2002] and [Buchstaber&Panov&Ray2007]).
Milnor hypersurfaces 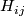 are not toric manifolds for
are not toric manifolds for  , because of a simple cohomological obstruction (see Proposition 5.43 in [Buchstaber&Panov2002]).
, because of a simple cohomological obstruction (see Proposition 5.43 in [Buchstaber&Panov2002]).
The manifold 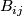 is constructed as a projectivisation of a sum of
is constructed as a projectivisation of a sum of  line bundles over the bounded flag manifold
line bundles over the bounded flag manifold 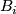 .
.
A bounded flag in 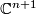 is a complete flag
is a complete flag
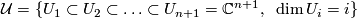
for which 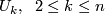 , contains the coordinate subspace
, contains the coordinate subspace 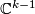 spanned by the first
spanned by the first 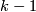 standard basis vectors.
standard basis vectors.
The set 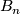 of all bounded flags in
of all bounded flags in 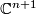 is a smooth complex algebraic variety of dimension
is a smooth complex algebraic variety of dimension  (cf. [Buchstaber&Ray2001]), referred to as the bounded flag manifold. The action of the algebraic torus
(cf. [Buchstaber&Ray2001]), referred to as the bounded flag manifold. The action of the algebraic torus 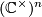 on
on 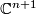 given by
given by
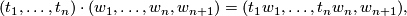
where 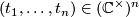 and
and
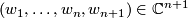 , induces an action on
bounded flags, and therefore endows
, induces an action on
bounded flags, and therefore endows 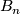 with a structure of a toric manifold.
with a structure of a toric manifold.
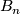 is also the total space of a Bott tower, that is, a tower of fibrations with base
is also the total space of a Bott tower, that is, a tower of fibrations with base 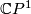 and fibres
and fibres 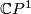 in which every stage is the projectivisation of a sum of two line bundles. In particular,
in which every stage is the projectivisation of a sum of two line bundles. In particular, 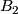 is the Hirzebruch surface
is the Hirzebruch surface 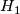 .
.
The manifold 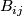 (
(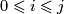 ) consists of pairs
) consists of pairs 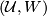 , where
, where 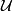 is a bounded flag in
is a bounded flag in 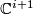 and
and  is a line in
is a line in 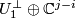 . (Here
. (Here  denotes
the orthogonal complement to
denotes
the orthogonal complement to 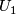 in
in 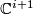 , so that
, so that
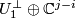 is the orthogonal complement to
is the orthogonal complement to 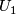 in
in 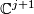 .) Therefore,
.) Therefore, 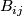 is the total space of a bundle
over
is the total space of a bundle
over 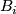 with fibre
with fibre 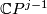 . This bundle is the
projectivisation of a sum of line bundles, which implies that
. This bundle is the
projectivisation of a sum of line bundles, which implies that 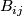 is
a complex
is
a complex 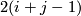 -dimensional toric manifold.
-dimensional toric manifold.
The bundle 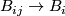 is the pullback of the bundle
is the pullback of the bundle 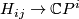 along the map
along the map 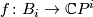 taking a bounded flag
taking a bounded flag 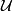 to its first line
to its first line 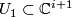 . This is described by the diagram
. This is described by the diagram
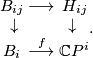
(The bundle 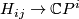 , unlike
, unlike 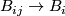 , is not a projectivisation of a sum of line bundles, which prevents the torus action on
, is not a projectivisation of a sum of line bundles, which prevents the torus action on 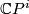 to lift to an action on the total space.)
to lift to an action on the total space.)
Lemma 6.11.
We have ![s_{i+j-1}[B_{ij}]=s_{i+j-1}[H_{ij}]](/images/math/6/9/3/693d4c4649d2d546aea818a0a80230e3.png) .
.
The proof uses the fact that the map 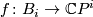 has degree one.
has degree one.
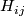 and
and 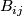 are not cobordant in general, although
are not cobordant in general, although 
Theorem 6.12 ([Buchstaber&Ray2001]).
The bordism classes of toric manifolds ![\{[B_{ij}],\;0\le i\le j\}](/images/math/8/5/5/85598185e65d290858d385121f285f4d.png) multiplicatively
generate the complex bordism ring
multiplicatively
generate the complex bordism ring 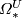 . Therefore, every complex bordism class contains a disjoint union of toric manifolds.
. Therefore, every complex bordism class contains a disjoint union of toric manifolds.
Proof. The first statement follows from the fact that the Milnor hypersurfaces generate the complex bordism ring and the previous Lemma. A product of toric manifolds is toric, but a disjoint union of toric manifolds is not a toric manifold, since toric manifolds are connected by definition.
The manifolds 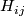 and
and 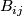 are not bordant in general, although
are not bordant in general, although 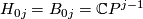 and
and 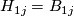 by
definition.
by
definition.
Connected representatives in cobordism classes cannot be found within toric manifolds because of severe restrictions on their characteristic numbers. (For example, the Todd genus of every toric manifold is 1.) A topological generalisation of toric manifolds was suggested in [Davis&Januszkiewicz1991a] (see also [Buchstaber&Panov2002]). These manifolds have become known as quasitoric. A quasitoric manifold is a smooth manifold of dimension  with a locally standard action of an
with a locally standard action of an  -dimensional torus whose quotient is a simple polytope. Quasitoric manifolds generally fail to be complex or even almost complex, but they always admit stably complex structures [Buchstaber&Ray2001].
-dimensional torus whose quotient is a simple polytope. Quasitoric manifolds generally fail to be complex or even almost complex, but they always admit stably complex structures [Buchstaber&Ray2001].
Theorem 6.13 ([Buchstaber&Panov&Ray2007]).
In dimensions 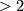 , every complex cobordism class contains a
quasitoric manifold, necessarily connected, whose stably complex
, every complex cobordism class contains a
quasitoric manifold, necessarily connected, whose stably complex
7 Adams-Novikov spectral sequence
A principal motivation for [Novikov1967] was to develop a version of the Adams spectral sequence in which mod  cohomology (and the Steenrod algebra) are replaced by complex cobordism theory (and its ring of stable cohomology operations), for the purpose of computing stable homotopy groups. The foundations for the Adams-Novikov spectral sequence were laid in this paper, and many applications and computations have followed. An introduction to the work of Novikov on complex cobordism is given in [Adams1974]. The most comprehensive study of the Adams-Novikov spectral sequence is [Ravenel1986], currently available in a second edition from AMS/Chelsea.
cohomology (and the Steenrod algebra) are replaced by complex cobordism theory (and its ring of stable cohomology operations), for the purpose of computing stable homotopy groups. The foundations for the Adams-Novikov spectral sequence were laid in this paper, and many applications and computations have followed. An introduction to the work of Novikov on complex cobordism is given in [Adams1974]. The most comprehensive study of the Adams-Novikov spectral sequence is [Ravenel1986], currently available in a second edition from AMS/Chelsea.
8 References
- [Adams1974] J. F. Adams, Stable homotopy and generalised homology, University of Chicago Press, Chicago, Ill., 1974. MR0402720 (53 #6534) Zbl 0309.55016
- [Buchstaber&Panov&Ray2007] V. M. Buchstaber, T. E. Panov and N. Ray, Spaces of polytopes and cobordism of quasitoric manifolds, Mosc. Math. J. 7 (2007), no.2, 219–242, 350. MR2337880 (2008f:55006) Zbl 1176.55004
- [Buchstaber&Panov2002] V. M. Buchstaber and T. E. Panov, Torus actions and their applications in topology and combinatorics, American Mathematical Society, 2002. MR1897064 (2003e:57039) Zbl 1012.52021
- [Buchstaber&Ray2001] V. M. Buchstaber and N. Ray, Tangential structures on toric manifolds, and connected sums of polytopes, Internat. Math. Res. Notices (2001), no.4, 193–219. MR1813798 (2002b:57043) Zbl 0996.52013
- [Davis&Januszkiewicz1991a] M. W. Davis and T. Januszkiewicz, Convex polytopes, Coxeter orbifolds and torus actions, Duke Math. J. 62 (1991), no.2, 417–451. MR1104531 (92i:52012) Zbl 0733.52006
- [Dold1978] A. Dold, Geometric cobordism and the fixed point transfer, in Algebraic topology (Proc. Conf., Univ. British Columbia, Vancouver, B.C., 1977), Lecture Notes in Math. 673, Springer, Berlin, (1978), 32–87. MR517084 (80g:57052) Zbl 0386.57005
- [Milnor1960] J. Milnor, On the cobordism ring
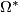 and a complex analogue. I, Amer. J. Math. 82 (1960), 505–521. MR0119209 (22 #9975) Zbl 0095.16702
and a complex analogue. I, Amer. J. Math. 82 (1960), 505–521. MR0119209 (22 #9975) Zbl 0095.16702
- [Novikov1960] S. P. Novikov, Some problems in the topology of manifolds connected with the theory of Thom spaces, Soviet Math. Dokl. 1 (1960), 717–720. MR0121815 (22 #12545) Zbl 0094.35902
- [Novikov1962] S. P. Novikov, Homotopy properties of Thom complexes, Mat. Sb. (N.S.) 57 (99) (1962), 407–442. MR0157381 (28 #615) Zbl 0193.51801
- [Novikov1967] S. P. Novikov, Methods of algebraic topology from the point of view of cobordism theory, Math. USSR, Izv. 1, (1967) 827–913. MR0221509 (36 #4561) Zbl 0176.52401
- [Quillen1971a] D. Quillen, Elementary proofs of some results of cobordism theory using Steenrod operations, Advances in Math. 7 (1971), 29–56 (1971). MR0290382 (44 #7566) Zbl 0214.50502
- [Ravenel1986] D. C. Ravenel, Complex cobordism and stable homotopy groups of spheres, Academic Press Inc., Orlando, FL, 1986. MR860042 (87j:55003) Zbl 1073.55001
- [Stong1965] R. E. Stong, Relations among characteristic numbers. I, Topology 4 (1965), 267–281. MR0192515 (33 #740) Zbl 0136.20503
- [Stong1968] R. E. Stong, Notes on cobordism theory, Princeton University Press, Princeton, N.J., 1968. MR0248858 (40 #2108) Zbl 0277.57010
- [Thom1954] R. Thom, Quelques propriétés globales des variétés différentiables, Comment. Math. Helv. 28 (1954), 17–86. MR0061823 (15,890a) Zbl 0057.15502
- [Thom1995] R. Thom, Travaux de Milnor sur le cobordisme, Séminaire Bourbaki, Vol. 5, Exp. No. 180, Soc. Math. France, Paris, (1995), 169–177. MR1603465 Zbl 0116.40402