Hirzebruch surfaces
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 09:48, 1 April 2011 and the changes since publication. |
Contents |
1 Introduction
Hirzebruch surfaces were introduced by Hirzebruch (without that name) in his thesis [Hirzebruch1951]. They are algebraic surfaces over the complex numbers. Here we consider them as smooth manifolds. The interest in them comes from Hirzebruch's result that as complex manifolds they are pairwise distinct whereas there are only two diffeomorphism types.
2 Construction and examples
Recall that if  is a complex vector bundle over
is a complex vector bundle over  , then taking the fibre-wise projective space yields the associated projective bundle:
, then taking the fibre-wise projective space yields the associated projective bundle:
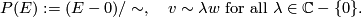
The fibres of 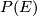 are complex projective spaces
are complex projective spaces 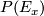 and if
and if  is a holomorphic vector bundle over a complex manifold then
is a holomorphic vector bundle over a complex manifold then 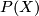 is a complex manifold. Moreover, if
is a complex manifold. Moreover, if 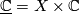 denotes the trivial complex line bundle then
denotes the trivial complex line bundle then 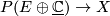 admits a canonical section
admits a canonical section
![\displaystyle s_\infty : X \to P(E \oplus \underline{\Cc}), \quad x \mapsto [x, (0, 1)]](/images/math/7/0/f/70f4e8484d37ed9f0633bf0fc95857da.png)
which takes each point of  to the ``line at infinity`` in
to the ``line at infinity`` in 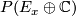 .
.
We identify 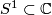 with the unit complex numbers and recall that the
with the unit complex numbers and recall that the  -sphere,
-sphere, 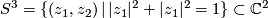 , admits the free
, admits the free  action defined by the equation:
action defined by the equation: 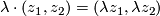 . The quotient of this action is
. The quotient of this action is 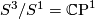 . For any integer
. For any integer 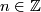 define the complex line bundle
define the complex line bundle 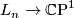 whose total space is the following quotient of
whose total space is the following quotient of 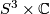
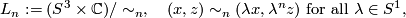
and we map 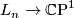 , via
, via ![[x, z] \mapsto [x] \in S^3/S^1 = \CP^1](/images/math/e/9/3/e93220407ce6d9a372690ebbab0d63f1.png) . For example,
. For example, 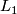 is the complex line bundle associated to the Hopf fibration and
is the complex line bundle associated to the Hopf fibration and 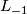 is the tautological line bundle.
is the tautological line bundle.
Definition 2.1.
For 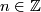 define the Hirzebruch surface
define the Hirzebruch surface 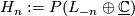 . It is a complex manifold of complex dimension
. It is a complex manifold of complex dimension  but we consider it as a smooth manifold of dimension
but we consider it as a smooth manifold of dimension  .
.
The Hirzebruch surfaces  are
are  -bundles over
-bundles over  . Hence they are closed and, by the orientation coming from the complex structure, oriented 4-dimensional manifolds.
. Hence they are closed and, by the orientation coming from the complex structure, oriented 4-dimensional manifolds.
3 Invariants
We list some invariants of the manifolds  with explanations below: let
with explanations below: let 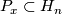 denote the fibre over
denote the fibre over 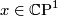 .
.
-
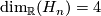 and
and 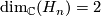 .
.
-
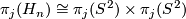 : in particular
: in particular 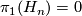 .
.
-
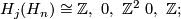 for
for 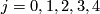 and
and 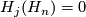 for
for 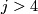 .
.
-
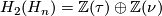 has basis with
has basis with ![\tau := [s_\infty(\Cc P^1)]](/images/math/4/d/2/4d29703ba39db73859d53c52d8820862.png) and
and ![\nu := [P_x]](/images/math/3/b/7/3b7eea132945c282c41eeebc7ddbae5a.png) .
.
- With respect to the above basis the intersection form on
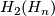 is given by the following matrix:
is given by the following matrix: 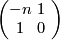 .
.
- The Euler characteristic is given by
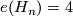 .
.
- The signature vanishes:
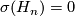 .
.
- The first Pontrjagin class of
 is zero:
is zero: 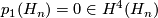 .
.
- For the complex manifold
 , the first Chern class
, the first Chern class 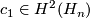 , is given by
, is given by 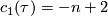 and
and 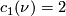 .
.
- The second Stiefel-Whitney class
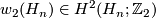 is given by
is given by 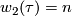 mod
mod  and
and 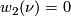 .
.
-
 is a spinable if and only if
is a spinable if and only if  is even.
is even.
3.1 Explanation
- The computation of the homotopy groups of
 follows from the homotopy sequence of a fibration and the existence of the section
follows from the homotopy sequence of a fibration and the existence of the section 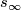 .
.
- The homology groups of
 can be computed by decomposing
can be computed by decomposing 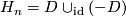 where
where 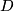 is the
is the  disc bundle associated to
disc bundle associated to 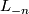 and using the Mayer-Vietoris sequence.
and using the Mayer-Vietoris sequence.
- The computation of the intersection form follows by inspecting the embedded
 -spheres which represent
-spheres which represent 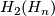 and their normal bundles: in particular we apply the fact that the self intersection number of
and their normal bundles: in particular we apply the fact that the self intersection number of 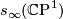 is the Euler class of
is the Euler class of 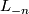 [Milnor&Stasheff1974, Problem 11-C].
[Milnor&Stasheff1974, Problem 11-C].
- The signature of
 is zero since the Hirzebruch surfaces are the boundary of the associated
is zero since the Hirzebruch surfaces are the boundary of the associated 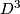 -bundle. One can also see this directly from the intersection form.
-bundle. One can also see this directly from the intersection form.
- The first Pontrjagin class vanishes as its evaluation on the fundamental class of
 is an oriented bordism invariant [Milnor&Stasheff1974, Lemma 17.3].
is an oriented bordism invariant [Milnor&Stasheff1974, Lemma 17.3].
- For the vaules of
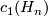 let
let  denote the complex tangent bundle of a complex manifold
denote the complex tangent bundle of a complex manifold  then
then 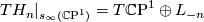 and
and 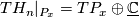 . Moreover we have
. Moreover we have 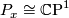 and
and ![\langle c_1(T\CP^1), [\CP^1] \rangle = 2](/images/math/0/2/0/0205d0d6e65b991d9f097ee0dfecd9cc.png) and
and ![\langle c_1(L_n), [\CP^1]\rangle = n](/images/math/b/d/0/bd08e63daf4c08c1f008f3d54187f03b.png) . Both of these equalities are justified by the fact that the first Chern class of a complex line bundle equals the Euler class of the underlying real
. Both of these equalities are justified by the fact that the first Chern class of a complex line bundle equals the Euler class of the underlying real  -plane bundle and the fact that the Euler class can be evaluated by counting the oriented intersection points of a transverse section with the zero section. For the bundle
-plane bundle and the fact that the Euler class can be evaluated by counting the oriented intersection points of a transverse section with the zero section. For the bundle 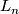 we see that there is a well-defined transverse section
we see that there is a well-defined transverse section ![[z_0, z_1] \mapsto [z_0, z_1, z_0^n - z_1^n]](/images/math/f/6/c/f6cb27684696b068924df2f4961ad099.png) with precisely
with precisely  positively oriented intersections with the zero section.
positively oriented intersections with the zero section.
- For
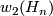 note that in general the Stiefel-Whitney classes are of a complex manifold are the mod
note that in general the Stiefel-Whitney classes are of a complex manifold are the mod  reductions of the Chern classes [Milnor&Stasheff1974, Problem 14-B].
reductions of the Chern classes [Milnor&Stasheff1974, Problem 14-B].
4 Classification
Theorem 4.1 [Hirzebruch1951].
For the smooth manifolds 
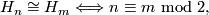
where 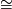 means diffeomorphic. Moreover as complex manifolds
means diffeomorphic. Moreover as complex manifolds
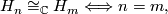
where 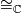 means complex diffeomorphic.
means complex diffeomorphic.
For the first statement we see that parity of the intersection form implies that if  is diffeomorphic to
is diffeomorphic to 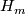 , then
, then 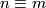 mod
mod  . On the other hand the smooth Hirzebruch surfaces are the total spaces of the 2-sphere bundle of a 3-dimensional vector bundle over
. On the other hand the smooth Hirzebruch surfaces are the total spaces of the 2-sphere bundle of a 3-dimensional vector bundle over  and these bundles are classified by
and these bundles are classified by 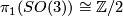 (note that
(note that  is diffeomorphic to
is diffeomorphic to 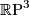 ). Thus there are precisely two diffeomorphism types of Hirzebruch surfaces. By construction
). Thus there are precisely two diffeomorphism types of Hirzebruch surfaces. By construction 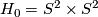 and by an easy consideration
and by an easy consideration 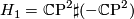 , where # is the connected sum and
, where # is the connected sum and 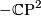 is
is 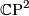 with the opposite orientation.
with the opposite orientation.
For more information on Hirzebruch surfaces, in particular why they are pairwise distinct as complex manifolds, see [Hirzebruch1951].
5 Further remarks
- The Hirzebruch surfaces show that the smooth
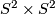 and
and 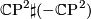 both admit infinitely many inequivalent complex structures.
both admit infinitely many inequivalent complex structures.
- The smooth manifolds
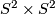 and
and 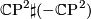 are examples of manifolds with isomorphic homotopy groups but distinct homotopy types.
are examples of manifolds with isomorphic homotopy groups but distinct homotopy types.
- The Hirzebruch surfaces are the second stage of the so called Bott towers, which are inductively constructed starting from a point as the total space of a projective bundle associated to
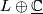 , where
, where  is a line bundle over a lower Bott tower (for more details see [Choi&Masuda&Suh2010]). The classification of the Bott towers up to homeomorphism or diffeomorphism is an interesting open problem. In particular one can ask whether the integral cohomology ring determines the homeomorphism or diffeomorphism type as it does for Hirzebruch surfaces. For 3-stage Bott towers Choi, Masuda and Suh [Choi&Masuda&Suh2010, Theorem 1.4] prove that the cohomology ring determines the diffeomorphism type.
is a line bundle over a lower Bott tower (for more details see [Choi&Masuda&Suh2010]). The classification of the Bott towers up to homeomorphism or diffeomorphism is an interesting open problem. In particular one can ask whether the integral cohomology ring determines the homeomorphism or diffeomorphism type as it does for Hirzebruch surfaces. For 3-stage Bott towers Choi, Masuda and Suh [Choi&Masuda&Suh2010, Theorem 1.4] prove that the cohomology ring determines the diffeomorphism type.
- The Hirzebruch surfaces give examples where the isotopy classes of certain diffeomorphims do not contain holomorphic maps (in this case because the diffeomorphisms do not preserve the first Chern class). For example, the connected sum of complex conjugation in both factors of
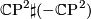 is not isotopic to a holomorphic map.
is not isotopic to a holomorphic map.
6 References
- [Choi&Masuda&Suh2010] S. Choi, D. Masuda and D. Y. Suh, Topological classification of generalized Bott towers, Trans. Amer. Math. Soc. 362 (2010), no. 2, 1097–1112. MR2551516 (2011a:57050) Zbl 1195.57060
- [Hirzebruch1951] F. Hirzebruch, Über eine Klasse von einfachzusammenhängenden komplexen Mannigfaltigkeiten, Math. Ann. 124 (1951), 77–86. MR0045384 (13,574e) Zbl 0043.30302
- [Milnor&Stasheff1974] J. W. Milnor and J. D. Stasheff, Characteristic classes, Princeton University Press, Princeton, N. J., 1974. MR0440554 (55 #13428) Zbl 1079.57504