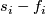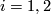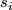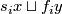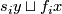Embeddings of manifolds with boundary: classification
|
The users responsible for this page are: Mikhail Fedorov, Garaev Timur. No other users may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Introduction
In this page we present results on embeddings of manifolds with non-empty boundary into Euclidean space.
In  5 we introduce an invariant of embedding of a
5 we introduce an invariant of embedding of a  -manifold in
-manifold in  -space for even
-space for even  .
In
.
In  7 which is independent from
7 which is independent from  4,
4,  5 and
5 and  6 we state generalisations of theorems from
6 we state generalisations of theorems from  2 to highly-connected manifolds.
2 to highly-connected manifolds.
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3]. In those pages mostly results for closed manifolds are stated.
3]. In those pages mostly results for closed manifolds are stated.
If the category is omitted, then we assume the smooth (DIFF) category. Denote 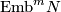 the set of all embeddings
the set of all embeddings 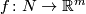 up to isotopy. We denote by
up to isotopy. We denote by 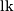 the linking coefficient [Seifert&Threlfall1980,
the linking coefficient [Seifert&Threlfall1980,  77] of two disjoint cycles.
77] of two disjoint cycles.
We state the simplest results. These results can be deduced from the Haefliger-Weber deleted product criterion [Skopenkov2006,  5], see [Haefliger1963, 6.4], [Skopenkov2002, Theorem 1.1
5], see [Haefliger1963, 6.4], [Skopenkov2002, Theorem 1.1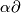 ] for the DIFF case and [Skopenkov2002, Theorem 1.3
] for the DIFF case and [Skopenkov2002, Theorem 1.3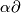 ] for the PL case. For some results we present direct proofs, which are easier than deduction from this criterion.
] for the PL case. For some results we present direct proofs, which are easier than deduction from this criterion.
We do not claim the references we give are references to original proofs.
2 Embedding and unknotting theorems
Theorem 2.1.
Assume that  is a compact connected
is a compact connected  -manifold.
-manifold.
(a) Then  embeds into
embeds into 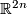 .
.
(b) If  has non-empty boundary, then
has non-empty boundary, then  embeds into
embeds into 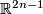 .
.
Part (a) is well-known strong Whitney embedding theorem. The first proof of (b) presented below is essentially contained in [Hirsch1961a, Theorem 4.6] for the Diff case, and in references for Theorem 7.1 below or in [Horvatic1971, Theorem 5.2] for the PL case.
Theorem 2.2.
Assume that  is a compact connected
is a compact connected  -manifold and either
-manifold and either
(a) 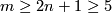 or
or
(b)  has non-empty boundary and
has non-empty boundary and 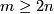 .
.
Then any two embeddings of  into
into 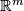 are isotopic.
are isotopic.
Part (a) is Whitney-Wu Unknotting Theorem, see [Skopenkov2016c,  2, Theorems 2.1, 2.2].
Part (b) in the case
2, Theorems 2.1, 2.2].
Part (b) in the case 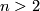 is proved in [Edwards1968,
is proved in [Edwards1968,  4, Corollary 5]. The case
4, Corollary 5]. The case  is clear. The case
is clear. The case  can be proved using the ideas presented below.
can be proved using the ideas presented below.
The inequality in part (b) is sharp by Proposition 4.1.
These basic results can be generalized to highly-connected manifolds (see  7).
In particular, both parts of Theorem 2.1 are special cases of Theorem 7.2.
7).
In particular, both parts of Theorem 2.1 are special cases of Theorem 7.2.
All theorems for manifolds with non-empty boundary stated in  2 and
2 and  7 can be proved using
7 can be proved using
- analogous results for immersions of manifolds stated in
 9, and general position ideas, see e.g. the first proof of Theorem 2.1.b in
9, and general position ideas, see e.g. the first proof of Theorem 2.1.b in  3.
3.
- handle decomposition, see e.g. the second proof of Theorem 2.1.b in
 3.
3.
Observe that the `handle decomposition' proof is essentially a `straightening' of the `immersion' proof because the required results on immersions are proved using handle decomposition.
3 Proofs of Theorem 2.1.b and Theorem 2.2.b
In this section we work only in smooth category. The first proof of Theorem 2.1.b uses immersions, while the second does not.
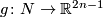 . Since
. Since  is connected and has non-empty boundary, it follows that
is connected and has non-empty boundary, it follows that  collapses to an
collapses to an  -dimensional subcomplex
-dimensional subcomplex 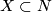 of some triangulation of
of some triangulation of  . Since
. Since 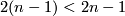 , by general position we may assume that
, by general position we may assume that 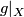 is an embedding. Since
is an embedding. Since  is an immersion, it follows that
is an immersion, it follows that  has a sufficiently small tubular neighbourhood
has a sufficiently small tubular neighbourhood 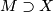 such that
such that 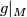 is embedding. Since tubular neighbourhood is unique up to homeomorphism, there exists a homeomorphism
is embedding. Since tubular neighbourhood is unique up to homeomorphism, there exists a homeomorphism 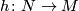 . The composition
. The composition 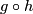 is an embedding of
is an embedding of  .
.
For the second proof we need some lemmas.
Lemma 3.1. [Wall1966]
Assume that  is a closed connected
is a closed connected  -manifold. Then
-manifold. Then  have handle decomposition with indices of attaching maps at most
have handle decomposition with indices of attaching maps at most 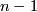 .
.
Lemma 3.2.
Assume that  is a compact
is a compact  -manifold,
-manifold, 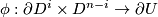 is an embedding with
is an embedding with 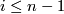 , and
, and 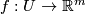 is an embedding.
is an embedding.
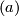 If
If 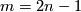 , then there is an extension of
, then there is an extension of  to an embedding of
to an embedding of 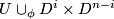 .
.
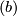 Assume also that there is an embedding
Assume also that there is an embedding 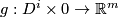 such that
such that 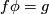 on
on 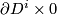 . Suppose that on
. Suppose that on 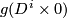 there is a field of
there is a field of 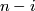 linear independed normal vectors whose restriction to
linear independed normal vectors whose restriction to 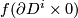 is tangent to
is tangent to 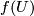 . Then
. Then 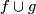 extends to a embedding
extends to a embedding 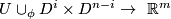 .
.
 with attaching maps
with attaching maps 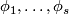 of indices at most
of indices at most  . Denote by
. Denote by 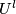 the manifold obtained from
the manifold obtained from  by the attaching first
by the attaching first 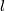 handles. Take any embedding
handles. Take any embedding 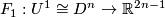 . Let us define an embedding
. Let us define an embedding 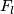 of
of 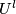 using an embedding
using an embedding 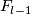 of
of 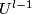 . Since the index
. Since the index  of
of 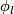 is smaller than
is smaller than  , by Lemma 3.2 there is extension of
, by Lemma 3.2 there is extension of 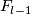 to an embedding
to an embedding 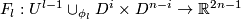 , where
, where 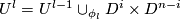 .
.

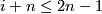 and
and 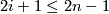 , by general position there is an embedding
, by general position there is an embedding 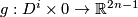 such that
such that 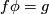 on
on 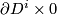 and
and 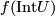 has a finite number of intersections points with
has a finite number of intersections points with 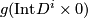 . Then by an isotopy
. Then by an isotopy 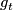 , where
, where 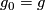 , fixed on
, fixed on 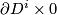 we can "push out" the self-intersection points toward
we can "push out" the self-intersection points toward 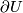 so that
so that 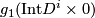 does not intersect
does not intersect 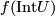 . Then
. Then 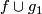 is an embedding.
is an embedding.
Denote by  the
the 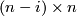 matrix whose rightmost
matrix whose rightmost 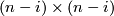 block is the identity matrix, and whose other elements are zeros. Denote by
block is the identity matrix, and whose other elements are zeros. Denote by  the field of
the field of 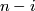 normal vectors on
normal vectors on 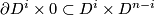 such that the
such that the  -th vector has coordinates equal to the
-th vector has coordinates equal to the  -th row in
-th row in  . Then the vector field
. Then the vector field 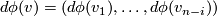 is tangent to
is tangent to 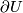 . For
. For 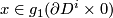 denote by
denote by 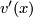 the projection of
the projection of 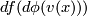 to the intersection of normal space to
to the intersection of normal space to 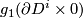 at
at  , and tangent space to
, and tangent space to 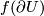 at
at  . Since
. Since 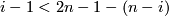 , it follows that
, it follows that 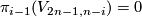 . Hence there is an extension of
. Hence there is an extension of  to an linearly independent field of vectors normal to
to an linearly independent field of vectors normal to 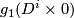 . Then by Lemma 3.2.(b) there is an extension of
. Then by Lemma 3.2.(b) there is an extension of 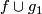 to an embedding of
to an embedding of 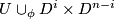 .
.

In the proof of Theorem 2.2 we will use Lemma 3.1 and Lemma 3.3.(a).
Lemma 3.3.
Assume that  is a compact
is a compact  -manifold,
-manifold, 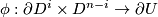 is an embedding with
is an embedding with 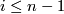 ,
, 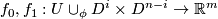 are embeddings and
are embeddings and ![F:U\times [0, 1]\to \mathbb{R}^m\times [0, 1]](/images/math/0/a/5/0a5afa6109b3c76ed5b39705fbe747a6.png) is a concordance between
is a concordance between 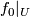 and
and 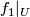 .
.
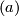 If
If 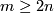 , then there is an extension of
, then there is an extension of  to a concordance between
to a concordance between  and
and  .
.
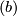 Assume also that there is a concordance
Assume also that there is a concordance ![G:D^i\times 0\times [0, 1]:\mathbb{R}^m\times [0, 1]](/images/math/7/6/7/7673e4c9b3f109db6df179275aa770ea.png) between
between  and
and 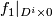 , and on
, and on ![G(D^i\times 0\times [0, 1])](/images/math/f/c/a/fca2beb45e712aea38b8468ffe73aa06.png) there is a field of
there is a field of 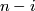 linear independent normal vectors whose restrictions to
linear independent normal vectors whose restrictions to ![G(\partial D^i\times 0\times [0, 1])](/images/math/9/c/c/9cc2f3be82a33e109eee7e7e9cabc33e.png) , to
, to 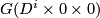 , and to
, and to 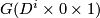 are tangent to
are tangent to ![\displaystyle F(U\times [0, 1])\quad\text{to}\quad f_0(D^i\times D^{n-i})\times 0,\quad\text{and to}\quad f_1(D^i\times D^{n-i})\times 1,](/images/math/f/f/d/ffd7ad38f5cca1a0734fe05216e65aac.png)
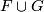 extends to a concordance between
extends to a concordance between  and
and  .
.
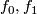 any two embeddings of
any two embeddings of  into
into 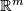 .
By the Concordance Implies Isotopy Theorem it suffices to prove that there is a concordance between
.
By the Concordance Implies Isotopy Theorem it suffices to prove that there is a concordance between  and
and  . In order to prove that observe that by Lemma 3.1 there is a handle decomposition of
. In order to prove that observe that by Lemma 3.1 there is a handle decomposition of  with attaching maps of indices at most
with attaching maps of indices at most 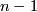 . Denote by
. Denote by 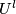 the manifold obtained from
the manifold obtained from 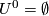 by the attaching the first
by the attaching the first 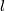 handles, starting with?
handles, starting with? 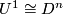 . Define a concordance
. Define a concordance ![F_l:U^l\times [0, 1] \to \mathbb R^m \times [0, 1]](/images/math/c/8/f/c8fc688383c938817e2af703f09348bd.png) recursively. Take any concordance
recursively. Take any concordance ![F_1:U^1\times [0, 1] \to \mathbb R^m \times [0, 1]](/images/math/5/d/a/5da41d0f9627f07b25eed4568694be9f.png) between
between 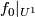 and
and 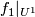 . Let us define a concordance
. Let us define a concordance 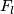 between
between 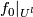 and
and 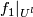 using a concordance
using a concordance 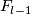 of
of 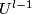 between
between 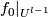 and
and 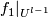 . For this denote by
. For this denote by 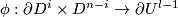 the
the 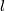 -th attaching map. Since
-th attaching map. Since 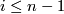 , by Lemma 3.3.(a) there is an extension of
, by Lemma 3.3.(a) there is an extension of 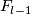 to a concordance
to a concordance ![\displaystyle F_{l}:U^{l}\times [0, 1]\to\mathbb{R}^m\times [0, 1]](/images/math/9/2/d/92d569ae37a3f5056e69ae40f1793978.png)
 and
and  to
to 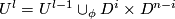 .
.

![D^i\times D^{n-i}\times [0, 1]](/images/math/8/8/c/88cd3df672a5115775ffedfb544d5bb9.png) and
and ![D^i\times [0, 1]\times D^{n-i}](/images/math/e/c/c/ecc8260a7d0e17d2ea80f735dd1f84b9.png) . Define map
. Define map ![\displaystyle \bar{\phi}:\partial (D^i\times [0, 1])\times D^{n-i}\to \partial U\times[0, 1]\cup_{\phi\times 0} D^i\times D^{n-i}\times 0 \cup_{\phi\times 1} D^i\times D^{n-i}\times 1](/images/math/0/7/2/072e9c7b08fb27a39c991a4f39e66c90.png)
Tex syntax error
![\displaystyle \dim(D^i\times 0\times [0, 1]) + \dim (U\times [0, 1])\leq (i+1)+(n+1)\quad\text{and}\quad 2\dim(D^i\times 0\times [0, 1])+1\leq 2n+1\leq m+1,](/images/math/e/2/f/e2f26595053cad0cb5f36bee49feae8f.png)
![\displaystyle G: D^i\times 0\times [0, 1]\to \mathbb R^m\times [0, 1]](/images/math/c/9/d/c9d97bc144c9fb07e80ab6036a323230.png)
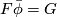 on
on ![\partial (D^i \times 0\times [0, 1])](/images/math/4/7/5/47580101248722766a17873fe2537b54.png) and
and ![F(\mbox{Int} (U\times [0, 1]))](/images/math/4/1/0/4107ba155251147427656118445b1e23.png) has a finite number of intersection points with
has a finite number of intersection points with ![G(\mbox{Int}( D^i\times 0\times [0, 1]))](/images/math/f/a/a/faab5cd0d220270034ac52657c616897.png) . Then by an isotopy
. Then by an isotopy 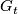 , where
, where 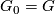 , fixed on
, fixed on ![\partial (D^i\times 0\times [0, 1])](/images/math/f/e/2/fe2c72ed3c40eb59b3c08c33b008f134.png) we can "push out" the self-intersection points toward
we can "push out" the self-intersection points toward ![F(\partial (U\times [0, 1]))](/images/math/2/b/2/2b2fc6ab2e202f22d54317673c6d2997.png) so that
so that ![G_1(D^i\times 0\times [0, 1])](/images/math/8/9/a/89aa9e32478b85ce4b2076ccb36ec156.png) does not intersect
does not intersect ![G(U\times [0, 1])](/images/math/8/8/e/88e8188653e195ec591958c50130d42b.png) . Then
. Then 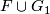 is an concordance between the restrictions of
is an concordance between the restrictions of  and
and  on
on 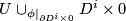 .
.
Denote by  the
the 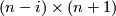 matrix whose rightmost
matrix whose rightmost 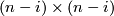 submatrix is the identity matrix, and whose other elements are zeroes. Denote by
submatrix is the identity matrix, and whose other elements are zeroes. Denote by  the field of
the field of 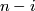 normal vectors on
normal vectors on ![\partial (D^i\times 0\times [0, 1])\subset D^i\times D^{n-i}\times [0, 1]](/images/math/b/7/8/b789d65c23e15ba8503d24c2880d1f69.png) whose
whose  -th vector has coordinates equal to the
-th vector has coordinates equal to the  -th row in
-th row in  . Then
. Then 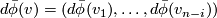 is the vector field tangent to
is the vector field tangent to ![\bar{\phi}(\partial (D^i\times [0, 1])\times D^{n-i})](/images/math/f/1/d/f1d95768a571ec71c70e51167a9e17ce.png) . For
. For ![x\in G_1(\partial (D^i\times 0\times [0, 1])](/images/math/b/c/2/bc29f11b3848c0b13c8b914de3d929fc.png) denote by
denote by 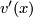 the projection of
the projection of 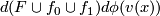 to the intersection of normal space to
to the intersection of normal space to ![G_1(D^i\times 0\times [0, 1])](/images/math/8/9/a/89aa9e32478b85ce4b2076ccb36ec156.png) at
at  , and tangent space to
, and tangent space to ![F(\partial(U\times [0, 1]))](/images/math/f/1/0/f103f0347304bdd515fa0451a0c7a739.png) at
at  . Since
. Since 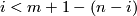 , it follows that
, it follows that 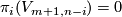 . Hence there is an extension of
. Hence there is an extension of 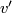 to a linear independent field of vectors normal to
to a linear independent field of vectors normal to ![G_1(D^i\times 0\times [0, 1])](/images/math/8/9/a/89aa9e32478b85ce4b2076ccb36ec156.png) . Then by Lemma 3.3.(b) there is an extension of
. Then by Lemma 3.3.(b) there is an extension of 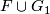 to a concordance
to a concordance ![(U \cup_{\phi} D^i\times D^{n-i})\times [0, 1]](/images/math/f/3/2/f3230ae3f2e8fb41d889a25d4f8fa113.png) .
.

4 Example of non-isotopic embeddings
The following example is folklore.
Example 4.1.
Let ![N=S^k\times [0, 1]](/images/math/2/6/6/266b1d722e6d382c691b340077590a2a.png) be the cylinder over
be the cylinder over 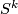 .
.
(a) Then there exist non-isotopic embeddings of  into
into 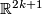 .
.
(b) Then for each 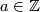 there exist an embedding
there exist an embedding 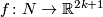 such that
such that 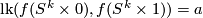 .
.
(c) Then 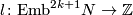 defined by the formula
defined by the formula ![l([f]) = \mathrm{lk}(f(S^k\times 0), f(S^k\times 1))](/images/math/3/1/2/3125945705a217c79f1231d2fab4cfad.png) is well-defined and is a bijection for
is well-defined and is a bijection for 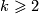 .
.
Proof.
Proof of part (b). Informally speaking by twisting a ribbon one can obtain arbitrary value of linking coefficient. Let 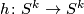 be a map of degree
be a map of degree  . (To prove part (a) it is sufficient to take as
. (To prove part (a) it is sufficient to take as  the identity map of
the identity map of 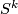 as a map of degree one and the constant map as a map of degree zero.)
Define
as a map of degree one and the constant map as a map of degree zero.)
Define ![g\colon S^k\times [0, 1] \to D^{k+1}\times S^k](/images/math/e/a/5/ea567696294b1eace2e85ead0c479d90.png) by the formula
by the formula 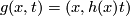 .
.
Let 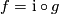 , where
, where 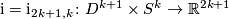 is the standard embedding.Thus
is the standard embedding.Thus 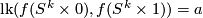 .
.
Proof of part (c). Clearly 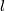 is well-defined. By (b)
is well-defined. By (b) 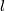 is surjective. Now take any two embeddings
is surjective. Now take any two embeddings 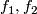 such that
such that ![l([f_1]) = l([f_2])](/images/math/c/5/3/c5301a619ec25514327c3ce383e5828f.png) . Each embedding of a cylinder gives an embedding of a sphere with a normal field. Moreover, isotopic embeddings of cylinders gives isotopic embeddings of spheres with normal fields.
. Each embedding of a cylinder gives an embedding of a sphere with a normal field. Moreover, isotopic embeddings of cylinders gives isotopic embeddings of spheres with normal fields.
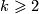 Unknotting Spheres Theorem implies that there exists an isotopy of
Unknotting Spheres Theorem implies that there exists an isotopy of 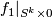 and
and 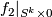 . Thus we can assume
. Thus we can assume 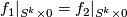 . Since
. Since ![l([f_1]) = l([f_2])](/images/math/c/5/3/c5301a619ec25514327c3ce383e5828f.png) it follows that normal fields on
it follows that normal fields on 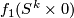 and
and 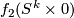 are homotopic in class of normal fields. This implies
are homotopic in class of normal fields. This implies  and
and 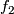 are isotopic.
are isotopic. 
Denote 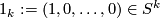 .
.
Example 4.2.
Let 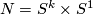 . Assume
. Assume 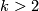 . Then there exists a bijection
. Then there exists a bijection 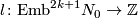 defined by the formula
defined by the formula ![l([f])=\mathrm{lk}(S^k\times1_1, S^k\times-1_1)](/images/math/8/7/9/879022d79ae68bb4c52d65ea476828cc.png) .
.
The surjectivity of 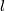 is given analogously to Proposition 4.1(b).
The injectivity of
is given analogously to Proposition 4.1(b).
The injectivity of 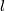 follows from forgetful bijection
follows from forgetful bijection ![\mathrm{Emb}^{2k+1}N_0\to\mathrm{Emb}^{2k+1}S_k\times[0,1]](/images/math/6/7/9/67921ffee219afa01db832382b35c7d3.png) between embeddings of
between embeddings of  and a cylinder.
and a cylinder.
This example shows that Theorem 7.4 fails for 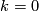 .
.
Example 4.3.
Let 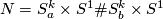 be the connected sum of two tori. Then there exists a surjection
be the connected sum of two tori. Then there exists a surjection 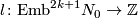 defined by the formula
defined by the formula ![l([f])=\mathrm{lk}(f(S^k_a\times1_1), f(S^k_b\times1_1))](/images/math/a/9/6/a9636bff34a3119f824c57f0633bbf73.png) .
.
To prove the surjectivity of 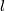 it is sufficient to take linked
it is sufficient to take linked  -spheres in
-spheres in 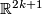 and consider an embedded boundary connected sum of ribbons containing these two spheres.
and consider an embedded boundary connected sum of ribbons containing these two spheres.
Example 4.4.
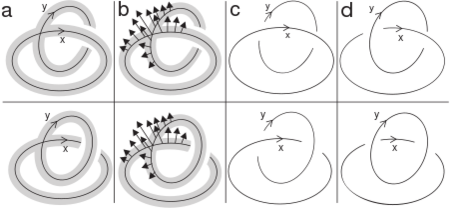
(a) Let  be the punctured 2-torus containing the meridian
be the punctured 2-torus containing the meridian  and the parallel
and the parallel  of the torus. For each embedding
of the torus. For each embedding 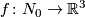 denote by
denote by  the normal field of
the normal field of  -length vectors to
-length vectors to 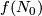 defined by orientation on
defined by orientation on  (see figure (b)). Then there exists a surjection
(see figure (b)). Then there exists a surjection 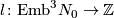 defined by the formula
defined by the formula ![l([f])=\mathrm{lk}(f(x), s(y))](/images/math/b/e/b/beb8b4bbd1013fc224dda3c91b24841e.png) .
.
(b) Let 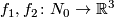 be two embeddings shown on figure (a).
Figure (c) shows that
be two embeddings shown on figure (a).
Figure (c) shows that 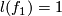 and
and 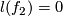 which proves the intuitive fact that
which proves the intuitive fact that  and
and 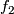 are not isotopic.
(Notice that the restrictions of
are not isotopic.
(Notice that the restrictions of  and
and 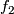 on
on 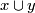 are isotopic!)
If we use the opposite normal vector field
are isotopic!)
If we use the opposite normal vector field 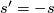 , the values of
, the values of 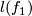 and
and 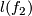 will change but will still be different (see figure (d)).
will change but will still be different (see figure (d)).
5 Seifert linking form
For a simpler invariant see [Skopenkov2022] and references therein.
In this section assume that
-
 is any closed orientable connected
is any closed orientable connected  -manifold,
-manifold,
-
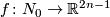 is any embedding,
is any embedding,
- if the (co)homology coefficients are omitted, then they are
 ,
,
-
 is even and
is even and 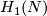 is torsion free (these two assumptions are not required in Lemma \ref{lmm::saeki}).
is torsion free (these two assumptions are not required in Lemma \ref{lmm::saeki}).
By  we denote the closure of the complement in
we denote the closure of the complement in  to an closed
to an closed  -ball. Thus
-ball. Thus 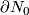 is the
is the  -sphere.
-sphere.
Lemma 5.1. There exists a nowhere vanishing normal vector field to 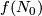 .
.
This is essentially a folklore result, see an unpublished update of [Tonkonog2010] and [Fedorov2021, Lemma 5.1], cf. [Saeki1999, Lemma 4.1].
Denote by  two disjoint
two disjoint  -cycles in
-cycles in  with integer coefficients. Denote
with integer coefficients. Denote
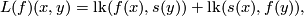
where  is a nowhere vanishing normal field to
is a nowhere vanishing normal field to 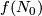 and
and 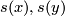 are the results of the shift of
are the results of the shift of 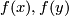 by
by  .
.
Lemma 5.2 ( is well-defined).
The integer
is well-defined).
The integer 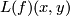 :
:
- is well-defined, i.e., does not change when
 is replaced by
is replaced by 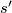 ,
,
- does not change when
 or
or  are changed to homologous cycles and,
are changed to homologous cycles and,
- does not change when
 is changed to an isotopic embedding.
is changed to an isotopic embedding.
The first bullet was stated and proved in unpublished update of [Tonkonog2010] and in [Fedorov2021, Lemma 5.3], other two bullets are simple.
Lemma 5.2 implies that 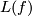 generates a bilinear form
generates a bilinear form
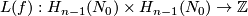
denoted by the same letter and called Seifert linking form.
Denote by 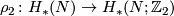 the reduction modulo
the reduction modulo  . Define the dual to Stiefel-Whitney class
. Define the dual to Stiefel-Whitney class 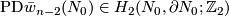 to be the class of the cycle on which two general position normal fields to
to be the class of the cycle on which two general position normal fields to 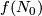 are linearly dependent.
are linearly dependent.
Lemma 5.3.
For every 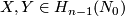 the following equality holds:
the following equality holds:
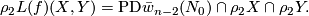
This Lemma was stated in a unpublished update of [Tonkonog2010]; a proof is presented in [Fedorov2021, Lemma 6.1] using the idea from that update. See also an analogous lemma for closed manifolds in [Crowley&Skopenkov2016, Lemma 2.2].
6 Classification theorems
Here we state classification results that are neither unknotting nor embeddability theorems for manifolds with boundary.
Let  be a closed orientable connected
be a closed orientable connected  -manifold.
By
-manifold.
By  we denote the complement in
we denote the complement in  to an open
to an open  -ball. Thus
-ball. Thus 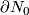 is the
is the  -sphere.
For a free Abelian group
-sphere.
For a free Abelian group  , let
, let 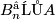 be the group of bilinear forms
be the group of bilinear forms 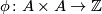 such that
such that 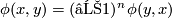 and
and 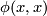 is even for each
is even for each  (the second condition automatically holds for n odd).
(the second condition automatically holds for n odd).
Definition 6.1.
For each even  define an invariant
define an invariant 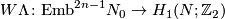 . For each embedding
. For each embedding 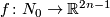 construct any PL embedding
construct any PL embedding 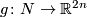 by adding a cone over
by adding a cone over 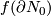 . Now let
. Now let ![W\Lambda([f]) = W(g)](/images/math/4/f/1/4f112155386838fd013fd36dafab2f2b.png) , where
, where  is Whitney invariant, [Skopenkov2016e,
is Whitney invariant, [Skopenkov2016e,  5].
5].
Lemma 6.2.
The invariant 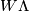 is well-defined for
is well-defined for 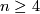 .
.
Proof.
Note that Unknotting Spheres Theorem implies that 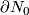 unknots in
unknots in 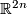 . Thus
. Thus 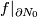 can be extended to embedding of an
can be extended to embedding of an  -ball
-ball  into
into 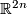 . Unknotting Spheres Theorem implies that
. Unknotting Spheres Theorem implies that  -sphere unknots in
-sphere unknots in 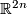 . Thus all extensions of
. Thus all extensions of  are isotopic in PL category.
Note also that if
are isotopic in PL category.
Note also that if  and
and  are isotopic then their extensions are isotopic as well.
And Whitney invariant
are isotopic then their extensions are isotopic as well.
And Whitney invariant  is invariant for PL embeddings.
is invariant for PL embeddings.

Definition 6.3 of 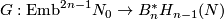 if
if  is even and
is even and 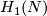 is torsion-free.
Take a collection
is torsion-free.
Take a collection
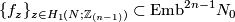 such that
such that
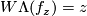 .
For each
.
For each  such that
such that 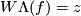 define
define
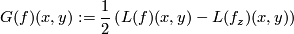
where
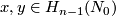 .
.
Note also that  depends on choice of collection
depends on choice of collection 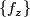 . The following Theorems hold for any choice of
. The following Theorems hold for any choice of 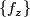 .
.
Theorem 6.4.
Let  be a closed connected orientable
be a closed connected orientable
 -manifold with
-manifold with 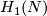 torsion-free,
torsion-free, 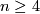 ,
,  even.
The map
even.
The map
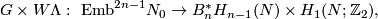
is one-to-one.
Lemma 6.5.
For each even 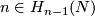 and each
and each  the following equality holds:
the following equality holds: 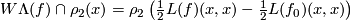 .
.
An equivalemt statement of Theorem 6.4:
Theorem 6.6.
Let  be a closed connected orientable
be a closed connected orientable  -manifold with
-manifold with 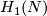 torsion-free,
torsion-free, 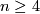 ,
,  even. Then
even. Then
(a) The map 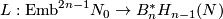 is an injection.
is an injection.
(b) The image of  consists of all symmetric bilinear forms
consists of all symmetric bilinear forms 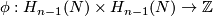 such that
such that 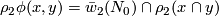 . Here
. Here 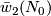 is the normal Stiefel-Whitney class.
is the normal Stiefel-Whitney class.
This is the main Theorem of [Tonkonog2010]
7 A generalization to highly-connected manifolds
For simplicity in this paragraph we consider only punctured manifolds, see  8 for a generalization.
8 for a generalization.
Denote by  a closed
a closed  -manifold. By
-manifold. By  denote the complement in
denote the complement in  to an open
to an open  -ball. Thus
-ball. Thus 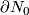 is the
is the  -sphere.
-sphere.
Theorem 7.1.
Assume that  is a closed
is a closed  -connected
-connected  -manifold.
-manifold.
(a) If 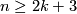 , then
, then  embeds into
embeds into 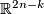 .
.
(b) If 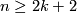 and
and 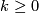 , then
, then  embeds into
embeds into 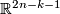 .
.
Part (a) is proved in [Haefliger1961, Existence Theorem (a)] for the Diff case and in [Penrose&Whitehead&Zeeman1961, Theorem 1.1], [Irwin1965, Corollary 1.3] for PL case.
Part (b) is proved in [Hirsch1961a, Corollary 4.2] for the Diff case and in [Penrose&Whitehead&Zeeman1961, Theorem 1.2] for the PL case.
Theorem 7.2.
Assume that  is a closed
is a closed  -connected
-connected  -manifold.
-manifold.
(a) If 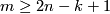 and
and 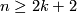 , then any two embeddings of
, then any two embeddings of  into
into 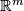 are isotopic.
are isotopic.
(b) If 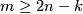 and
and 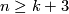 and
and 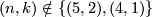 then any two embeddings of
then any two embeddings of  into
into 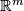 are isotopic.
are isotopic.
Part (a) is Theorem 2.4 of the survey [Skopenkov2016c,  2], and is proved in [Zeeman1963, Corollary 2 of Theorem 24 in Chapter 8] and [Haefliger1961, Existence Theorem (b) in p. 47].
2], and is proved in [Zeeman1963, Corollary 2 of Theorem 24 in Chapter 8] and [Haefliger1961, Existence Theorem (b) in p. 47].
Part (b) is proved in [Hudson1969, Theorem 10.3] for the PL case, using concordance implies isotopy theorem.
For 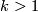 part (b) is a corollary of Theorem 7.4 below. For
part (b) is a corollary of Theorem 7.4 below. For 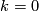 part (b) coincides with Theorem 2.2b.
part (b) coincides with Theorem 2.2b.
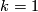 . By Theorem 9.6 below every two immersions of
. By Theorem 9.6 below every two immersions of  into
into 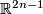 are regulary homotopic. Hence for every two embeddings
are regulary homotopic. Hence for every two embeddings 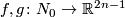 there exist an immersion
there exist an immersion ![F\colon N_0\times[0,1]\to\mathbb R^{2n-1}\times[0,1]](/images/math/7/9/6/7963693062b9ca3ce3d3f649be11320a.png) such that
such that 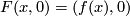 and
and 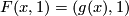 for each
for each 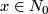 . It follows from Theorem 8.3 that
. It follows from Theorem 8.3 that  collapses to an
collapses to an  -dimensional subcomplex
-dimensional subcomplex 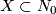 of some triangulation of
of some triangulation of  . By general position we may assume that
. By general position we may assume that ![F|_{X\times[0,1]}](/images/math/8/c/5/8c58be4ffc545b6549527ed446a6de3a.png) is an embedding, because
is an embedding, because 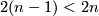 . Since
. Since  is an immersion, it follows that
is an immersion, it follows that  has a sufficiently small regular neighbourhood
has a sufficiently small regular neighbourhood 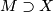 such that
such that ![F|_{M\times[0,1]}](/images/math/2/b/a/2ba2ff85f9227591c2967fbb841c3b37.png) is an embedding. Since regular neighbourhood is unique up to homeomorphism, there exists a homeomorphism
is an embedding. Since regular neighbourhood is unique up to homeomorphism, there exists a homeomorphism 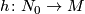 . It is clear that
. It is clear that  is isotopic to
is isotopic to  and
and  is isotopic to
is isotopic to 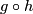 . Thus, the restriction
. Thus, the restriction ![F|_{M\times[0,1]}](/images/math/2/b/a/2ba2ff85f9227591c2967fbb841c3b37.png) is a concordance of
is a concordance of  and
and 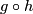 . By concordance implies isotopy Theorem
. By concordance implies isotopy Theorem  and
and  are isotopic.
are isotopic.
Conjecture 7.3.
Assume that  is a closed
is a closed  -connected
-connected  -manifold. Then any two embeddings of
-manifold. Then any two embeddings of  in
in 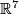 are isotopic.
are isotopic.
We may hope to get around the restrictions of Theorem 8.3 using the deleted product criterion.
Theorem 7.4.
Assume  is a closed
is a closed  -connected
-connected  -manifold. Then for each
-manifold. Then for each 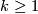 there exists a bijection
there exists a bijection
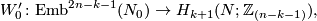
where 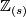 denote
denote  for
for  even and
even and 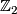 for
for  odd.
odd.
For definition of 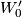 and the proof of the latter Theorem see [Skopenkov2010, Lemma 2.2(
and the proof of the latter Theorem see [Skopenkov2010, Lemma 2.2(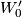 )]. The latter theorem was essentially proven in [Vrabec1989, Theorem 2.1].
Latter Theorem is essentially known result. Compare to the Theorem 6.6, which describes
)]. The latter theorem was essentially proven in [Vrabec1989, Theorem 2.1].
Latter Theorem is essentially known result. Compare to the Theorem 6.6, which describes 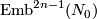 and differs from the general case.
and differs from the general case.
8 Comments on non-spherical boundary
Theorem 8.1.
Assume that  is a compact
is a compact  -connected
-connected  -manifold,
-manifold, 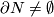 ,
, 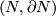 is
is  -connected and
-connected and 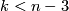 .
Then
.
Then  embeds into
embeds into 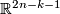 .
.
This is [Wall1965, Theorem on p.567].
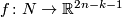 . Since
. Since  is
is  -connected it follows from Theorem 8.3 that
-connected it follows from Theorem 8.3 that  collapses to an
collapses to an 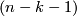 -dimensional subcomplex
-dimensional subcomplex 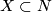 of some triangulation of
of some triangulation of  . By general position we may assume that
. By general position we may assume that 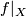 is an embedding, because
is an embedding, because 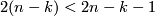 . Since
. Since  is an immersion, it follows that
is an immersion, it follows that  has a sufficiently small regular neighbourhood
has a sufficiently small regular neighbourhood 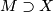 such that
such that 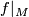 is an embedding. Since regular neighbourhood is unique up to homeomorphism, there exists a homeomorphism
is an embedding. Since regular neighbourhood is unique up to homeomorphism, there exists a homeomorphism 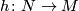 . It is clear that
. It is clear that  is an embedding.
is an embedding.
Theorem 8.2.
Assume that  is a
is a  -manifold. If
-manifold. If  has
has 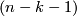 -dimensional spine,
-dimensional spine, 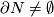 ,
, 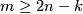 , then any two embeddings of
, then any two embeddings of  into
into 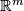 are isotopic.
are isotopic.
Proof is similar to the proof of theorem 7.2.
For a compact connected  -manifold with boundary, the property of having an
-manifold with boundary, the property of having an 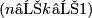 -dimensional spine is close to
-dimensional spine is close to  -connectedness. Indeed, the following theorem holds.
-connectedness. Indeed, the following theorem holds.
Theorem 8.3.
Every compact connected  -manifold
-manifold  with boundary for which
with boundary for which 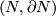 is
is  -connected,
-connected, 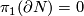 ,
,
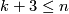 and
and 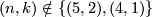 , has an
, has an 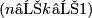 -dimensional spine.
-dimensional spine.
For this result see [Wall1964a, Theorem 5.5] and [Horvatic1969, Lemma 5.1 and Remark 5.2]. See also valuable remarks in [Levine&Lidman2018] and [Skopenkov2019].
9 Comments on immersions
Theorem 9.1.[Smale-Hirsch; [Hirsch1959] and [Haefliger&Poenaru1964]]
The space of immersions of a manifold in  is homotopy equivalent to the space of linear monomorphisms from
is homotopy equivalent to the space of linear monomorphisms from  to
to  .
.
Theorem 9.2.[[Hirsch1959, Theorem 6.4]]
If  is immersible in
is immersible in 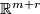 with a normal
with a normal  -field, then
-field, then  is immersible in
is immersible in  .
.
Theorem 9.3.
Every  -manifold
-manifold  with non-empty boundary is immersible in
with non-empty boundary is immersible in 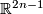 .
.
Theorem 9.4.[Whitney; [Hirsch1961a, Theorem 6.6]]
Every  -manifold
-manifold  is immersible in
is immersible in 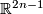 .
.
Denote by 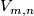 is Stiefel manifold of
is Stiefel manifold of  -frames in
-frames in  .
.
Theorem 9.5.
Suppose  is a
is a  -manifold with non-empty boudary,
-manifold with non-empty boudary, 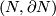 is
is  -connected. Then
-connected. Then  is immersible in
is immersible in  for each
for each 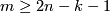 .
.
Proof.
It suffices to show that exists an immersion of  in
in 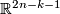 .
It suffices to show that exists a linear monomorphism from
.
It suffices to show that exists a linear monomorphism from  to
to 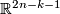 .
Let us construct such a linear monomorphism by skeleta of
.
Let us construct such a linear monomorphism by skeleta of  .
It is clear that a linear monomorphism exists on
.
It is clear that a linear monomorphism exists on  -skeleton of
-skeleton of  .
.
The obstruction to extend the linear monomorphism from 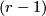 -skeleton to
-skeleton to  -skeleton lies in
-skeleton lies in 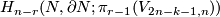 .
.
For 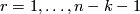 we know
we know 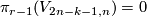 .
For
.
For 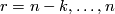 we have
we have 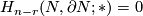 since
since 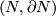 is
is  -connected and has non-empty boundary.
-connected and has non-empty boundary.
Thus the obstruction is always zero and such linear monomorphism exists.

Theorem 9.6.
Suppose  is a connected
is a connected  -manifold with non-empty boudary,
-manifold with non-empty boudary, 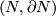 is
is  -connected and
-connected and 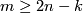 . Then every two immersions of
. Then every two immersions of  in
in  are regulary homotopic.
are regulary homotopic.
Proof.
It suffies to show that exists homomotphism of any two linear monomorphisms from  to
to 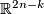 . Lets cunstruct such homotopy on each
. Lets cunstruct such homotopy on each  -skeleton of
-skeleton of  . It is clear that homotopy exists on
. It is clear that homotopy exists on  -skeleton of
-skeleton of  .
.
The obstruction to extend the homotopy from 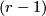 -skeleton to
-skeleton to  -skeleton lies in
-skeleton lies in 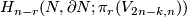 .
.
For 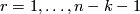 we know
we know 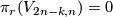 .
For
.
For 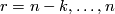 we have
we have 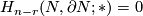 since
since 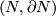 is
is  -connected and
-connected and  has non-empty boundary.
has non-empty boundary.
Thus the obstruction is always zero and such homotopy of linear monomorphisms exists.

10 References
- [Crowley&Skopenkov2016] D. Crowley and A. Skopenkov, Embeddings of non-simply-connected 4-manifolds in 7-space, I. Classification modulo knots, Moscow Math. J., 21 (2021), 43--98. arXiv:1611.04738.
- [Edwards1968] Edwards, C. H. Unknotting polyhedral homology manifolds, Michigan Math. J. 15 (1968), 81-95. MR226629 Zbl 0167.52001
- [Fedorov2021] M. Fedorov, A description of values of Seifert form for punctured n-manifolds in (2n-1)-space. Available at the arXiv:2107.02541.
- [Haefliger&Poenaru1964] Template:Haefliger&Poenaru1964
- [Haefliger1961] A. Haefliger, Plongements différentiables de variétés dans variétés., Comment. Math. Helv.36 (1961), 47-82. MR0145538 (26 #3069) Zbl 0102.38603
- [Haefliger1963] A. Haefliger, Plongements différentiables dans le domain stable., Comment. Math. Helv.37 (1963), 155-176.
- [Hirsch1959] M. W. Hirsch, Immersions of manifolds, Trans. Amer. Math. Soc. 93 (1959), 242–276. MR0119214 (22 #9980) Zbl 0118.18603
- [Hirsch1961a] M. W. Hirsch, On Imbedding Differentiable Manifolds in Euclidean Space, Annals of Mathematics, Second Series, 73(3) (1961), 566–571.
- [Horvatic1969] Template:Horvatic1969
- [Horvatic1971] K. Horvatic, On embedding polyhedra and manifolds, Trans. Am. Math. Soc. 157 (1971), 417-436.
- [Hudson1969] J. F. P. Hudson, Piecewise linear topology, W. A. Benjamin, Inc., New York-Amsterdam, 1969. MR0248844 (40 #2094) Zbl 0189.54507
- [Irwin1965] M. Irwin, Embeddings of polyhedral manifolds, Ann. of Math. (2) 82 (1965) 1–14. MR0182978 (32 #460) Zbl 0132.20003
- [Levine&Lidman2018] Template:Levine&Lidman2018
- [Penrose&Whitehead&Zeeman1961] R. Penrose, J. Whitehead and E. Zeeman, Imbedding of manifolds in Euclidean space., Ann. of Math. 73 (1961) 613–623. MR0124909 (23 #A2218) Zbl 0113.38101
- [Saeki1999] O. Saeki, On punctured 3-manifolds in 5-sphere, Hiroshima Math. J. 29 (1999) 255--272, MR1704247 (2000h:57045)
- [Seifert&Threlfall1980] Seifert, Herbert; Threlfall, William (1980), Goldman, Michael A.; Birman, Joan S. (eds.), Seifert and Threlfall: a textbook of topology, Pure and Applied Mathematics, 89, London: Academic Press Inc. [Harcourt Brace Jovanovich Publishers], ISBN 978-0-12-634850-7 MR0575168
- [Skopenkov2002] A. Skopenkov, On the Haefliger-Hirsch-Wu invariants for embeddings and immersions., Comment. Math. Helv. 77 (2002), no.1, 78-124. MRMR1898394 (2003c:57023) Zbl 1012.57035
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2010] A. Skopenkov, Embeddings of k-connected n-manifolds into
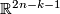 , Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
, Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Skopenkov2016e] A. Skopenkov, Embeddings just below the stable range: classification, to appear in Bull. Man. Atl.
- [Skopenkov2019] A. Skopenkov, A short exposition of the Levine-Lidman example of spineless 4-manifolds. Available at the arXiv:1911.07330.
- [Skopenkov2022] A. Skopenkov, Invariants of embeddings of 2-surfaces in 3-space. Available at the arXiv:2201.10944.
- [Tonkonog2010] D. Tonkonog, Embedding punctured $n$-manifolds in Euclidean $(2n-1)$-space
- [Vrabec1989] J. Vrabec, Deforming a PL Submanifold of Euclidean Space into a Hyperplane., Trans. Am. Math. Soc. 312 (1989), 155-78.
- [Wall1964a] C. T. C. Wall, Differential topology, IV (theory of handle decompositions), Cambridge (1964), mimeographed notes.
- [Wall1965] C. T. C. Wall, Unknotting tori in codimension one and spheres in codimension two., Proc. Camb. Philos. Soc. 61 (1965), 659-664. MR0184249 (32 #1722) Zbl 0135.41602
- [Wall1966] C. T. C. Wall, Classification problems in differential topology. V. On certain
 -manifolds, Invent. Math. 1 (1966), 355-374; corrigendum, ibid 2 (1966), 306. MR0215313 (35 #6154) Zbl 0149.20601
-manifolds, Invent. Math. 1 (1966), 355-374; corrigendum, ibid 2 (1966), 306. MR0215313 (35 #6154) Zbl 0149.20601
- [Zeeman1963] E. C. Zeeman, Seminar on Combinatorial Topology, IHES, 1963 (revised 1966).