2-manifolds
|
The user responsible for this page is Daniel Müllner. No other user may edit this page at present. |
Contents |
1 Introduction
A surface is a synonym for a  -dimensional manifold. Complex
-dimensional manifold. Complex  -dimensional (real
-dimensional (real  -dimensional) complex manifolds are also called surfaces. This article deals with real, compact, connected surfaces. Unless stated otherwise (Sections 2 and 3), surfaces without boundary are considered.
-dimensional) complex manifolds are also called surfaces. This article deals with real, compact, connected surfaces. Unless stated otherwise (Sections 2 and 3), surfaces without boundary are considered.
2 First construction: connected sum
2.1 Orientable surfaces
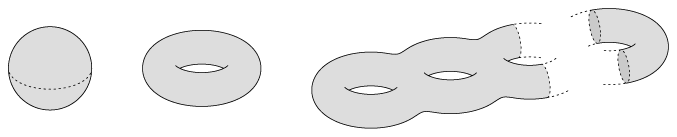
The two simplest closed orientable  -manifolds are:
-manifolds are:
- the
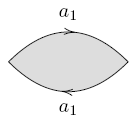
 -sphere:
-sphere: 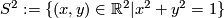 ,
,
- the
 -torus:
-torus: 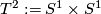 , the Cartesian product of two circles.
, the Cartesian product of two circles.
All orientable surfaces are homeomorphic to the connected sum of  tori
tori 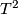 (
(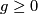 ) and so we define
) and so we define
-
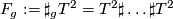 , the
, the  -fold connected sum of the
-fold connected sum of the  -torus.
-torus.
The case 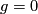 refers to the 2-sphere
refers to the 2-sphere  . The number
. The number  is called the genus of the surface: for more on the concept of genus see, e.g. [Hirzebruch&Kreck2009].
is called the genus of the surface: for more on the concept of genus see, e.g. [Hirzebruch&Kreck2009].
2.2 Non-orientable surfaces
The simplest non-orientable surface is the real projective plane 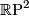 : for the history of the discovery of this interesting manifold see the page Projective plane: a history.
: for the history of the discovery of this interesting manifold see the page Projective plane: a history.
All non-orientable surfaces are homeomorphic to the connected sum of  real projective planes and and so for all
real projective planes and and so for all 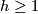 we define
we define
-
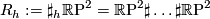 , to be the
, to be the  -fold connected sum of
-fold connected sum of 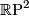 .
.
For example, the Klein bottle is homeomorphic to 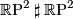 . The number
. The number  is called the genus or cross-cap number of the surface.
is called the genus or cross-cap number of the surface.

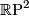 in
in 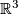 . This steel sculpture stands in front of the Oberwolfach Institute.
. This steel sculpture stands in front of the Oberwolfach Institute.3 Surfaces with boundary
The boundary of a surface is a disjoint union (possibly empty) of circles. Surfaces with boundary can be constructed by removing open discs from surfaces without boundary.
4 Classification
Compact, connected surfaces are classified by orientability (yes/no), the number of boundary components (a nonnegative integer) and the genus after filling the bounday circles by disks (an integer 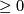 in the orientable case,
in the orientable case, 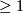 in the non-orientable case). Instead of the genus, also e. g. the Euler characteristic can be used in the classification. The classifications up to homotopy equivalence, homeomorphism, PL-equivalence and diffeomorphism coincide.
in the non-orientable case). Instead of the genus, also e. g. the Euler characteristic can be used in the classification. The classifications up to homotopy equivalence, homeomorphism, PL-equivalence and diffeomorphism coincide.
References: [Ahlfors&Sario1960, Thm. 1.42A, 1§8], [Hirsch1994, Thm. 9.3.11], [Moise1977, Thm. 8.3, Thm. 8.5, Thm. 22.9]
The connected sum of 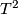 with
with 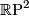 is homeomorphic to
is homeomorphic to 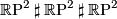 . Thus, the set of homeomorphism classes of surfaces is a commutative monoid with respect to connected sum, and is generated by
. Thus, the set of homeomorphism classes of surfaces is a commutative monoid with respect to connected sum, and is generated by 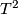 and
and
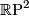 , with the sole relation
, with the sole relation 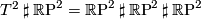 .
.
Closed 2-manifolds are homeomorphic if and only if they have isomorphic intersection forms. Likewise, compact 2-manifolds with non-empty boundary are homeomorphic if and only if they have isomorphic intersection forms. Cf. the topological classification of simply-connected 4-manifolds.
5 More constructions
5.1 By polygons
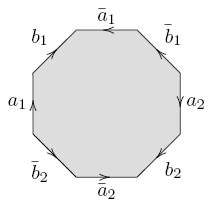
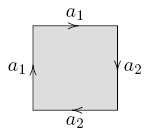
Each orientable surface of genus  can be constructed by identifying pairs of edges in a regular polygon with
can be constructed by identifying pairs of edges in a regular polygon with 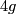 sides. Label the edges by the sequence
sides. Label the edges by the sequence 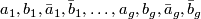 . Also orient the edges such that those labeled without an overbar are oriented in one direction (e. g. clockwise) and those with an overbar are oppositely oriented. Now identify corresponding edges, respecting the orientation.
. Also orient the edges such that those labeled without an overbar are oriented in one direction (e. g. clockwise) and those with an overbar are oppositely oriented. Now identify corresponding edges, respecting the orientation.
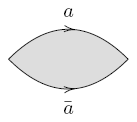
The 2-sphere can be obtained from a 2-gon with edges labeled 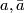 .
.
Each non-orientable surface of genus  can be obtained from a
can be obtained from a 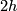 -gon with edges labeled
-gon with edges labeled 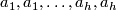 .
.
Reference: [Massey1977, Section 1.5]
5.2 By gluing handles and crosscaps
An orientable surface of genus  can be obtained by successively gluing
can be obtained by successively gluing  1-handles to the 2-sphere such that the embeddings of
1-handles to the 2-sphere such that the embeddings of 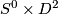 in
in 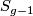 are in each case either orientation-preserving or orientation-reversing on both components
are in each case either orientation-preserving or orientation-reversing on both components 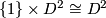 and
and 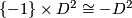 .
.
A non-orientable surface of genus  can be obtained by gluing
can be obtained by gluing  crosscaps to
crosscaps to  . For this, embed
. For this, embed 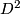 in
in  (or
(or 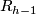 from the second crosscap on), remove the interior and glue in the Möbius strip, which also has boundary
from the second crosscap on), remove the interior and glue in the Möbius strip, which also has boundary  . The result of attaching a non-orientable handle to
. The result of attaching a non-orientable handle to  or any handle to a non-orientable surface is diffeomorphic to the surface with two additional crosscaps.
or any handle to a non-orientable surface is diffeomorphic to the surface with two additional crosscaps.
Reference: [Hirsch1994, Section 9.1]
5.3 By branched coverings
Every orientable surface of genus  can be obtained as the branched double covering of the 2-sphere with
can be obtained as the branched double covering of the 2-sphere with 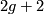 branching points.
branching points.
Proof.
The branched double covering of the 2-sphere, with 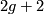 branch points, has Euler characteristic
branch points, has Euler characteristic 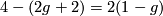 . Thus every orientable closed surface is such a branched covering.
. Thus every orientable closed surface is such a branched covering.

5.4 As complex curves
A smooth, irreducible, plane, complex projective-algebraic curve of order  (i. e. the zero set of a non-constant, homogeneous, irreducible polynomial of degree
(i. e. the zero set of a non-constant, homogeneous, irreducible polynomial of degree  in
in 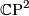 whose gradient vector does not vanish in any point of the zero set) is a compact, connected, orientable, real surface of genus
whose gradient vector does not vanish in any point of the zero set) is a compact, connected, orientable, real surface of genus
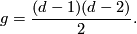
Furthermore, surfaces of every degree can be obtained as normalizations of plane, complex projective-algebraic curves with only double points as singularities.
Reference: [Brieskorn&Knörrer1986, Lemma 9.2.1]
6 Properties
6.1 Orientable surfaces
Let 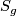 denote an oriented surface of genus
denote an oriented surface of genus  .
.
- By the polygon construction above, each orientable surface has a cell decomposition with one 0-cell,
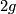 1-cells and one 2-cell. All differentials in the chain complex are zero maps.
1-cells and one 2-cell. All differentials in the chain complex are zero maps.
- Therefore, the homology groups with any coefficients
 are given by
are given by 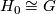 ,
, 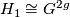 ,
, 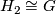 .
.
- The integral cohomology ring is completely determined by the intersection form on
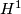 , which is necessarily isomorphic to the hyperbolic form. A basis for
, which is necessarily isomorphic to the hyperbolic form. A basis for 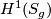 , for which the intersection form is the standard hyperbolic form, is given by the loops
, for which the intersection form is the standard hyperbolic form, is given by the loops  in the polygon construction above.
in the polygon construction above.
- Homotopy groups
- For the homotopy group of
 , see the article about spheres.
, see the article about spheres.
- All surfaces of higher genus
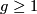 are aspherical with fundamental group
are aspherical with fundamental group 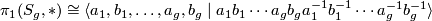 . In particular, the fundamental group of the 2-torus is isomorphic to the abelian group
. In particular, the fundamental group of the 2-torus is isomorphic to the abelian group 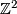 .
.
- For the homotopy group of
- All orientable surfaces can be embedded in
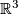 .
.
- Every surface can be given a complex structure. Together with the complex structure, it is a Riemann surface
- Characteristic classes
- All Stiefel-Whitney classes vanish.
- All Pontrjagin classes vanish.
- The Euler characteristic is
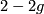 .
.
- Given a complex structure on the surface, the first Chern class is equal to the Euler class.
- All orientable surfaces admit metrics with constant curvature: the standard metric on the unit sphere in
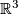 has constant positive curvature, the torus can be given a flat metric, and all surfaces of higher genus admit metrics of constant negative curvature.
has constant positive curvature, the torus can be given a flat metric, and all surfaces of higher genus admit metrics of constant negative curvature.
- All surfaces are smoothly amphicheiral.
6.2 Non-orientable surfaces
Let 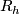 denote an non-orientable surface of genus
denote an non-orientable surface of genus  .
.
- Again, each non-orientable surface has a cell decomposition with one 0-cell,
 1-cells and one 2-cell. The differential
1-cells and one 2-cell. The differential 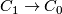 is the zero map, while the differential
is the zero map, while the differential 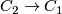 with respect to the basis given by the loops the loops
with respect to the basis given by the loops the loops 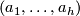 in the polygon construction is the matrix
in the polygon construction is the matrix  .
.
- Therefore, the integral homology groups are isomorphic to
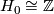 ,
, 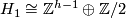 ,
, 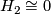 .
.
- The mod-2 homology groups are
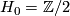 ,
, 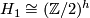 ,
, 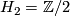 since the chain complex above is acyclic mod 2. The intersection form on
since the chain complex above is acyclic mod 2. The intersection form on 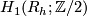 with respect to this cellular basis is given by the identity matrix.
with respect to this cellular basis is given by the identity matrix.
- Homotopy groups
- The fundamental group of
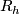 is
is 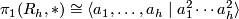 .
.
- The orientation double covering of
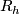 is
is 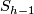 . Therefore, all higher homotopy groups of
. Therefore, all higher homotopy groups of 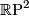 equal those of
equal those of  , and the non-orientable surfaces of higher genus are aspherical.
, and the non-orientable surfaces of higher genus are aspherical.
- The fundamental group of
- The orientation double covering also determines the curvature properties:
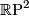 can be given a metric with constant positive curvature, the Klein bottle a flat metric, and all nonorientable surfaces can be given metrics with constant negative curvature.
can be given a metric with constant positive curvature, the Klein bottle a flat metric, and all nonorientable surfaces can be given metrics with constant negative curvature.
- Non-orientable surfaces cannot be embedded in
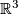 . However, they do embed in
. However, they do embed in 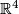 .
.
- Characteristic classes
- The first Stiefel-Whitney class is the orientation character. It can be described by the homomorphism
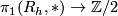 which maps each generator
which maps each generator 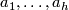 to the generator of
to the generator of 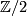 . The second Stiefel-Whitney class is zero if
. The second Stiefel-Whitney class is zero if  is even and is the non-zero element of
is even and is the non-zero element of 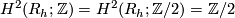 if
if  is odd. In all cases
is odd. In all cases 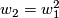 .
.
- The Euler characteristic is
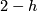 .
.
- The first Stiefel-Whitney class is the orientation character. It can be described by the homomorphism
6.3 General
There are purely point-set topology characterizations of surfaces; see [Wilder1949].
7 References
- [Ahlfors&Sario1960] L. V. Ahlfors and L. Sario, Riemann surfaces, Princeton University Press, Princeton, N.J., 1960. MR0114911 (22 #5729) Zbl 0508.01017
- [Brieskorn&Knörrer1986] E. Brieskorn and H. Knörrer, Plane algebraic curves, Birkhäuser Verlag, Basel, 1986. MR886476 (88a:14001) Zbl 0588.14019
- [Hirsch1994] M. W. Hirsch, Differential topology, Springer-Verlag, New York, 1994. MR1336822 (96c:57001) Zbl 0804.57001
- [Hirzebruch&Kreck2009] F. E. P. Hirzebruch and M. Kreck, On the concept of genus in topology and complex analysis, Notices Amer. Math. Soc. 56 (2009), no.6, 713–719. MR2536790 (2010h:57030) Zbl 1171.57300
- [Massey1977] W. S. Massey, Algebraic topology: an introduction, Springer-Verlag, New York, 1977. MR0448331 (56 #6638) Zbl 0725.55001
- [Moise1977] E. E. Moise, Geometric topology in dimensions
 and
and  , Springer-Verlag, New York, 1977. MR0488059 (58 #7631) Zbl 0349.57001
, Springer-Verlag, New York, 1977. MR0488059 (58 #7631) Zbl 0349.57001
- [Wilder1949] R. L. Wilder, Topology of Manifolds, American Mathematical Society, 1949. MR0598636 (82a:57001) Zbl 0511.57001
8 External links
- The Wikipedia page about surfaces