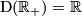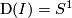1-manifolds
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 08:32, 18 July 2013 and the changes since publication. |
|
The user responsible for this page is Oleg Viro. No other user may edit this page at present. |
1 Introduction
According to the general definition of manifold, a manifold of dimension 1 is a topological space which is second countable (i.e., its topological structure has a countable base), satisfies the Hausdorff axiom (any two different points have disjoint neighborhoods) and each point of which has a neighbourhood homeomorphic either to the real line  or to the half-line
or to the half-line 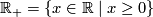 .
.
Manifolds of dimension 1 are called curves, but this name may lead to a confusion, because many mathematical objects share it. Even in the context of topology, the term curve may mean not only a manifold of dimension 1 with an additional structure, but, for instance, an immersion of a smooth manifold of dimension 1 to Euclidean space  . To be on the safe side, we use an unambiguous term manifold of dimension
. To be on the safe side, we use an unambiguous term manifold of dimension  or
or  -manifold.
-manifold.
The material presented below is not well represented in the literature. This happened, probably, because it is considered too simple. It was difficult to find appropriate references. The proofs are really elementary, but use ideas that are barely applicable in similar high-dimensional situations. That's why most the results below are provided with proofs.
Besides the adjacent field of dynamics, there is no research activity related to the topology of 1-manifolds. The dynamical topics have been left outside the scope of this text. In particular, no infinite group actions are considered, although actions of finite groups on 1-manifolds are on this side of the natural borderline, and a complete account of them is presented.
For other expositions about  -manifolds, see [Ghys2001], [Gale1987] and also [Fuks&Rokhlin1984, Sections 3.1.1.16-19].
-manifolds, see [Ghys2001], [Gale1987] and also [Fuks&Rokhlin1984, Sections 3.1.1.16-19].
2 Construction and examples
2.1 Examples of connected 1-manifolds
- The real line:
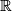
- The half-line:
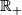
- The circle:
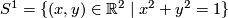
- The closed interval:
![I=[0,1]](/images/math/1/c/a/1ca01533a825141b051c7492a6fa6427.png)
2.2 Doubling
If  is an
is an  -manifold and
-manifold and 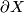 is its boundary (i.e., the set of points of
is its boundary (i.e., the set of points of  that do not have neighborhoods homeomorphic to the Euclidean space
that do not have neighborhoods homeomorphic to the Euclidean space  ), then the quotient of the disjoint union
), then the quotient of the disjoint union  of two copies of
of two copies of  by the identity map
by the identity map
 is an
is an  -manifold with empty boundary, called the double of
-manifold with empty boundary, called the double of  and denoted by
and denoted by 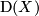 .
.
This operation is well defined up to homeomorphism. It gives a natural embedding of a manifold with boundary into a manifold without boundary (i.e., with empty boundary) and allows one to reduce many problems about manifolds with boundary to problems about manifolds without boundary.
Examples:
3 Topological classification
3.1 Reduction to classification of connected manifolds
The following elementary facts hold for  -manifolds of any dimension
-manifolds of any dimension  :
:
Any manifold is homeomorphic to the disjoint sum of its connected components.
A connected component of an  -manifold is a
-manifold is a  -manifold.
-manifold.
Two manifolds are homeomorphic iff there exists a one-to-one correspondence between their components such that the corresponding components are homeomorphic.
3.2 Topological classification of connected 1-manifolds
Theorem 3.1.
Any connected  -manifold is homeomorphic to one of the following four manifolds:
-manifold is homeomorphic to one of the following four manifolds:
- real line
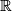 ,
,
- half-line
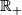 ,
,
- circle
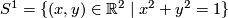 ,
,
- closed interval
![I=[0,1]](/images/math/1/c/a/1ca01533a825141b051c7492a6fa6427.png) .
.
No two of these manifolds are homeomorphic to each other.
3.3 Characterizing the topological type of a connected 1-manifold
Theorem 3.2.
- Any connected non-compact
 -manifold without boundary is homeomorphic to
-manifold without boundary is homeomorphic to  .
.
- Any connected non-compact
 -manifold with non-empty boundary is homeomorphic to
-manifold with non-empty boundary is homeomorphic to  .
.
- Any connected closed
 -manifold is homeomorphic to
-manifold is homeomorphic to  .
.
- Any connected compact
 -manifold with non-empty boundary is homeomorphic to
-manifold with non-empty boundary is homeomorphic to  .
.
Thus, for connected 1-manifolds, two invariants, compactness and presence of boundary, form a complete system of topological invariants. Each of the invariants takes two values.
Theorems 3.1 and 3.2 above solve the topological classification problem for 1-manifolds in the most effective way that one can desire. Surprisingly, many Topology textbooks manage not to mention this fundamental result.
3.4 About proofs of the classification theorems
The proofs of Theorems 3.1 and 3.2 above are elementary. They can be found, e.g., in [Fuks&Rokhlin1984, Sections 3.1.1.16-19] and [Gale1987]. In the case of 1-manifolds without boundary, the proofs are based on the following simple lemmas:
Lemma 3.3. Any connected  -manifold covered by two open sets homeomorphic to
-manifold covered by two open sets homeomorphic to  is homeomorphic either to
is homeomorphic either to  or to
or to  .
.
Under assumptions of Lemma 3.3, the 1-manifold is homeomorphic to  iff the intersection of two open sets is connected, and it is homeomorphic to
iff the intersection of two open sets is connected, and it is homeomorphic to  iff the intersection consists of two connected components (the intersection cannot have more than two components).
iff the intersection consists of two connected components (the intersection cannot have more than two components).
Lemma 3.4. If a topological space  can be represented as the union of a nondecreasing sequence of open subsets, all homeomorphic to
can be represented as the union of a nondecreasing sequence of open subsets, all homeomorphic to  , then
, then  is homeomorphic to
is homeomorphic to  .
.
From the topological classification for 1-manifolds without boundary, the classification for 1-manifolds with non-empty boundary is obtained using the doubling operation, see Section 2.2 above.
3.5 Corollary: homotopy classification
Theorem 3.5.
Each connected  -manifold is either contractible, or homotopy equivalent to circle.
-manifold is either contractible, or homotopy equivalent to circle.
This follows immediately from Theorem 3.1.
3.6 Corollary: Cobordant 0-manifolds
Theorem 3.6.
A compact  -manifold
-manifold  bounds a compact
bounds a compact  -manifold iff the number of points in
-manifold iff the number of points in  is even.
is even.
Corollary 3.7.
Two compact  -manifolds are cobordant iff their numbers of points are congruent modulo
-manifolds are cobordant iff their numbers of points are congruent modulo  .
.
3.7 Characterizing connected 1-manifolds in terms of separating points
A subset  of a topological space
of a topological space  is said to separate
is said to separate  if
if 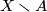 can be presented as a
union of two disjoint open sets.
can be presented as a
union of two disjoint open sets.
Theorem 3.8. (See [Moore1920].)
Let  be a connected compact Hausdorff second countable topological space.
be a connected compact Hausdorff second countable topological space.
- If every two points separate
 , then
, then  is homeomorphic to the circle.
is homeomorphic to the circle.
- If each point, with two exceptions, separates
 , then
, then  is homeomorphic to
is homeomorphic to  .
.
Any point 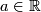 splits
splits  to two disjoint open rays
to two disjoint open rays 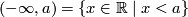 and
and 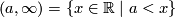 .
.
Theorem 3.9. (See [Ward1936].)
Let  be a connected locally compact Hausdorff second countable topological space.
be a connected locally compact Hausdorff second countable topological space.
- If the complement of each point in
 consists of two connected components, then
consists of two connected components, then  is homeomorphic to
is homeomorphic to  .
.
- If
 contains a point
contains a point  such that
such that 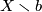 is connected and
is connected and 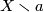 consists of two connected components for each
consists of two connected components for each 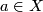 ,
, 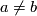 , then
, then  is homeomorphic to
is homeomorphic to  .
.
4 Orders and orientations
4.1 Interval topology
Most properties specific for 1-manifolds can be related to the fact that the topological structure on a connected 1-manifold is defined by linear or cyclic ordering of its points.
Open intervals 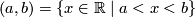 form a base of the standard topology on
form a base of the standard topology on  . This way of introducing a topological structure can be applied in any (linearly) ordered set
. This way of introducing a topological structure can be applied in any (linearly) ordered set  (though in a general linearly ordered set one should include into the base, together with open intervals
(though in a general linearly ordered set one should include into the base, together with open intervals 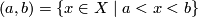 , also open rays
, also open rays 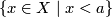 and
and 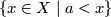 ). On
). On  and
and  , the standard topology is induced from the standard topology on
, the standard topology is induced from the standard topology on  , and can be described in terms of the order.
, and can be described in terms of the order.
Theorem 4.1.
Every connected non-closed  -manifold admits exactly two linear orders defining its topology.
-manifold admits exactly two linear orders defining its topology.
Proof.
A linear order 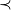 on a set
on a set  is encoded in the system of rays
is encoded in the system of rays 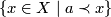 for
for 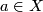 .
.
By Theorem 3.2, a connected non-closed 1-manifold is homeomorphic either to  , or
, or  , or
, or  . On each of these 1-manifolds there are two linear orders,
. On each of these 1-manifolds there are two linear orders,  and
and  , defining the topology. For these orders, the rays
, defining the topology. For these orders, the rays 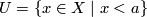 and
and 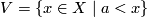 are defined by the topology: they are just the connected components of
are defined by the topology: they are just the connected components of 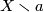 .
.
For any other linear order 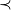 defining the same topology on
defining the same topology on  , the rays
, the rays 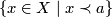 and
and 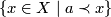 are open and intersect the connected components
are open and intersect the connected components  and
and  of
of 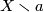 in disjoint open sets. By connectedness of
in disjoint open sets. By connectedness of  and
and  , one of them coincides with
, one of them coincides with  , the other with
, the other with  . Hence,
. Hence, 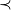 coincides with one of the standard orders, either with
coincides with one of the standard orders, either with  , or
, or  .
.

4.2 Orientations
An orientation of a 1-manifold can be interpreted via linear orderings on its open subsets homeomorphic to  or
or  .
An orientation of
.
An orientation of  or
or  is nothing but one of the two linear orders defining the topological structure.
is nothing but one of the two linear orders defining the topological structure.
Relation to the general homological definition of orientation.
Recall that in high dimensional situations orientation of an open set 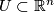 is defined as a coherent choice of generators in homology groups
is defined as a coherent choice of generators in homology groups 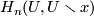 for
for 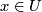 . In our case
. In our case  and the group
and the group 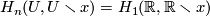 is generated by a homology class of a singular cycle consisting of a single singular 1-simplex
is generated by a homology class of a singular cycle consisting of a single singular 1-simplex 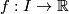 , which is an embedding with
, which is an embedding with 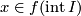 . There are two generators: one is represented by a monotone increasing
. There are two generators: one is represented by a monotone increasing  , another, by a monotone decreasing
, another, by a monotone decreasing  . A choice of linear order on
. A choice of linear order on  allows one to distinguish one of the generators of
allows one to distinguish one of the generators of 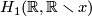 : namely, the one represented by
: namely, the one represented by  which is monotone increasing with respect to the order chosen on
which is monotone increasing with respect to the order chosen on  .
.
For extending the notion of orientation to a general 1-manifold, one needs to globalize the idea of linear order. It can be done in several ways.
For example, due to the topological classification, one can restrict to just four model 1-manifolds:  ,
,  ,
,  and
and  . For
. For  ,
,  and
and  , an orientation still can be defined as a linear order determining the topology of the manifold. For
, an orientation still can be defined as a linear order determining the topology of the manifold. For  this approach does not work, but can be adjusted: instead of linear order one can rely on cyclic orders that define the topology. However, this is a bit awkward, as cyclic orders are more cumbersome than usual linear orders.
this approach does not work, but can be adjusted: instead of linear order one can rely on cyclic orders that define the topology. However, this is a bit awkward, as cyclic orders are more cumbersome than usual linear orders.
There is a more conceptual approach, which imitates the classical definition of orientations of differentiable manifolds, but relies, instead of coordinate charts, on local linear orders.
Let  be a 1-manifold. A local order of
be a 1-manifold. A local order of  is a pair consisting of an open set
is a pair consisting of an open set 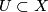 homeomorphic to
homeomorphic to  or
or  and a linear order on
and a linear order on  defining the topology on
defining the topology on  . Two local orders
. Two local orders 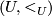 ,
, 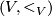 are said to agree if on any connected component
are said to agree if on any connected component  of
of  the orders
the orders 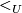 and
and 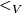 induce the same order.
induce the same order.
Denote by 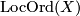 the set of all local orders of
the set of all local orders of  .
An orientation on
.
An orientation on  is a map
is a map 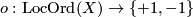 such that for any
such that for any 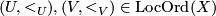 and the restrictions of
and the restrictions of 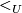 and
and 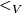 to any connected component of
to any connected component of  coincide if
coincide if 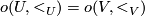 and do not coincide if
and do not coincide if 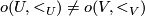 .
.
Obvious Lemma 4.2. Let 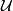 be a collection of open sets in a
be a collection of open sets in a  -manifold X homeomorphic to
-manifold X homeomorphic to  and let for any open set
and let for any open set  homeomorphic to
homeomorphic to  or
or  there exist
there exist 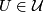 such that
such that  is connected. If each
is connected. If each 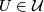 is equipped with a linear order
is equipped with a linear order 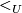 defining the topology on
defining the topology on  such that the local orders
such that the local orders 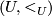 and
and 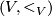 agree for any
agree for any 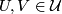 , then there exists a unique orientation
, then there exists a unique orientation  on
on  such that
such that 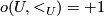 for any
for any 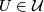 . Moreover any orientation on
. Moreover any orientation on  comes from such coherent linear orders
comes from such coherent linear orders 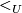 on all elements of
on all elements of 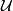 .
.
Theorem 4.3.
On any connected  -manifold there exists exactly two orientations.
-manifold there exists exactly two orientations.
Proof. If  is a non-closed connected 1-manifold, then for
is a non-closed connected 1-manifold, then for 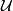 satisfying the hypothesis of Lemma 4.2 we can take a collection consisting of a single element
satisfying the hypothesis of Lemma 4.2 we can take a collection consisting of a single element 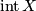 . If
. If  is closed connected 1-manifold, then for
is closed connected 1-manifold, then for 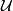 we can take the collection of complements of single points. Then the intersection
we can take the collection of complements of single points. Then the intersection  for any
for any 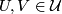 consists of two connected components homeomorphic to
consists of two connected components homeomorphic to  . We can choose stereographic projections as homeomorphisms of them to
. We can choose stereographic projections as homeomorphisms of them to  in such a way that the transition mapping from one of these charts to another one is
in such a way that the transition mapping from one of these charts to another one is 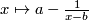 . It is monotone increasing on each of the rays
. It is monotone increasing on each of the rays 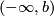 and
and 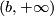 . Therefore the orders obtained on complements of points via these stereographic projections from the standard order
. Therefore the orders obtained on complements of points via these stereographic projections from the standard order  on
on  agree with each other and we can apply Lemma 4.2.
agree with each other and we can apply Lemma 4.2.

Corollary 4.4.
Any  -manifold admits an orientation. If a
-manifold admits an orientation. If a  -manifold consists of
-manifold consists of  connected components, then it admits exactly
connected components, then it admits exactly 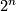 orientations.
orientations.
4.3 Self-homeomorphisms
Theorem 4.5.
A map 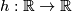 is a homeomorphism iff
is a homeomorphism iff  is a monotone bijection.
is a monotone bijection.
Proof. Let 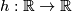 be a homeomorphism. First, observe that
be a homeomorphism. First, observe that  maps every ray to a ray. Indeed,
for any
maps every ray to a ray. Indeed,
for any 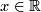 , the map
, the map  induces a homeomorphism
induces a homeomorphism 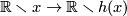 .
The rays
.
The rays 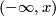 and
and 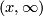 are connected components of
are connected components of 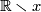 .
Therefore their images are connected components
.
Therefore their images are connected components 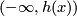 and
and 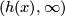 of
of 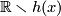 .
.
Observe that rays have the same direction iff one of them is contained in the other one. Therefore two rays of the same direction are mapped by  to rays with the same direction. Thus rays
to rays with the same direction. Thus rays 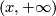 are mapped either all to rays
are mapped either all to rays 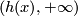 or all to
or all to 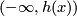 . Thus
. Thus  is monotone.
is monotone.
Let 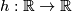 be a monotone bijection. Then the image and preimage under
be a monotone bijection. Then the image and preimage under  of any open interval are open intervals. Therefore, both
of any open interval are open intervals. Therefore, both  and
and 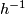 are continuous, and hence
are continuous, and hence  is a homeomorphism.
is a homeomorphism.

The following theorem can be proved similarly or can be deduced from Theorem 4.5.
Theorem 4.6.
- A map
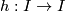 is a homeomorphism iff
is a homeomorphism iff  is a monotone bijection.
is a monotone bijection.
- A map
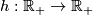 is a homeomorphism iff
is a homeomorphism iff  is a monotone increasing bijection.
is a monotone increasing bijection.
- A map
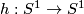 is a homeomorphism iff
is a homeomorphism iff  is a bijection that either preserves or reverses the cyclic order of points on
is a bijection that either preserves or reverses the cyclic order of points on  .
.
A self-homeomorphism 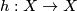 of a connected 1-manifold maps an orientation
of a connected 1-manifold maps an orientation
 of
of  to some orientation, which is either
to some orientation, which is either  or
or 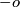 (as a connected
1-manifold,
(as a connected
1-manifold,  has just these two orientations). Whether
has just these two orientations). Whether  maps
maps  to itself
or to the opposite orientation
to itself
or to the opposite orientation 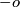 does not depend on
does not depend on  : it maps
: it maps  to
to  iff it maps
iff it maps 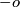 to
to 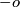 . We say that
. We say that  is orientation preserving if
it maps any orientation of
is orientation preserving if
it maps any orientation of  to itself and orientation reversing if
if it maps any orientation of
to itself and orientation reversing if
if it maps any orientation of  to the opposite orientation.
to the opposite orientation.
The half-line  does not admit a self-homeomorphism reversing orientation. Any connected 1-manifold non-homeomorphic to
does not admit a self-homeomorphism reversing orientation. Any connected 1-manifold non-homeomorphic to  admits an orientation reversing map. Thus,
admits an orientation reversing map. Thus,  is chiral and connected 1-manifolds non-homeomorphic to
is chiral and connected 1-manifolds non-homeomorphic to  are amphicheiral.
are amphicheiral.
Thus, there are 5 topological types of oriented connected 1-manifolds: the topological type of the non-oriented half-line splits into the oriented topological types of  and
and 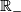 with the orientations induced by the standard order.
with the orientations induced by the standard order.
5 Invariants
5.1 Basic invariants
As follows from the Theorems 3.1 and 3.2 above, the following invariants:
- the number of connected components,
- the compactness of each connected component,
- and the number of boundary points of each connected component,
determine the topological type of a 1-manifold.
5.2 Homology groups
The low dimensional homology groups of 1-manifolds are presented in the following table:
| Homology group \ 1-manifold | 
|

|

|

|
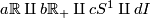
|
|---|---|---|---|---|---|
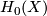
|

|

|

|

|
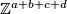
|
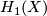
|

|

|

|

|
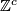
|
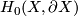
|

|

|

|

|
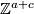
|
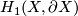
|

|

|

|

|
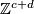
|
It is clear from the last column of this table that the absolute and relative homology groups of dimensions 1 and 2 determine the topological type of 1-manifold. Of course, the basic invariants considered above do the job in a more elementary way.
Above by homology we mean homology with compact support. For homology with closed support (Borel-Moore homology) see the following table:
| Borel-Moore homology group \ 1-manifold | 
|

|

|

|
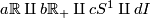
|
|---|---|---|---|---|---|
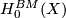
|

|

|

|

|
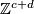
|
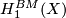
|

|

|

|

|
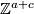
|
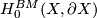
|

|

|

|

|
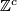
|
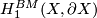
|

|

|

|

|
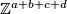
|
An orientation of a 1-manifold  gives rise to the fundamental class of
gives rise to the fundamental class of  , which belongs to
, which belongs to 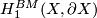 .
Cap-product by this class defines various versions of the Poincaré duality isomorphisms between usual cohomology
(recall that the usual cohomology has closed support) and the relative
Borel-Moore homology of the complementary dimension. So there are isomorphisms
.
Cap-product by this class defines various versions of the Poincaré duality isomorphisms between usual cohomology
(recall that the usual cohomology has closed support) and the relative
Borel-Moore homology of the complementary dimension. So there are isomorphisms
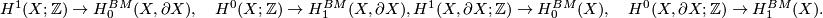
A local coefficient system on a 1-manifold homeomorphic to the circle, may be non-trivial. E.g., if the local coefficient system over  with fibre
with fibre
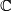 has non-trivial monodromy, then all the homology groups are trivial.
has non-trivial monodromy, then all the homology groups are trivial.
5.3 Euler characteristics
The Euler characteristic of  is 1. The Euler characteristic of
is 1. The Euler characteristic of  is 0.
is 0.
Any closed 1-manifold has Euler characteristic 0. The Euler characteristic of any compact 1-manifold is half the number of its boundary points.
When it comes to non-compact spaces, the notion of Euler characteristic becomes ambiguous.
A non-compact space has many Euler characteristics. The notion of Euler characteristic depends
on the properties that one wants to preserve. If one wants to have invariance under homotopy equivalences,
then the additivity would be lost. If one wants to keep additivity, then it is not the alternating sum of Betti numbers. If one wants to keep topological invariance and additivity, then
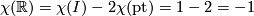 , similarly
, similarly 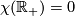 .
.
For not necessarily compact 1-manifolds probably most useful is the Euler characteristic which is defined as the alternating sum of the ranks of homology groups with closed support (Borel-Moore homology). It is additive and a topological invariant. The only property which may confuse a person with purely compact experience is that it is not homotopy invariant. With this Euler characteristic, 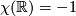 and
and 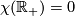 .
.
5.4 Other homotopy invariants
The homotopy invariants of 1-manifolds are extremely simple. All homology and homotopy groups of dimensions 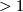 are trivial. The fundamental group
are trivial. The fundamental group
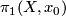 is an infinite cyclic group, if the connected component of
is an infinite cyclic group, if the connected component of  containing
containing 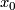 is homeomorphic to circle, and trivial otherwise.
is homeomorphic to circle, and trivial otherwise.
5.5 Tangent bundle invariants
The tangent bundles of 1-manifolds are trivial. Thus all the characteristic classes are trivial.
6 Additional structures
6.1 Triangulations
A triangulation of a 1-manifold  is a locally finite
cover of
is a locally finite
cover of  by subspaces homeomorphic to
by subspaces homeomorphic to  , any two of which have disjoint interiors and at most one common point.
The subspaces are assumed to be equipped with affine structure or, rather,
with homeomorphisms to
, any two of which have disjoint interiors and at most one common point.
The subspaces are assumed to be equipped with affine structure or, rather,
with homeomorphisms to  . The subspaces are called edges or
. The subspaces are called edges or
 -simplices, the
images of the endpoints of
-simplices, the
images of the endpoints of  are called vertices or
are called vertices or  -simplices.
-simplices.
Any 1-manifold admits a triangulation. A triangulation of a non-compact connected 1-manifold is unique up to homeomorphism.
A compact 1-manifold has non-homeomorphic triangulations, but they are easy to classify up to homeomorphism.
On the circle the topological type of a triangulation is defined by the number of 1-simplices. This number can take
any integral value 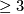 . Similarly, the topological type of a triangulation of
. Similarly, the topological type of a triangulation of  is defined by the number of 1-simplices, which can take any positive integral value.
is defined by the number of 1-simplices, which can take any positive integral value.
6.2 Metrics and intrinsic metrics
Recall that any manifold is metrizable. On a connected manifold, a metric defining its topology can be replaced by
an intrinsic metric defining the same topology. (Recall that a metric on a path-connected space is said to be intrinsic if the distance between any two points is equal to the infimum of lengths of paths connecting the points, and that the length of a path 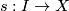 in a metric space
in a metric space  with metric
with metric 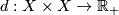 is
is
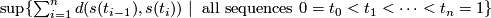 .)
.)
A connected 1-manifold with an intrinsic metric is defined up to isometry by the diameter of the space. Recall that the diameter of a metric space  with metric
with metric 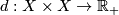 is
is 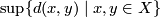 .
.
For each value of the diameter and each homeomorphism type of a connected 1-manifold with intrinsic metric there is a unique standard model:
Theorem 6.1.
A  -manifold
-manifold  with intrinsic metric and diameter
with intrinsic metric and diameter 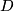 is isometric to
is isometric to
-
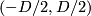 with the metric induced from the standard metric on
with the metric induced from the standard metric on  and any
and any ![D\in(0,\infty]](/images/math/a/9/8/a98f21564b6d664f43fa7a6b0614ea3a.png) ;
;
-
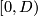 with the metric induced from the standard metric on
with the metric induced from the standard metric on  and any
and any ![D\in(0,\infty]](/images/math/a/9/8/a98f21564b6d664f43fa7a6b0614ea3a.png) ;
;
- the circle
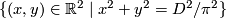 with the intrinsic metric defined by the lengths of paths on the circle measured in
with the intrinsic metric defined by the lengths of paths on the circle measured in 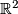 and any
and any 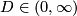 ;
;
-
![[0,D]](/images/math/9/2/b/92beb9ea7237e94d7250de8c44fa6175.png) with the metric induced from the standard metric on
with the metric induced from the standard metric on  and any
and any 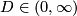 .
.
The isometries to the standard models can be constructed using distances from some points. For example, for a connected 1-manifold  homeomorphic
to
homeomorphic
to  equipped with an intrinsic metric, the distance to the only boundary point defines a canonical isometry
equipped with an intrinsic metric, the distance to the only boundary point defines a canonical isometry 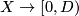 .
.
6.3 Smooth structures
Theorem 6.2.
Any  -manifold admits a smooth structure of any class
-manifold admits a smooth structure of any class  .
.
Proof. A smooth structure can be induced by the isometry to the corresponding standard model from Theorem 6.1 above.

If smooth 1-manifolds  and
and  are homeomorphic, then they are also diffeomorphic. Moreover,
are homeomorphic, then they are also diffeomorphic. Moreover,
Theorem 6.3.
Any homeomorphism between two smooth  -manifolds can be approximated in the
-manifolds can be approximated in the 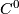 -topology by a diffeomorphism.
-topology by a diffeomorphism.
Proof. By Theorems 4.5 and 4.6, a homeomorphism is monotone in the appropriate sense. Choose a net of points in the source such that the image of each of them is sufficiently close to the images of its neighbors. Take a smooth monotone bijection coinciding with the homeomorphism at the chosen points.

7 Constructions
7.1 Surgery
Any compact 1-manifold can be transformed by surgeries to any other 1-manifold with the same boundary.
If two compact 1-manifolds with the same boundary are oriented and the induced orientations on the boundary coincide, then the surgery can be chosen to preserve the orientation (this means that the corresponding cobordism is an oriented 2-manifold and its orientation induces on the boundary the given orientation on one of the 1-manifolds and the orientation opposite to the given one on the other 1-manifold).
An index-1 surgery preserving orientation on a closed 1-manifold changes the number of connected components by 1. An index-1 surgery on a 1-manifold, which does not preserve every orientation, preserves the number of connected components. In particular, if an index-1 surgery on a connected 1-manifold does not preserve an orientation, then its result is a connected 1-manifold.
7.2 Connected sums
The notion of connected sum is defined for 1-manifolds, but the connectivity of the outcome is different in dimension 1 compared to other dimensions.
Indeed, the term connected sum can be misleading in dimension 1 since a connected sum
of connected 1-manifolds may be not connected. For example a connected sum of two
copies of  is a disjoint sum of two copies of
is a disjoint sum of two copies of  .
.
Note that connected sum is only a well defined operation on oriented manifolds and one has to be careful with the orientations. For example
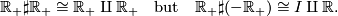
8 Groups of self-homeomorphisms
8.1 Mapping class groups
Recall that the mapping class group of a manifold  is the quotient group of the group
is the quotient group of the group 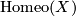 of all homeomorphisms
of all homeomorphisms 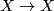 by the normal subgroup of homeomorphisms isotopic to the identity.
In other words, the mapping class group of
by the normal subgroup of homeomorphisms isotopic to the identity.
In other words, the mapping class group of  is
is  .
.
An orientation reversing homeomorphism cannot be isotopic to an orientation preserving homeomorphism. For auto-homeomorphisms of a connected 1-manifold this is the only obstruction to being isotopic:
Theorem 8.1.
Any two auto-homeomorphisms of a connected  -manifold that are either both orientation preserving, or both orientation
reversing are isotopic.
-manifold that are either both orientation preserving, or both orientation
reversing are isotopic.
This is a corollary of the following two obvious lemmas.
Lemma 8.2. On rectilinear isotopy. Let  be one of the following
be one of the following  -manifolds:
-manifolds:  ,
,  , or
, or  . Let
. Let 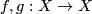 be two monotone bijections that are either both increasing or both decreasing. Then the family
be two monotone bijections that are either both increasing or both decreasing. Then the family 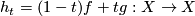 with
with ![t\in[0,1]](/images/math/4/0/d/40de672f62756d608425bb0e58f1dfa1.png) consists of monotone bijections (and hence is an isotopy between
consists of monotone bijections (and hence is an isotopy between  and
and  ).
).
Lemma 8.3. Let 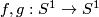 be two bijections that either both preserve or both reverse the standard
cyclic order of points on
be two bijections that either both preserve or both reverse the standard
cyclic order of points on  . Let
. Let  and
and  coincide at
coincide at 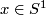 . Then
. Then  and
and  are isotopic via the canonical
isotopy which is stationary at
are isotopic via the canonical
isotopy which is stationary at  and is provided on the complement of
and is provided on the complement of  by stereographic projections and the rectilinear isotopy from Lemma 8.2 of the corresponding self-homeomorphisms of
by stereographic projections and the rectilinear isotopy from Lemma 8.2 of the corresponding self-homeomorphisms of  .
.
Corollary 8.4.
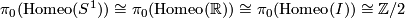 and
and
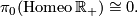
Remark. All the statements in this section remains true, if everywhere the word homeomorphism is replaced by the word diffeomorphism and  is replaced by
is replaced by 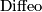 .
.
8.2 Homotopy types of groups of homeomorphisms
The group 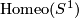 contains
contains 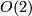 as a subgroup, which is its deformation retract. This follows from Lemma 8.3. More precisely, for each point
as a subgroup, which is its deformation retract. This follows from Lemma 8.3. More precisely, for each point 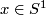 , Lemma 8.3 provides a deformation retraction
, Lemma 8.3 provides a deformation retraction 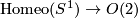 .
.
Similarly, the group of self-homeomorphisms of  isotopic to the identity contains
isotopic to the identity contains 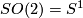 as a subgroup, which is its deformation retract.
as a subgroup, which is its deformation retract.
The groups of self-homeomorphisms of  ,
,  and
and  which are isotopic to the identity are contractible. The contraction is provided by the rectilinear isotopy from Lemma 8.2 applied to
which are isotopic to the identity are contractible. The contraction is provided by the rectilinear isotopy from Lemma 8.2 applied to 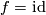 and an arbitrary
and an arbitrary  .
.
Thus for each connected 1-manifold  the group of homeomorphisms
the group of homeomorphisms 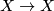 isotopic to the identity is homotopy equivalent to
isotopic to the identity is homotopy equivalent to  .
.
9 Finite group actions
9.1 The invariant intrinsic metric
Theorem 9.1.
For any effective action of a finite group  on a
on a  -manifold
-manifold  ,
there exists an intrinsic metric on
,
there exists an intrinsic metric on  invariant under this action.
invariant under this action.
Proof. Such a metric is created in three steps.
- Choose any metric
 on
on  defining the topology.
defining the topology.
- Symmetrize
 : define for any
: define for any 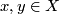 the number
the number 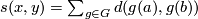 . This is a metric and it is invariant under the action.
. This is a metric and it is invariant under the action.
- Take the intrinsic metric
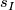 induced by
induced by  .
.

Since an intrinsic metric on a 1-manifold defines an isometry onto one of the standard models, this gives a equivariant homeomorphism to
one of the standard connected 1-manifolds with intrinsic metric and action of  by isometries.
by isometries.
9.2 Free actions
If the action of a finite group  on a 1-manifold is free, then the orbit space
on a 1-manifold is free, then the orbit space 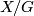 is a 1-manifold and
the natural projection
is a 1-manifold and
the natural projection 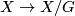 is a covering.
is a covering.
Therefore the theory of coverings gives a simple classification of free finite group actions on 1-manifolds.
A contractible 1-manifold has no non-trivial covering.
Thus, if a free finite group action on 1-manifold  has a contractible orbit space
has a contractible orbit space 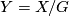 , then
, then  is a disjoint union of copies of
is a disjoint union of copies of  and
and  permutes these copies. In particular, there is no non-trivial free group action on a connected 1-manifold having contractible orbit space.
permutes these copies. In particular, there is no non-trivial free group action on a connected 1-manifold having contractible orbit space.
Coverings 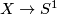 with connected
with connected  are in one-to-one correspondence with subgroups of finite indices of
are in one-to-one correspondence with subgroups of finite indices of 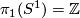 . For each
. For each 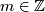 there is one subgroup with index
there is one subgroup with index  , and hence one
, and hence one  -fold covering. The total space is homeomorphic to
-fold covering. The total space is homeomorphic to  , and the covering is equivalent to
, and the covering is equivalent to 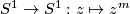 . In the corresponding action, the group is cyclic of order
. In the corresponding action, the group is cyclic of order  and acts on
and acts on  by rotations.
by rotations.
In this classification of free finite group actions on connected 1-manifolds, the orbit space plays the main role. However, it is easy to reformulate it with emphasis on the 1-manifold on which the group acts. This is done in the next two theorems.
Theorem 9.2.
There is no non-trivial free finite group action on a contractible  -manifold.
-manifold.
Theorem 9.3.
If a finite group  acts freely on the circle than
acts freely on the circle than  is cyclic. Any finite cyclic group has a linear
free action on
is cyclic. Any finite cyclic group has a linear
free action on  . Any free action of a finite cyclic group on
. Any free action of a finite cyclic group on  is conjugate to a linear action.
is conjugate to a linear action.
9.3 Asymmetry of a half-line
Theorem 9.4. There is no non-trivial action of a finite group on  .
.
Proof. We will prove that the only homeomorphism 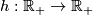 of finite order is the identity.
Observe first that any homeomorphism
of finite order is the identity.
Observe first that any homeomorphism 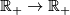 must map a boundary point to a boundary point, and hence it preserves the only boundary point
must map a boundary point to a boundary point, and hence it preserves the only boundary point 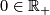 . By Theorem 9.1, there exists an intrinsic metric invariant under
. By Theorem 9.1, there exists an intrinsic metric invariant under  . Therefore,
. Therefore,  preserves the distance from the boundary point. However each point on
preserves the distance from the boundary point. However each point on  is uniquely defined by its distance to the boundary point.
is uniquely defined by its distance to the boundary point.

9.4 Actions on line and segment
Theorem 9.5.
The only orientation preserving homeomorphism 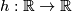 of finite order is the identity.
of finite order is the identity.
Proof. Fix a homeomorphism 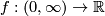 (say, define it by formula
(say, define it by formula 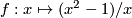 ). Consider a homeomorphism
). Consider a homeomorphism 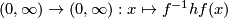 . It preserves orientation (since
. It preserves orientation (since  preserves orientation). So, it is a monotone increasing bijection
preserves orientation). So, it is a monotone increasing bijection 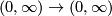 of finite order. Since it is increasing, it can be extended to
of finite order. Since it is increasing, it can be extended to  by letting
by letting 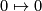 .
The extended homeomorphism has the same finite order. But by Theorem 9.4 any such homeomorphism is the identity.
.
The extended homeomorphism has the same finite order. But by Theorem 9.4 any such homeomorphism is the identity.

Theorem 9.6.
Any orientation reversing homeomorphism 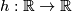 of finite order has order two. It is conjugate to the reflection in a point.
of finite order has order two. It is conjugate to the reflection in a point.
Proof. An orientation reversing homeomorphism 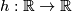 is a monotone decreasing bijection. Consider the function
is a monotone decreasing bijection. Consider the function
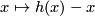 . It is also a monotone decreasing bijection
. It is also a monotone decreasing bijection 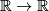 and hence there exists a unique
and hence there exists a unique 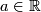 such that
such that
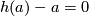 , that is
, that is 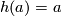 .
.
The homeomorphism  maps each connected component of
maps each connected component of 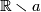 to a connected component of
to a connected component of 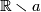 . The connected components are open rays
. The connected components are open rays 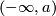 and
and 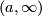 . If each of them is mapped to itself, then
. If each of them is mapped to itself, then  defines a homeomorphism of a finite order of the closed rays
defines a homeomorphism of a finite order of the closed rays ![(-\infty,a]](/images/math/8/e/1/8e1e18652b815b5ecf7a9980c1f113ce.png) and
and 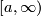 . Then by Theorem 9.4,
. Then by Theorem 9.4,  is the identity, which contradicts our assumption. Thus,
is the identity, which contradicts our assumption. Thus, ![h([a,\infty))=(-\infty,a]](/images/math/0/3/b/03b289323bdd3892f99215d55317b769.png) and
and ![h((-\infty,a])=[a,\infty)](/images/math/c/0/1/c0197d88ad2e20e88244233118e8abf7.png) . Then
. Then 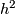 preserves the rays, and, by Theorem 9.4, is the identity. Thus
preserves the rays, and, by Theorem 9.4, is the identity. Thus  has order two.
has order two.
Choose a homeomorphism 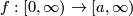 . Define function
. Define function ![g:(-\infty,0]\to(-\infty,a]](/images/math/a/5/7/a571a0efa5e39755c433cec23ee722ad.png) by the formula
by the formula 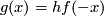 . It's a homeomorphism. Together,
. It's a homeomorphism. Together,  and
and  form a homeomorphism
form a homeomorphism 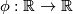 . As is easy to check,
. As is easy to check, 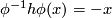 .
.

Theorem 9.7.
A non-trivial finite group acting effectively on  is a cyclic group of order
is a cyclic group of order  .
The action of the non-unit element is conjugate to the reflection in a point.
.
The action of the non-unit element is conjugate to the reflection in a point.
Proof.
As follows from Corollaries 9.5 and 9.6, any non-trivial
element of the group is an orientation reversing involution. We have to prove that the group contains at most one such element.
Assume that there are two orientation reversing homeomorphisms,  and
and  of the line
of the line  . Their composition
. Their composition 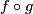 preserves orientation. Since it belongs to a finite group, it has finite order. By Theorem 9.5, it is the identity. So,
preserves orientation. Since it belongs to a finite group, it has finite order. By Theorem 9.5, it is the identity. So, 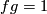 and hence
and hence 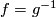 . But
. But 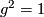 . Therefore
. Therefore 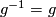 and
and 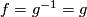 .
.

Corollary 9.8.
A non-trivial finite group acting effectively on  is a cyclic group of order
is a cyclic group of order  .
The action of the non-unit element is conjugate to the reflection in a point.
.
The action of the non-unit element is conjugate to the reflection in a point.
Proof.
Any auto-homeomorphism of  preserves the boundary and the interior of
preserves the boundary and the interior of  . Hence an effective finite group action on
. Hence an effective finite group action on  induces an action of a finite group on the interior of
induces an action of a finite group on the interior of  . An auto-homeomorphism of
. An auto-homeomorphism of  is recovered from its restriction to the interior.
Moreover, any auto-homeomorphism of
is recovered from its restriction to the interior.
Moreover, any auto-homeomorphism of 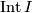 has a unique extension to an auto-homeomorphism of
has a unique extension to an auto-homeomorphism of  . The interior
. The interior 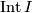 is homeomorphic to
is homeomorphic to  .
.

9.5 Actions on the circle
Theorem 9.9.
Any periodic orientation reversing homeomorphism 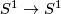 is an involution (i.e., has period
is an involution (i.e., has period  ).
It is conjugate to a reflection of
).
It is conjugate to a reflection of  in its diameter.
in its diameter.
Proof. Observe first that any orientation reversing auto-homeomorphism of the circle has a fixed point. One can prove this by elementary arguments, but we just refer to the Lefschetz Fixed Point Theorem: the Lefschetz number of such a homeomorphism is 2.
Consider the complement of a fixed point. The restriction of the homeomorphism to this complement satisfies the conditions of Theorem 9.6, which gives the required result.

Observe that by Theorems 9.6, 9.8, and 9.9 any non-identity periodic homeomorphism of a connected 1-manifold with a fixed point is an involution reversing orientation.
Theorem 9.10.
A periodic non-identity orientation preserving homeomorphism 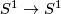 has no fixed point. It is conjugate to a rotation.
has no fixed point. It is conjugate to a rotation.
Proof. If if had a fixed point, then we could consider its restriction to the complement of this point, and by Theorem 9.5 would conclude that it is the identity and hence the whole homeomorphism is the identity.
For the same reasons, the non-identity powers of our periodic non-identity orientation preserving homeomorphism 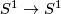 have no fixed points. Therefore, these powers form a cyclic group freely acting on
have no fixed points. Therefore, these powers form a cyclic group freely acting on  . See Theorem 9.3.
. See Theorem 9.3.

Theorem 9.11.
A finite group acting effectively on  is either cyclic or dihedral, and the action is conjugate to a linear one and extends to the standard (linear) action of the orthogonal group
is either cyclic or dihedral, and the action is conjugate to a linear one and extends to the standard (linear) action of the orthogonal group 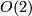 .
The standard actions of cyclic and dihedral groups on the circle are provided by the symmetry groups of regular polygons.
.
The standard actions of cyclic and dihedral groups on the circle are provided by the symmetry groups of regular polygons.
Proof.
By Theorem 9.1, for a finite group action on  there exists an invariant intrinsic metric. By Theorem 6.1, with this metric
there exists an invariant intrinsic metric. By Theorem 6.1, with this metric  is isometric to the circle defined in the plane
is isometric to the circle defined in the plane 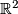 by an equation
by an equation 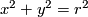 . Any isometry of this circle belongs to
. Any isometry of this circle belongs to 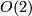 .
.
If all the homeomorphisms in the action preserve orientation, then by Theorem 9.10 the action is free, and the result follows from Theorem 9.3.
Assume that the action contains an orientation reversing homeomorphism. Then the group acts on the set of orientations. The orientation preserving homeomorphisms form a subgroup of index two. This is a cyclic group as above. Its complement consists of orientation reversing involutions. If the subgroup of orientation preserving homeomorphisms is trivial, then the whole group is of order 2 and the only non-trivial element is an orientation reversing involution, as in Theorem 9.9 above.
By Theorem 9.1, the action is equivalent to an action consisting of isometries of the circle. Its orientation preserving part
consists of rotations and is cyclic, say of order  . Its elements are rotations by angles
. Its elements are rotations by angles 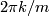 . The orientation reversing elements are reflections in diameters. There are
. The orientation reversing elements are reflections in diameters. There are  diameters.
diameters.
When 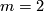 , that is the group contains only two orientation preserving homeomorphisms, the whole group is the cartesian product of two cyclic groups of order 2. It is called Klein's Vierergruppe or dihedral group
, that is the group contains only two orientation preserving homeomorphisms, the whole group is the cartesian product of two cyclic groups of order 2. It is called Klein's Vierergruppe or dihedral group 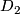 . It contains two reflections in diameters orthogonal to each other, the symmetry in the center of the circle and the identity.
. It contains two reflections in diameters orthogonal to each other, the symmetry in the center of the circle and the identity.
If the number of orientation preserving homeomorphisms is 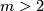 , then the whole group is called the dihedral group
, then the whole group is called the dihedral group 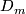 . It is
the symmetry group of an
. It is
the symmetry group of an  -sided regular polygon.
-sided regular polygon.

10 Exotic relatives of 1-manifolds
As we eliminate the Hausdorff or second countability property, the theory becomes somehow weird, but many aspects survive.
10.1 First examples of non-Hausdorff 1-manifolds
1. Line with two origins.
In the disjoint union of two copies  identify each point of one of the copies different from the origin with its corresponding point from the second copy:
identify each point of one of the copies different from the origin with its corresponding point from the second copy:
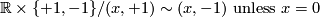 .
This space has a single point for each nonzero real number
.
This space has a single point for each nonzero real number  and two points
and two points 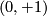 and
and 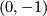 taking place of the origin. Each neighborhood of
taking place of the origin. Each neighborhood of 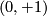 intersects each neighborhood of
intersects each neighborhood of 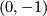 , so the space is not Hausdorff.
, so the space is not Hausdorff.
2. Branching line.
This is also a quotient space of two copies of the real line: 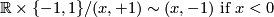 .
This space has a single point for each real number
.
This space has a single point for each real number 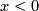 and two points
and two points 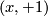 ,
, 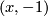 for every non-negative
for every non-negative  . As in the line with two origins above, in this space there is only one pair of points that have no disjoint neighborhoods:
. As in the line with two origins above, in this space there is only one pair of points that have no disjoint neighborhoods: 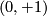 and
and 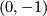 .
.
10.2 Spaces of leaves
At first glance, the examples above of non-Hausdorff 1-manifolds look artificial. However they appear naturally in some classical mathematical contexts. For example, the branching line is homeomorphic to the space of leaves of the following foliation of the plane 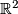 . The leaves are the vertical lines
. The leaves are the vertical lines
 with
with 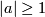 and the graphs
and the graphs 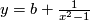 with
with 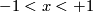 and arbitrary real
and arbitrary real  . In other words, the branching line is homeomorphic to the quotient space of
. In other words, the branching line is homeomorphic to the quotient space of 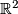 by partition into these lines and graphs. The leaves
by partition into these lines and graphs. The leaves 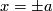 correspond to points
correspond to points 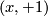 ,
, 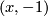 for non-negative
for non-negative  , the leaves
, the leaves 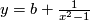 with
with 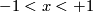 correspond to points
correspond to points 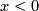 .
.
Similarly, the line with two origins can be identified with the space of leaves of a foliation of the cylinder 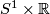 .
.
Although at first glance the space of leaves of a foliation looks substantially more natural than descriptions of non-Hausdorff 1-manifolds as quotient spaces of some 1-manifolds, they are not far away from each other: in either case we deal with factorization of a nice Hausdorff space, but factorization easily gives rise to a non-Hausdorff space.
10.3 Uncountable family of non-homeomorphic connected non-Hausdorff 1-manifolds
If we enlarge the collection of spaces by eliminating the Hausdorff property, then the number of topological types of connected spaces becomes uncountable.
Indeed, one can take the disjoint union of two copies of the line  and identify
an open set in one of them with its copy in the other one by the identity map. The quotient space is connected and satisfies all the
requirements from the definition of 1-manifold except the Hausdorff axiom. In this way one can construct uncountably many pairwise non-homeomorphic spaces. To prove that they are not homeomorphic, one can use, for example, the topological type of the subset formed by those points that do not separate the space.
and identify
an open set in one of them with its copy in the other one by the identity map. The quotient space is connected and satisfies all the
requirements from the definition of 1-manifold except the Hausdorff axiom. In this way one can construct uncountably many pairwise non-homeomorphic spaces. To prove that they are not homeomorphic, one can use, for example, the topological type of the subset formed by those points that do not separate the space.
10.4 Non-orientable non-Hausdorff 1-manifolds
The definition of orientation generalizes straightforwardly to non-Hausdorff 1-manifolds. Unlike usual 1-manifolds, there exist non-Hausdorff 1-manifolds that are non-orientable.
For example, the quotient space of the open interval 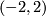 under identification
under identification 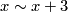 for
for 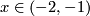 is a non-Hausdorff 1-manifold which does not admit any orientation.
is a non-Hausdorff 1-manifold which does not admit any orientation.
10.5 Differential structures
The notion of differential structure has a natural generalization to non-Hausdorff 1-manifolds. Let  be a non-Hausdorff 1-manifold, that is a second countable topological space such that each point of
be a non-Hausdorff 1-manifold, that is a second countable topological space such that each point of  has a neighborhood homeomorphic either to
has a neighborhood homeomorphic either to  or
or  . Let
. Let  be either a natural number, or
be either a natural number, or  . A sheaf
. A sheaf 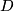 of real valued functions on
of real valued functions on  is called a differential structure of class
is called a differential structure of class  or just
or just  -structure if it satisfies the following condition: for any open set
-structure if it satisfies the following condition: for any open set 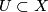 , a section
, a section 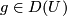 and a function
and a function 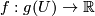 of class
of class  (i.e., a function having the first
(i.e., a function having the first  continuous derivatives
continuous derivatives  ,
, 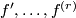 if
if  is finite and derivatives of all natural orders if
is finite and derivatives of all natural orders if 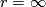 ), the composition
), the composition 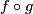 belongs to
belongs to 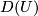 .
.
If each point 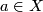 has a neighborhood
has a neighborhood 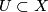 homeomorphic to
homeomorphic to  or
or  such that a
such that a  -structure
-structure 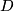 , as a sheaf, induces on
, as a sheaf, induces on  a sheaf isomorphic to the sheaf on
a sheaf isomorphic to the sheaf on  or
or  of functions of class
of functions of class  , then the
, then the  -structure
-structure 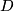 is called non-singular. A 1-manifold equipped with a non-singular
is called non-singular. A 1-manifold equipped with a non-singular  -structures is a
-structures is a  -manifold of dimension 1.
-manifold of dimension 1.
Any 1-manifold admits a non-singular  -structure, and any two homeomorphic
-structure, and any two homeomorphic  -manifolds of dimension 1 are diffeomorphic, see Section 6.3 above.
-manifolds of dimension 1 are diffeomorphic, see Section 6.3 above.
10.6 Homeomorphic, but non-diffeomorphic non-Hausdorff 1-manifolds
There exist two homeomorphic, but not diffeomorphic non-Hausdorff 1-manifolds. In order to construct such an example,
take a pair of monotone decreasing sequences 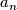 and
and 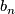 on
on  convergent to 0. There exists a homeomorphism
convergent to 0. There exists a homeomorphism 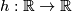 with
with 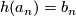 for all
for all  , but one can find sequences for which there is no diffeomorphism with this property. For example, this is the case for
, but one can find sequences for which there is no diffeomorphism with this property. For example, this is the case for 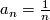 and
and 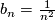 . Take such a pair of sequences. Let
. Take such a pair of sequences. Let 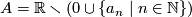 and
and 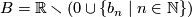 . By the identity map of
. By the identity map of  attach one copy of
attach one copy of  to another and denote the result by
to another and denote the result by  . Similarly, in the disjoint sum of two copies of
. Similarly, in the disjoint sum of two copies of  identify by the identity map the copies of
identify by the identity map the copies of  and denote the result by
and denote the result by  . The homeomorphism
. The homeomorphism  defines a homeomorphism
defines a homeomorphism 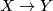 , on the other hand there is no diffeomorphism between
, on the other hand there is no diffeomorphism between  and
and  , because if one existed, it would map
, because if one existed, it would map  to
to  (as the sets of separating points) and extend to a diffeomorphism of
(as the sets of separating points) and extend to a diffeomorphism of  mapping
mapping 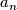 to
to 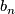 .
.
10.7 Relatives of 1-manifolds without countable base
One can easily construct a topological space which satisfies all the conditions of the definition of a 1-manifold except second countability by taking the disjoint sum of an uncountable number of copies of  (or any other 1-manifold). There are more interesting examples, which are connected. Most famous of them is the long line.
(or any other 1-manifold). There are more interesting examples, which are connected. Most famous of them is the long line.
10.8 Sheaf of germs of functions on a 1-manifold
The sheaf of germs of continuous functions on a 1-manifold is locally homeomorphic to  or
or  . So, it satisfies one condition (out of three) of the definition of a 1-manifold. The sheaf of germs of differentiable functions on a 1-manifold has a natural differential structure.
. So, it satisfies one condition (out of three) of the definition of a 1-manifold. The sheaf of germs of differentiable functions on a 1-manifold has a natural differential structure.
11 References
- [Fuks&Rokhlin1984] D. B. Fuks and V. A. Rokhlin, Beginner's course in topology. Geometric chapters. Translated from the Russian by A. Iacob. Universitext. Springer Series in Soviet Mathematics. Springer-Verlag, Berlin, 1984. MR759162 (86a:57001) Zbl 0562.54003
- [Gale1987] D. Gale, The Teaching of Mathematics: The Classification of 1-Manifolds: A Take-Home Exam, Amer. Math. Monthly 94 (1987), no.2, 170–175. MR1541035 Zbl 0621.57001
- [Ghys2001] E. Ghys, Groups acting on the circle, Enseign. Math. (2) 47 (2001), no.3-4, 329–407. MR1876932 (2003a:37032) Zbl 1044.37033
- [Moore1920] R. L. Moore, Concerning simple continuous curves, Trans. Amer. Math. Soc. 21 (1920), no.3, 333–347. MR1501148 () Zbl 47.0519.08
- [Ward1936] A. J. Ward, The topological characterization of an open linear interval, Proc. London Math. Soc.(2) 41 (1936), 191-198. MR1577110 Zbl 62.0693.02
12 External links
- The Encylopedia of Mathematics article on one-dimensional manifolds.
- The Encylopedia of Mathematics article on lines.
- The Wikipedia page about curves.