4-manifolds: 1-connected
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
[edit] 1 Introduction
Any finitely presentable group may occur as the fundamental group of a smooth closed 4-manifold. On the other hand, the class of simply connected (topological or smooth) 4-manifolds still appears to be quite rich, so it appears reasonable to consider the classification of simply connected 4-manifolds in particular.
It appears that the intersection form is the main algebro-topological invariant of simply-connected 4-manifolds.
[edit] 2 Construction and examples, their intersection forms
...
[edit] 2.1 First examples
The first examples that come to one's mind are the 4-sphere  , the complex projective space
, the complex projective space 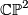 , the complex projective space with its opposite (non-complex) orientation
, the complex projective space with its opposite (non-complex) orientation 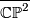 , the product
, the product 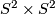 , various connected sums of these, and in particular
, various connected sums of these, and in particular 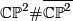 .
.
The intersection form of the 4-sphere is the "empty form" of rank 0. The intersection forms of the others are given by
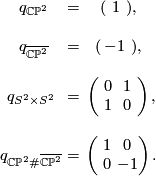
The manifolds 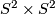 and
and 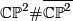 both have indefinite intersection forms of same rank and signature, but of different type. Therefore they are not homotopy-equvialent.
both have indefinite intersection forms of same rank and signature, but of different type. Therefore they are not homotopy-equvialent.
[edit] 2.2 Hypersurfaces in CP3
For an integer 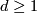 we define a subset
we define a subset 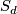 of
of 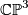 by the formula
by the formula
![\displaystyle S_d = \{ X_0^d + X_1^d + X_2^d + X_3^d = 0 | [X_0:X_1:X_2:X_3] \in \mathbb{CP}^3 \} .](/images/math/2/9/e/29e4e39ed8f3b8a56332f16a391355a5.png)
It is easy to check that in each chart of 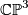 the
the 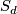 is cut out transversally by the homogeneous polynomial of degree
is cut out transversally by the homogeneous polynomial of degree  . Therefore,
. Therefore, 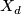 is a submanifold, in fact, an algebraic hypersurface. This is a special case of a complete intersection.
is a submanifold, in fact, an algebraic hypersurface. This is a special case of a complete intersection.
By the Lefschetz hyperplane section theorem the hypersurface 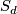 is simply connected. Its intersection form may be computed as follows: First one computes the Chern classes of
is simply connected. Its intersection form may be computed as follows: First one computes the Chern classes of 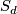 . Evaluating the second Chern class on the fundamental class
. Evaluating the second Chern class on the fundamental class ![[S_d]](/images/math/a/4/9/a49b4dba1c1ac9187e43c9bdf97a3b36.png) yields the Euler characteristic and therefore the rank of
yields the Euler characteristic and therefore the rank of 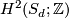 . Likewise, by computing the Pontryagin class and using the Hirzebruch signature theorem, stating that for a closed oriented 4-manifold
. Likewise, by computing the Pontryagin class and using the Hirzebruch signature theorem, stating that for a closed oriented 4-manifold  one has
one has
![\displaystyle \text{sign}(X) = \frac{1}{3} \langle p_1(TX), [X] \rangle \ ,](/images/math/a/1/b/a1b0529dad931caf34c26ada5e9fb3aa.png)
one computes the signature of 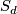 . Whether the intersection form is even or odd may be seen from the second Stiefel-Whitney class
. Whether the intersection form is even or odd may be seen from the second Stiefel-Whitney class 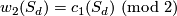 .
.
There are three facts that we need to use:
- The normal bundle
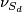 of
of 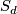 in
in 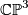 is given by
is given by 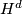 , where
, where  is the line bundle dual to the hyperplane
is the line bundle dual to the hyperplane 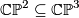 . Its first Chern class
. Its first Chern class  generates the cohomology ring of
generates the cohomology ring of 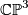 .
.
- The hypersurface
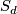 is Poincaré dual to the class
is Poincaré dual to the class 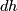 , or equivalently
, or equivalently ![\langle h^2,[S_d] \rangle = d](/images/math/9/a/5/9a5e59cb08121b975bc42647d339629e.png) .
.
- The total Chern class of
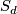 is given by
is given by
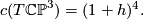
We can now apply the Whitney sum formula for the total Chern class to the splitting 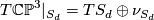 ,
,
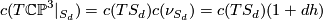
which we can invert to obtain the formula
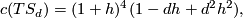
and in particular
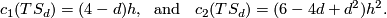
We compute the Euler characteristic ![\chi(S_d) = \langle c_2(S_d), [S_d] \rangle = (6-4d+d^2)d](/images/math/6/3/5/63598017801eb57b3a64b14c43099927.png) by the above mentioned fact. The first Pontryagin class
by the above mentioned fact. The first Pontryagin class 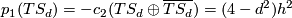 yields the signature
yields the signature 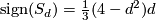 . We summarise
. We summarise
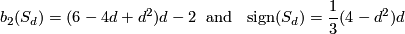
Furthermore 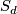 is spin if and only if
is spin if and only if  is even. This is because we have
is even. This is because we have
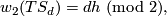
and because the inclusion 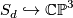 yields an injective restriction map in second cohomology with
yields an injective restriction map in second cohomology with 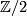 coefficients because of the hypersection theorem.
coefficients because of the hypersection theorem.
Summarising the above discussion, we have
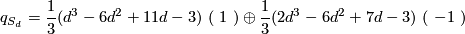
for  odd, and
odd, and
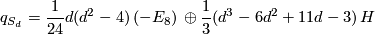
A particularly interesting special case is that of 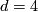 . The surface
. The surface 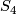 is a K3 surface. It is spin, has signature
is a K3 surface. It is spin, has signature 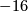 , and has
, and has 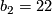 . By the classification results of indefinite intersection forms we know that the intersection form of
. By the classification results of indefinite intersection forms we know that the intersection form of 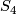 is given by
is given by
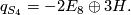
Blowing up the surface 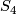 yields the manifold
yields the manifold 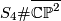 which now has an odd intersection form given by
which now has an odd intersection form given by
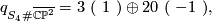
the same form as that of the 4-manifold 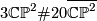 . Below we shall see that these two 4-manifolds are homeomorphic by Freedman's classification results, but not diffeomorphic because they have different Seiberg-Witten invariants.
. Below we shall see that these two 4-manifolds are homeomorphic by Freedman's classification results, but not diffeomorphic because they have different Seiberg-Witten invariants.
[edit] 2.3 Elliptic surfaces
[edit] 2.4 Branched coverings
[edit] 2.5 The E8 manifold
[edit] 3 Invariants
...
[edit] 4 Topological classification
By early work of Milnor and Whitehead the following theorem was known since 1958, and is based on a generalised Pontryagin-Thom construction:
For the classification of topological 4-manifolds Freedman achieved to use surgery theory in order to establish his famous
Theorem 4.2 (Freedman).
- Two simply-connected closed topological 4-manifolds are homeomorphic if and only if they have isomorphic intersection forms and the same Kirby-Siebenmann invariant.
- Given any even unimodular symmetric bilinear form
 over
over  there is, up to homeomorphism, a unique simply connected topological 4-manifold with intersection form
there is, up to homeomorphism, a unique simply connected topological 4-manifold with intersection form  .
.
- Given any odd unimodular symmetric bilinear form
 over
over  there are, up to homeomorphism, precisely two simply connected topological 4-manifolds with intersection form
there are, up to homeomorphism, precisely two simply connected topological 4-manifolds with intersection form  . One of them has non-trivial Kirby-Siebenmann invariant and therefore cannot be given a smooth structure.
. One of them has non-trivial Kirby-Siebenmann invariant and therefore cannot be given a smooth structure.
[edit] 5 Non-existence results for smooth 4-manifolds
Theorem 5.1 (Rohlin). A smooth closed 4-manifold that is spin, and therefore has even intersection form, has its signature divisible by 16.
By Freedman's theorem we know that there are closed simply connected topological 4-manifolds  with even intersection form and
with even intersection form and 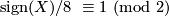 , as for instance the
, as for instance the 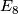 manifold
manifold 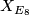 . By Rohlin's theorem these manifolds cannot admit a smooth structure. However, the manifold
. By Rohlin's theorem these manifolds cannot admit a smooth structure. However, the manifold 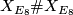 might so because its signature is equal to 16.
might so because its signature is equal to 16.
Using methods from gauge theory Donaldson was able to prove his famous theorem on the intersection form of smooth definite 4-manifolds:
Theorem 5.2 (Donaldson). Let  be a smooth closed 4-manifold with definite intersection form
be a smooth closed 4-manifold with definite intersection form 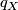 . Then
. Then 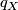 is diagonal, i.e. it is the direct sum of the 1-dimensional forms
is diagonal, i.e. it is the direct sum of the 1-dimensional forms 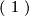 in the positive definite case, and of the forms
in the positive definite case, and of the forms 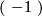 in the negative definite case.
in the negative definite case.
By Donaldson's theorem, the topological 4-manifold 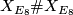 does not admit a smooth structure either, neither does any of the manifolds
does not admit a smooth structure either, neither does any of the manifolds 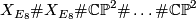 with odd intersection form. In fact, it is an algebraic theorem due to Eichler [Milnor&Husemoller1973] that there is a unique decomposition theorem for definite forms, and so no two of the forms
with odd intersection form. In fact, it is an algebraic theorem due to Eichler [Milnor&Husemoller1973] that there is a unique decomposition theorem for definite forms, and so no two of the forms 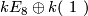 with different values of
with different values of 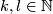 are isomorphic.
are isomorphic.
[edit] 6 The Seiberg-Witten invariants
...
[edit] 7 Failure of the h-cobordism theorem
...
[edit] 8 Further discussion
...
[edit] 9 References
- [Milnor&Husemoller1973] J. Milnor and D. Husemoller, Symmetric bilinear forms, Springer-Verlag, New York, 1973. MR0506372 (58 #22129) Zbl 0292.10016