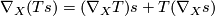Tensor derivative
(Difference between revisions)
m (→Definition) |
|||
| Line 1: | Line 1: | ||
{{Authors|Jost Eschenburg}}{{Stub}} | {{Authors|Jost Eschenburg}}{{Stub}} | ||
| − | == Definition == | + | ==Definition == |
<wikitex>; | <wikitex>; | ||
Let $M$ be a smooth manifold and $E,E'$ vector bundles over $M$, both equipped with a [[Covariant derivative|covariant derivative]] $\nabla$. | Let $M$ be a smooth manifold and $E,E'$ vector bundles over $M$, both equipped with a [[Covariant derivative|covariant derivative]] $\nabla$. | ||
Revision as of 13:16, 15 March 2013
|
The user responsible for this page is Jost Eschenburg. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Definition
Let  be a smooth manifold and
be a smooth manifold and 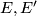 vector bundles over
vector bundles over  , both equipped with a covariant derivative
, both equipped with a covariant derivative  .
Then the vector bundle
.
Then the vector bundle 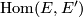 of bundle homomorphisms (sometimes called tensors) inherits another covariant derivative
of bundle homomorphisms (sometimes called tensors) inherits another covariant derivative
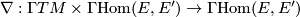 called the tensor derivative which is defined as follows:
called the tensor derivative which is defined as follows:
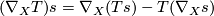 (1)
(1)for any 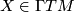 and
and 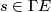 .
The definition is made such that the application of
tensors (sections in
.
The definition is made such that the application of
tensors (sections in 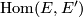 ) to sections in
) to sections in  satisfies the Leibniz product rule:
satisfies the Leibniz product rule:
The corresponding curvature tensors of the bundles  ,
, 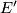 and
and 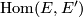 are related similarly:
are related similarly:
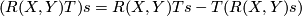 (2)
(2)for any 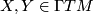 and
and 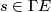 .
.