Tensor derivative
|
The user responsible for this page is Jost Eschenburg. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Definition
Let  be a smooth manifold and
be a smooth manifold and 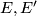 vector bundles over
vector bundles over  , both equipped with a covariant derivative
, both equipped with a covariant derivative 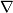 .
Then the vector bundle
.
Then the vector bundle 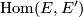 of bundle homomorphisms (sometimes called tensors) inherits another covariant derivative
of bundle homomorphisms (sometimes called tensors) inherits another covariant derivative
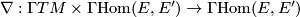 called the tensor derivative which is defined as follows:
called the tensor derivative which is defined as follows:
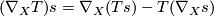
for any 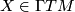 and
and 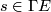 .
The definition is made such that the application of
tensors (sections in
.
The definition is made such that the application of
tensors (sections in 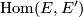 ) to sections in
) to sections in  satisfies the Leibniz product rule:
satisfies the Leibniz product rule:
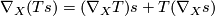
The corresponding curvature tensors of the bundles  ,
, 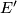 and
and 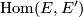 are related similarly:
are related similarly:
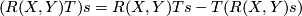
for any 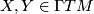 and
and 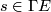 .
.
A tensor 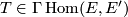 is called parallel if its tensor derivative vanishes,
is called parallel if its tensor derivative vanishes, 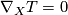 for all
for all 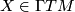 .
.
2 Examples
- A (semi-)Riemannian metric
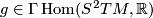 is parallel for its Levi-Civita connection.
is parallel for its Levi-Civita connection.
- A Riemannian manifold has parallel curvature tensor
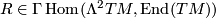 iff it is locally symmetric.
iff it is locally symmetric.
- A submanifold
 has parallel second fundamental form
has parallel second fundamental form 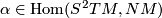 iff
iff  is locally extrinsic symmetric.
is locally extrinsic symmetric.
For further information see [Husemoller1994] and [Kobayashi&Nomizu1963].
3 References
- [Husemoller1994] D. Husemoller, Fibre bundles, 3rd ed., Springer-Verlag, 1994. MR1249482 (94k:55001) Zbl 0794.55001
- [Kobayashi&Nomizu1963] S. Kobayashi and K. Nomizu, Foundations of differential geometry. Vol I, Interscience Publishers, a division of John Wiley & Sons, New York-London, 1963. MR1393940 (97c:53001a) Zbl 0508.53002