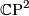Stable classification of 4-manifolds
|
The user responsible for this page is Matthias Kreck. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
In this page we report about the stable classification of closed oriented  -manifolds. We will begin with a special class of closed oriented
-manifolds. We will begin with a special class of closed oriented  -manifolds, namely those, where the universal covering is not spinnable.
-manifolds, namely those, where the universal covering is not spinnable.
2 Construction and examples I
We begin with the construction of two classes of manifolds which can be used to give many stable diffeomorphism types of non-spinnable  -manifolds. The first is:
-manifolds. The first is:
The second is a large class of manifolds associated to certain algebraic data.
Let  be a finitely presentable group. Then for each element
be a finitely presentable group. Then for each element  in
in 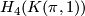 there is a smooth, closed, connected, oriented, non-spinnable manifold
there is a smooth, closed, connected, oriented, non-spinnable manifold 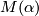 with signature zero, fundamental group
with signature zero, fundamental group  and
and ![u_*([M]) = \alpha](/images/math/a/2/1/a2132e46dc400eefcf637f8aa6b6ff65.png) . This is proved in several steps by first using the Atiyah-Hirzebruch spectral sequence) and the fact that the oriented bordism groups are zero in degree
. This is proved in several steps by first using the Atiyah-Hirzebruch spectral sequence) and the fact that the oriented bordism groups are zero in degree  ,
,  and
and  : see Oriented bordism to show that there is a closed, smooth, oriented manifold
: see Oriented bordism to show that there is a closed, smooth, oriented manifold  together with a map
together with a map 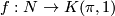 with
with ![f_*([M]) = \alpha](/images/math/8/a/a/8aa0b2b33192cb54dda92fbb8dd7c2b0.png) and signature zero. Then by surgeries on
and signature zero. Then by surgeries on  - and
- and  -dimensional spheres one changes
-dimensional spheres one changes  and
and  in such a way, that
in such a way, that  is connected and
is connected and 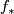 is an isomorphism on
is an isomorphism on 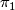 (reference). Finally we form the connected sum with
(reference). Finally we form the connected sum with 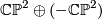 to make sure that
to make sure that  is non-spinnable. This manifold is of course not unique but we will see that it is unique up to stable diffeomorphisms and we abbreviate it by
is non-spinnable. This manifold is of course not unique but we will see that it is unique up to stable diffeomorphisms and we abbreviate it by
3 Invariants
The following is a complete list of invariants for the stable classification of closed, smooth oriented  -manifolds whose universal covering is not spinnable:
-manifolds whose universal covering is not spinnable:
- The Euler characteristic
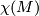
- The signature
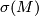
- The fundamanetal group
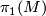
- The image of the fundamental class
![[u_*([M])]\in H_4(K(\pi_1(M),1)/Out(\pi_1(M))](/images/math/2/7/a/27a7f07e253ddaae67da2599a1a37142.png) of
of  .
.
Here 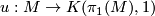 is a classifying map of the universal covering and
is a classifying map of the universal covering and 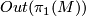 is the outer automorphism group which acts on the homology of
is the outer automorphism group which acts on the homology of 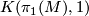 .
.
4 Classification
Theorem 4.1. Let  and
and  be
be  -dimensional compact smooth manifolds with non-spinnable universal covering. Then
-dimensional compact smooth manifolds with non-spinnable universal covering. Then  and
and  are stably diffeomorphic if and only if the invariants above agree.
are stably diffeomorphic if and only if the invariants above agree.
The proof of this result is an easy consequence of the general stable classification theorem ([Kreck1999], Stable classification of manifolds). Namely, the normal  -type is
-type is 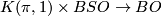 , see Stable classification of manfifolds. Thus the
, see Stable classification of manfifolds. Thus the  -bordism group is
-bordism group is 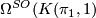 , which by the Atiyah-Hirzebruch spectral sequence is ismorphic to
, which by the Atiyah-Hirzebruch spectral sequence is ismorphic to 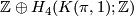 under the signature and the image of the fundamental class. Now the statement follows from Theorem 3.1 of Stable classification of manifolds.
under the signature and the image of the fundamental class. Now the statement follows from Theorem 3.1 of Stable classification of manifolds.
The different stable diffeomorphism classes of manifolds with fundamental group  are given by
are given by 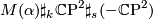 . Here $k+s + \chi
. Here $k+s + \chi
![\displaystyle \xymatrix{ B \ar[r]^{} \ar[d]^{} & K(\pi, 1) \ar[d]^{\hat w_2} \\ BSO \ar[r]^{w_2} & K(\Zz/2, 2) }](/images/math/d/3/b/d3ba1995973224eb01a13d2df92e832d.png)
5 Further discussion
...
6 References
- [Kreck1999] M. Kreck, Surgery and duality, Ann. of Math. (2) 149 (1999), no.3, 707–754. MR1709301 (2001a:57051) Zbl 0935.57039