Stable classification of manifolds
|
The user responsible for this page is Matthias Kreck. No other user may edit this page at present. |
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Introduction
Two closed smooth manifolds  and
and  of dimension
of dimension  are called stably diffeomorphic if there is an integer
are called stably diffeomorphic if there is an integer  such that
such that 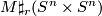 is diffeomorphic to
is diffeomorphic to 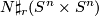 . By
. By 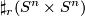 we mean the connected sum with
we mean the connected sum with  copies of
copies of  . Note that since
. Note that since  has an orientation reversing diffeomorphism the connect sum with it is well defined (see Lemma 2.1 of Connected sum). We present a method which reduces the stable classification to a bordism problem.
has an orientation reversing diffeomorphism the connect sum with it is well defined (see Lemma 2.1 of Connected sum). We present a method which reduces the stable classification to a bordism problem.
2 The normal k-type
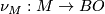 . We consider an
. We consider an  -factorization
-factorization 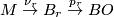
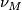 [Spanier1981], page 440. This means that
[Spanier1981], page 440. This means that 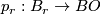 is a fibration, where
is a fibration, where  is a
is a  -complex, the map
-complex, the map 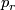 is
is  -connected, i.e. the homotopy groups of the fibre vanish in degree
-connected, i.e. the homotopy groups of the fibre vanish in degree 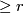 , and the map
, and the map 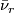 is an
is an  -equivalence.
-equivalence.
Definition 1.1. The fibre homotopy type of the fibration 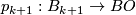 is an invariant of
is an invariant of  and is called the normal
and is called the normal  -type of
-type of  denoted
denoted 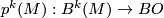 [Kreck1999].
[Kreck1999].
In particular, the normal  -type does not depend on the choice of an embedding.
-type does not depend on the choice of an embedding.
For example the normal  -type of an oriented manifold is the universal covering
-type of an oriented manifold is the universal covering
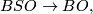
 -type of a non-orientable manifold is the identity map
-type of a non-orientable manifold is the identity map

 -type of a simply connected manifold
-type of a simply connected manifold  depending on whether the second Stiefel-Whitney class vanishes or not: If
depending on whether the second Stiefel-Whitney class vanishes or not: If 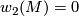 (M admits a
(M admits a  -structure) its normal
-structure) its normal  -type is the fibration
-type is the fibration
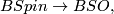
if 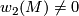 (
( does not admit a
does not admit a  -structure) then it's normal
-structure) then it's normal  -type is the fibration
-type is the fibration
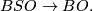
 -type of a Spin-manifold
-type of a Spin-manifold  is
is 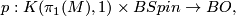
 is the composition of the projection to
is the composition of the projection to 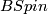 and the projection
and the projection 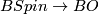 . The normal
. The normal  -type of a manifold
-type of a manifold  such that the universal covering
such that the universal covering 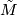 does not admit a
does not admit a  -structure, is
-structure, is 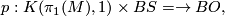
 is the composition of the projection to
is the composition of the projection to 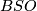 and the projection
and the projection 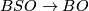 . The case where
. The case where 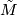 admits a
admits a  -structure but
-structure but  doesn't, is treated in Stable classification of simply connected 4-manifolds.
doesn't, is treated in Stable classification of simply connected 4-manifolds.
Definition 1.2. If 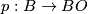 is the normal
is the normal  -type of a manifold
-type of a manifold  , the choice of a homotopy class of lifts
, the choice of a homotopy class of lifts 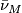 , which is a
, which is a  -equivalence is called a normal
-equivalence is called a normal  -smoothing. We say that two normal
-smoothing. We say that two normal  -smoothings
-smoothings 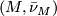 and
and 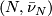 with same normal
with same normal  -type are diffeomorphic, if there is a diffeomorphism
-type are diffeomorphic, if there is a diffeomorphism 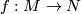 compatible with the normal
compatible with the normal  -smoothings. The latter means that if we have embedded
-smoothings. The latter means that if we have embedded  into
into 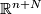 , we embed
, we embed  via the composition with
via the composition with  , so that
, so that 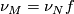 . Then we require that
. Then we require that 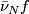 id fibre homotopic to
id fibre homotopic to 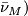 .
.
The group of homotopy classes of fibre homotopy self equivalences 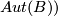 acts by composition on the normal
acts by composition on the normal  -smoothings and this action is free and transitive [Kreck1999]. Thus if one fixes a normal
-smoothings and this action is free and transitive [Kreck1999]. Thus if one fixes a normal  -smoothing the composition with elements of
-smoothing the composition with elements of 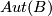 is a bijection from
is a bijection from 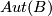 to the different normal
to the different normal  -smoothings.
-smoothings.
The stable classification of normal (k-1)-smoothings on 2k-dimensional manifolds
Above we defined stable diffeomorphisms. We can define stable diffeomorphisms of normal 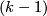 -smoothings of
-smoothings of 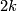 -dimensional manifolds
-dimensional manifolds 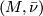 as follows. Suppose that we have two
as follows. Suppose that we have two 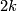 -dimensional Manifolds
-dimensional Manifolds  and
and  with same normal
with same normal 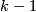 -type
-type 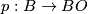 . We consider
. We consider 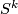 as the boundary of
as the boundary of 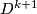 and equip it with the restriction of the the unique (up to homotopy) lift of the stable normal bundle to
and equip it with the restriction of the the unique (up to homotopy) lift of the stable normal bundle to  . Using this we obtain a lift of the stable normal bundle of
. Using this we obtain a lift of the stable normal bundle of 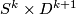 to
to  and consider its restriction to
and consider its restriction to 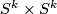 . If
. If 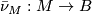 is a normal
is a normal 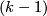 -smoothing of
-smoothing of  this together with the constructed lift of the stable normal bundle of
this together with the constructed lift of the stable normal bundle of 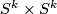 to
to  induces a well defined normal
induces a well defined normal 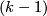 -smoothing of
-smoothing of 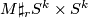 which we call
which we call 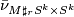 . We say that two normal
. We say that two normal 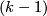 -smoothings in
-smoothings in  are stably diffeomorphic if the stabilized normal
are stably diffeomorphic if the stabilized normal 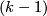 -smoothings are diffeomorphic.
-smoothings are diffeomorphic.
Theorem 3.1. [Kreck1999] Let  and
and  be
be 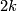 -dimensional closed smooth manifolds with same normal
-dimensional closed smooth manifolds with same normal 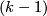 -type
-type  . Then two normal
. Then two normal 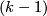 smoothings
smoothings 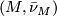 and
and 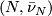 are stably diffeomorphic if and only if the bordism classes of
are stably diffeomorphic if and only if the bordism classes of 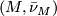 and
and 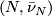 agree in the
agree in the  -bordism group
-bordism group 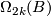 and the Euler characteristics agree:
and the Euler characteristics agree: 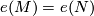 .
.
If  and
and  are compact manifolds with boundary and
are compact manifolds with boundary and 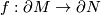 is a diffeomorphism compatible wirth the restriction of the normal
is a diffeomorphism compatible wirth the restriction of the normal 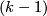 -smoothings to the boundaries, then
-smoothings to the boundaries, then  extends to a stable diffeomorphism of the normal
extends to a stable diffeomorphism of the normal 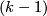 -smoothings if and only if
-smoothings if and only if 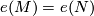 and the closed manifold obtained by gluing
and the closed manifold obtained by gluing  to
to 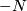 via
via  together with the normal structure given by
together with the normal structure given by 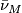 and
and 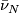 is zero bordant in
is zero bordant in 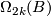 . Here by
. Here by 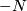 we mean
we mean  equipped with the normal
equipped with the normal 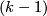 -smoothing which is given by the restriction to
-smoothing which is given by the restriction to 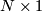 of the obvious normal structure on
of the obvious normal structure on ![N \times [0,1]](/images/math/1/0/a/10ab360ccfda496ad37e84475a637a83.png) extending the given structure on
extending the given structure on 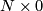 .
.
Thus two 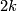 -dimensional closed manifolds
-dimensional closed manifolds  and
and  are stably diffeomorphic if and only if
are stably diffeomorphic if and only if 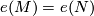 , they have the same normal
, they have the same normal 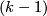 -type
-type 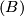 and admit bordant normal
and admit bordant normal 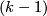 -smoothings in
-smoothings in  .
.
For simply connected closed smooth  -manifolds Wall [Wall1964] showed that they are stably diffeomorphic if and only both admit a
-manifolds Wall [Wall1964] showed that they are stably diffeomorphic if and only both admit a  -structure or both don't admit a
-structure or both don't admit a  -structure, the signatures and the Euler characteristics agree (he uses a different formulation in terms of the intersection forms but by the stable classification of unimodular quadratic forms this is equivalent to our conditions). This is a consequence of the Theorem 3.1. Namely under Wall's condition the normal
-structure, the signatures and the Euler characteristics agree (he uses a different formulation in terms of the intersection forms but by the stable classification of unimodular quadratic forms this is equivalent to our conditions). This is a consequence of the Theorem 3.1. Namely under Wall's condition the normal  -types agree and the
-types agree and the  -bordisms groups correspond to
-bordisms groups correspond to  bordism resp. oriented bordism groups which are detected by the signature. Thus we obtain
bordism resp. oriented bordism groups which are detected by the signature. Thus we obtain
Corollary 3.2. [Wall1964] Let  and
and  be simply connected closed smooth
be simply connected closed smooth  -manifolds, then
-manifolds, then  and
and  are stably diffeomorphic if and only if they are both spinnable or both not spinnable and the signature and Euler characteristics agree.
are stably diffeomorphic if and only if they are both spinnable or both not spinnable and the signature and Euler characteristics agree.
Wall proves his theorem in two steps, the first is an (unstable) classification of simply connected  -manifolds up top
-manifolds up top  -cobordism. The second is the proof of a stable
-cobordism. The second is the proof of a stable  -cobordism theorem in dimension
-cobordism theorem in dimension  . The first part is a very special application of a big theory: Surgery. The proof of Theorem 3.1 is a special case of a modified surgery theory [Kreck1999].
. The first part is a very special application of a big theory: Surgery. The proof of Theorem 3.1 is a special case of a modified surgery theory [Kreck1999].
There are versions of the concepts and results of this page for  -manifolds or topological manifolds. Everything is the same if one replaces the normal bundles by the
-manifolds or topological manifolds. Everything is the same if one replaces the normal bundles by the  or topological normal bundles and
or topological normal bundles and 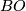 by the corresponding classifying spaces
by the corresponding classifying spaces 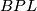 an
an 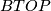 . Then one replaces the smooth
. Then one replaces the smooth  -bordism groups by the corresponding
-bordism groups by the corresponding  or topological
or topological  -bordism groups B-Bordism. Then Theorem 3.1. holds for
-bordism groups B-Bordism. Then Theorem 3.1. holds for  or topological manifolds where we classify up to stable
or topological manifolds where we classify up to stable  -homeomorphisms or stable homeomorphisms.
-homeomorphisms or stable homeomorphisms.
An unstable classification of some normal (k-1)-smoothings on 2k-dimensional manifolds
If 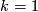 the normal
the normal  -type is the same if and only if the surfaces are both orientable or both non-orientable and one has a better Theorem, namely an unstable classification by the Euler characteristic (in this case the bordism class is determined by the Euler characteristic mod
-type is the same if and only if the surfaces are both orientable or both non-orientable and one has a better Theorem, namely an unstable classification by the Euler characteristic (in this case the bordism class is determined by the Euler characteristic mod  ). It is an interesting question, under which conditions one gets an unstable classification in higher dimensions. For manifolds with finite fundamental group one has the following result for
). It is an interesting question, under which conditions one gets an unstable classification in higher dimensions. For manifolds with finite fundamental group one has the following result for 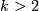 :
:
Theorem 6.1. [Kreck1999] Let  and
and  be
be 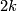 -dimensional compact smooth manifolds with same normal
-dimensional compact smooth manifolds with same normal 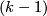 -type
-type  and
and 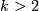 . Suppose that if the fundamental group is trivial and, if
. Suppose that if the fundamental group is trivial and, if  is even,
is even,  is of the form
is of the form 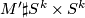 , or if the fundamental group is finite and
, or if the fundamental group is finite and  is of the form
is of the form 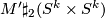 .
.
Then two normal 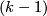 smoothings
smoothings 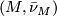 and
and 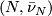 are diffeomorphic extending a diffeomorphism of the boundaries compatible with the normal
are diffeomorphic extending a diffeomorphism of the boundaries compatible with the normal 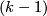 -smoothings, if and only if
-smoothings, if and only if 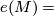 e(N) and the bordism classes of
e(N) and the bordism classes of 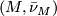 and
and 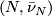 the closed manifold obtained by gluing
the closed manifold obtained by gluing  to
to 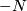 via
via  together with the normal structure given by
together with the normal structure given by 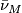 and
and 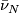 is zero bordant in
is zero bordant in 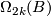 .
.
References
- [Kreck1999] M. Kreck, Surgery and duality, Ann. of Math. (2) 149 (1999), no.3, 707–754. MR1709301 (2001a:57051) Zbl 0935.57039
- [Spanier1981] E. H. Spanier, Algebraic topology, Springer-Verlag, 1981. MR666554 (83i:55001) Zbl 0810.55001
- [Wall1964] C. T. C. Wall, Diffeomorphisms of
 -manifolds, J. London Math. Soc. 39 (1964), 131–140. MR0163323 (29 #626) Zbl 0121.18101
-manifolds, J. London Math. Soc. 39 (1964), 131–140. MR0163323 (29 #626) Zbl 0121.18101