Knots, i.e. embeddings of spheres
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
See general introduction on embeddings, notation and conventions in [Skopenkov2016c,  1,
1,  3].
3].
2 Examples
Analogously to the Haefliger trefoil knot for 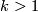 one constructs a smooth embedding
one constructs a smooth embedding 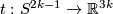 .
For
.
For  even this embedding is a generator of
even this embedding is a generator of 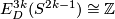 ; it is not smoothly isotopic to the standard embedding, but is piecewise smoothly isotopic to it [Haefliger1962].
It would be interesting to know if for
; it is not smoothly isotopic to the standard embedding, but is piecewise smoothly isotopic to it [Haefliger1962].
It would be interesting to know if for  odd this embedding is a generator of
odd this embedding is a generator of 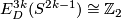 .
The last phrase of [Haefliger1962t] suggests that this is true for
.
The last phrase of [Haefliger1962t] suggests that this is true for 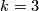 .
.
3 Readily calculable classification
For  the group
the group  has been described in terms of exact sequences involving the homotopy groups of spheres and the homotopy groups of the pairs
has been described in terms of exact sequences involving the homotopy groups of spheres and the homotopy groups of the pairs 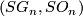 for
for 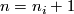 and
and 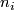 [Haefliger1966a], cf. [Levine1965], [Milgram1972], [Habegger1986].
Here
[Haefliger1966a], cf. [Levine1965], [Milgram1972], [Habegger1986].
Here 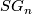 is the space of maps
is the space of maps 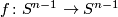 of degree
of degree  .
Restricting an element of
.
Restricting an element of 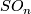 to
to 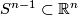 identifies
identifies 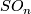 as a subspace of
as a subspace of 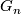 .
.
Some readily calculable corollaries of this classification are recalled in [Skopenkov2006,  3.3].
3.3].
4 Codimension 2 knots
For the best known specific case, i.e. for codimension 2 embeddings of spheres (in particular, for the classical theory of knots in 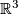 ), a complete readily calculable classification (in the sense of
Remark 1.1 of [Skopenkov2016c]) is neither known nor expected at the time of writing.
However, there is a vast literature on codimension 2 knots, most of which does not present a readily calculable classification.
See e.g. interesting papers [Farber1981], [Farber1983], [Kearton1983], [Farber1984].
), a complete readily calculable classification (in the sense of
Remark 1.1 of [Skopenkov2016c]) is neither known nor expected at the time of writing.
However, there is a vast literature on codimension 2 knots, most of which does not present a readily calculable classification.
See e.g. interesting papers [Farber1981], [Farber1983], [Kearton1983], [Farber1984].
On the other hand, if one studies embeddings up to the weaker relation of concordance, then much is known. See e.g. [Levine1969a] and [Ranicki1998].
5 References
- [Farber1981] M. Sh. Farber, Classification of stable fibered knots, Mat. Sb. (N.S.), 115(157):2(6) (1981) 223–262.
- [Farber1983] M. Sh. Farber, The classification of simple knots, Russian Math. Surveys, 38:5 (1983).
- [Farber1984] M. Sh. Farber, An algebraic classification of some even-dimensional spherical knots I, II, Trans. Amer. Math. Soc. 281 (1984), 507-528; 529-570.
- [Habegger1986] N. Habegger, Knots and links in codimension greater than 2, Topology, 25:3 (1986) 253--260.
- [Haefliger1962] A. Haefliger, Knotted
 -spheres in
-spheres in 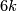 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Kearton1983] C. Kearton, An algebraic classification of certain simple even-dimensional knots, Trans. Amer. Math. Soc. 176 (1983), 1–53.
- [Levine1965] J. Levine, A classification of differentiable knots, Ann. of Math. (2) 82 (1965), 15–50. MR0180981 (31 #5211) Zbl 0136.21102
- [Levine1969a] J. Levine, Knot cobordism groups in codimension two, Comment. Math. Helv. 44 (1969), 229–244. MR0246314 (39 #7618) Zbl 0176.22101
- [Milgram1972] R. J. Milgram, On the Haefliger knot groups, Bull. of the Amer. Math. Soc., 78:5 (1972) 861--865.
- [Ranicki1998] A. Ranicki, High-dimensional knot theory, Springer-Verlag, 1998. MR1713074 (2000i:57044) Zbl 1059.19003
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
 3].
3].
2 Examples
Analogously to the Haefliger trefoil knot for 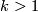 one constructs a smooth embedding
one constructs a smooth embedding 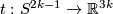 .
For
.
For  even this embedding is a generator of
even this embedding is a generator of 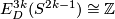 ; it is not smoothly isotopic to the standard embedding, but is piecewise smoothly isotopic to it [Haefliger1962].
It would be interesting to know if for
; it is not smoothly isotopic to the standard embedding, but is piecewise smoothly isotopic to it [Haefliger1962].
It would be interesting to know if for  odd this embedding is a generator of
odd this embedding is a generator of 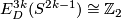 .
The last phrase of [Haefliger1962t] suggests that this is true for
.
The last phrase of [Haefliger1962t] suggests that this is true for 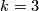 .
.
3 Readily calculable classification
For  the group
the group  has been described in terms of exact sequences involving the homotopy groups of spheres and the homotopy groups of the pairs
has been described in terms of exact sequences involving the homotopy groups of spheres and the homotopy groups of the pairs 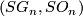 for
for 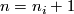 and
and 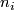 [Haefliger1966a], cf. [Levine1965], [Milgram1972], [Habegger1986].
Here
[Haefliger1966a], cf. [Levine1965], [Milgram1972], [Habegger1986].
Here 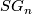 is the space of maps
is the space of maps 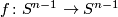 of degree
of degree  .
Restricting an element of
.
Restricting an element of 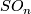 to
to 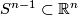 identifies
identifies 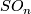 as a subspace of
as a subspace of 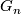 .
.
Some readily calculable corollaries of this classification are recalled in [Skopenkov2006,  3.3].
3.3].
4 Codimension 2 knots
For the best known specific case, i.e. for codimension 2 embeddings of spheres (in particular, for the classical theory of knots in 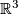 ), a complete readily calculable classification (in the sense of
Remark 1.1 of [Skopenkov2016c]) is neither known nor expected at the time of writing.
However, there is a vast literature on codimension 2 knots, most of which does not present a readily calculable classification.
See e.g. interesting papers [Farber1981], [Farber1983], [Kearton1983], [Farber1984].
), a complete readily calculable classification (in the sense of
Remark 1.1 of [Skopenkov2016c]) is neither known nor expected at the time of writing.
However, there is a vast literature on codimension 2 knots, most of which does not present a readily calculable classification.
See e.g. interesting papers [Farber1981], [Farber1983], [Kearton1983], [Farber1984].
On the other hand, if one studies embeddings up to the weaker relation of concordance, then much is known. See e.g. [Levine1969a] and [Ranicki1998].
5 References
- [Farber1981] M. Sh. Farber, Classification of stable fibered knots, Mat. Sb. (N.S.), 115(157):2(6) (1981) 223–262.
- [Farber1983] M. Sh. Farber, The classification of simple knots, Russian Math. Surveys, 38:5 (1983).
- [Farber1984] M. Sh. Farber, An algebraic classification of some even-dimensional spherical knots I, II, Trans. Amer. Math. Soc. 281 (1984), 507-528; 529-570.
- [Habegger1986] N. Habegger, Knots and links in codimension greater than 2, Topology, 25:3 (1986) 253--260.
- [Haefliger1962] A. Haefliger, Knotted
 -spheres in
-spheres in 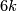 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Kearton1983] C. Kearton, An algebraic classification of certain simple even-dimensional knots, Trans. Amer. Math. Soc. 176 (1983), 1–53.
- [Levine1965] J. Levine, A classification of differentiable knots, Ann. of Math. (2) 82 (1965), 15–50. MR0180981 (31 #5211) Zbl 0136.21102
- [Levine1969a] J. Levine, Knot cobordism groups in codimension two, Comment. Math. Helv. 44 (1969), 229–244. MR0246314 (39 #7618) Zbl 0176.22101
- [Milgram1972] R. J. Milgram, On the Haefliger knot groups, Bull. of the Amer. Math. Soc., 78:5 (1972) 861--865.
- [Ranicki1998] A. Ranicki, High-dimensional knot theory, Springer-Verlag, 1998. MR1713074 (2000i:57044) Zbl 1059.19003
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
 3].
3].
2 Examples
Analogously to the Haefliger trefoil knot for 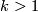 one constructs a smooth embedding
one constructs a smooth embedding 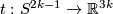 .
For
.
For  even this embedding is a generator of
even this embedding is a generator of 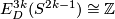 ; it is not smoothly isotopic to the standard embedding, but is piecewise smoothly isotopic to it [Haefliger1962].
It would be interesting to know if for
; it is not smoothly isotopic to the standard embedding, but is piecewise smoothly isotopic to it [Haefliger1962].
It would be interesting to know if for  odd this embedding is a generator of
odd this embedding is a generator of 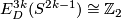 .
The last phrase of [Haefliger1962t] suggests that this is true for
.
The last phrase of [Haefliger1962t] suggests that this is true for 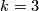 .
.
3 Readily calculable classification
For  the group
the group  has been described in terms of exact sequences involving the homotopy groups of spheres and the homotopy groups of the pairs
has been described in terms of exact sequences involving the homotopy groups of spheres and the homotopy groups of the pairs 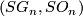 for
for 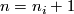 and
and 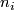 [Haefliger1966a], cf. [Levine1965], [Milgram1972], [Habegger1986].
Here
[Haefliger1966a], cf. [Levine1965], [Milgram1972], [Habegger1986].
Here 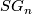 is the space of maps
is the space of maps 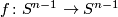 of degree
of degree  .
Restricting an element of
.
Restricting an element of 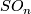 to
to 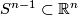 identifies
identifies 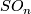 as a subspace of
as a subspace of 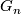 .
.
Some readily calculable corollaries of this classification are recalled in [Skopenkov2006,  3.3].
3.3].
4 Codimension 2 knots
For the best known specific case, i.e. for codimension 2 embeddings of spheres (in particular, for the classical theory of knots in 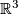 ), a complete readily calculable classification (in the sense of
Remark 1.1 of [Skopenkov2016c]) is neither known nor expected at the time of writing.
However, there is a vast literature on codimension 2 knots, most of which does not present a readily calculable classification.
See e.g. interesting papers [Farber1981], [Farber1983], [Kearton1983], [Farber1984].
), a complete readily calculable classification (in the sense of
Remark 1.1 of [Skopenkov2016c]) is neither known nor expected at the time of writing.
However, there is a vast literature on codimension 2 knots, most of which does not present a readily calculable classification.
See e.g. interesting papers [Farber1981], [Farber1983], [Kearton1983], [Farber1984].
On the other hand, if one studies embeddings up to the weaker relation of concordance, then much is known. See e.g. [Levine1969a] and [Ranicki1998].
5 References
- [Farber1981] M. Sh. Farber, Classification of stable fibered knots, Mat. Sb. (N.S.), 115(157):2(6) (1981) 223–262.
- [Farber1983] M. Sh. Farber, The classification of simple knots, Russian Math. Surveys, 38:5 (1983).
- [Farber1984] M. Sh. Farber, An algebraic classification of some even-dimensional spherical knots I, II, Trans. Amer. Math. Soc. 281 (1984), 507-528; 529-570.
- [Habegger1986] N. Habegger, Knots and links in codimension greater than 2, Topology, 25:3 (1986) 253--260.
- [Haefliger1962] A. Haefliger, Knotted
 -spheres in
-spheres in 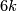 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Kearton1983] C. Kearton, An algebraic classification of certain simple even-dimensional knots, Trans. Amer. Math. Soc. 176 (1983), 1–53.
- [Levine1965] J. Levine, A classification of differentiable knots, Ann. of Math. (2) 82 (1965), 15–50. MR0180981 (31 #5211) Zbl 0136.21102
- [Levine1969a] J. Levine, Knot cobordism groups in codimension two, Comment. Math. Helv. 44 (1969), 229–244. MR0246314 (39 #7618) Zbl 0176.22101
- [Milgram1972] R. J. Milgram, On the Haefliger knot groups, Bull. of the Amer. Math. Soc., 78:5 (1972) 861--865.
- [Ranicki1998] A. Ranicki, High-dimensional knot theory, Springer-Verlag, 1998. MR1713074 (2000i:57044) Zbl 1059.19003
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.