Knots, i.e. embeddings of spheres
|
This page has not been refereed. The information given here might be incomplete or provisional. |
See general introduction on embeddings, notation and conventions in [Skopenkov2016c, $\S$1, $\S$2].
1 Examples
Analogously to the Haefliger trefoil knot for 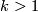 one constructs a smooth embedding
one constructs a smooth embedding 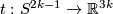 .
For
.
For  even this embedding is a generator of
even this embedding is a generator of 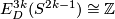 ; it is not smoothly isotopic to the standard embedding, but is piecewise smoothly isotopic to it [Haefliger1962].
It would be interesting to know if for
; it is not smoothly isotopic to the standard embedding, but is piecewise smoothly isotopic to it [Haefliger1962].
It would be interesting to know if for  odd this embedding is a generator of
odd this embedding is a generator of 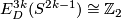 .
The last phrase of [Haefliger1962t] suggests that this is true for
.
The last phrase of [Haefliger1962t] suggests that this is true for 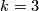 .
.
2 Classification
For some information see [Skopenkov2006, $\S$3.3].
(I would suggest including the classification of simple knots a la Kearton et. al. in this section.---John Klein)
3 References
- [Haefliger1962] A. Haefliger, Knotted
 -spheres in
-spheres in 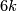 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
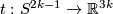 .
For
.
For  even this embedding is a generator of
even this embedding is a generator of 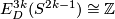 ; it is not smoothly isotopic to the standard embedding, but is piecewise smoothly isotopic to it [Haefliger1962].
It would be interesting to know if for
; it is not smoothly isotopic to the standard embedding, but is piecewise smoothly isotopic to it [Haefliger1962].
It would be interesting to know if for  odd this embedding is a generator of
odd this embedding is a generator of 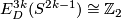 .
The last phrase of [Haefliger1962t] suggests that this is true for
.
The last phrase of [Haefliger1962t] suggests that this is true for 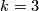 .
.
2 Classification
For some information see [Skopenkov2006, $\S$3.3].
(I would suggest including the classification of simple knots a la Kearton et. al. in this section.---John Klein)
3 References
- [Haefliger1962] A. Haefliger, Knotted
 -spheres in
-spheres in 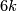 -space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
-space, Ann. of Math. (2) 75 (1962), 452–466. MR0145539 (26 #3070) Zbl 0105.17407
- [Haefliger1962t] A. Haefliger, Differentiable links, Topology, 1 (1962) 241--244
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.