Embeddings of manifolds with boundary: classification
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
Recall that some Unknotting Theorems hold for manifolds with boundary [Skopenkov2016c,  3], [Skopenkov2006,
3], [Skopenkov2006,  2]. In this page we present results peculiar for manifold with non-empty boundary.
2]. In this page we present results peculiar for manifold with non-empty boundary.
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3].
3].
If the category is omitted, then a result stated below holds in both the smooth and piecewise-linear (PL) category.
Theorem 1.1.
Every  -manifold
-manifold  with nonempty boundary PL-embeds into
with nonempty boundary PL-embeds into 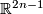 .
.
This result can be found in [Horvatic1971, theorem 5.2]
2 Unknotting Theorems
Theorem 2.1.
Assume  is a compact connected
is a compact connected  -manifold and either
-manifold and either
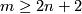 or
or
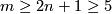 .
Then any two embeddings of
.
Then any two embeddings of  into
into  are isotopic.
are isotopic.
Condition 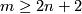 stands for General Position Theorem and condition
stands for General Position Theorem and condition 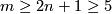 stands for Whitney-Wu Unknotting Theorem, see Unknotting Theorems, theorems 2.1 and 2.2 respectivly.
stands for Whitney-Wu Unknotting Theorem, see Unknotting Theorems, theorems 2.1 and 2.2 respectivly.
Theorem 2.2.
Assume  is a compact connected
is a compact connected  -manifold with non-empty boundary and one of the following conditions holds:
-manifold with non-empty boundary and one of the following conditions holds:
(a) 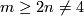
(b)  is
is  -connected,
-connected, 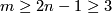
Then any two embeddings of  into
into  are isotopic.
are isotopic.
Part (a) of this theorem in case 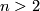 can be found in [Edwards1968,
can be found in [Edwards1968,  4, corollary 5]. Case
4, corollary 5]. Case  is clear. Case
is clear. Case  can be derived from deleted square criterion, \site{Skopenkov2006}.
can be derived from deleted square criterion, \site{Skopenkov2006}.
Theorem 2.3.
[The Haefliger-Zeeman unknotting theorem]
For every 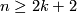 ,
, 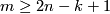 and closed
and closed  -connected
-connected  -manifold
-manifold  , any two embeddings of
, any two embeddings of  into
into  are isotopic.
are isotopic.
Theorem 2.4.
Assume  is a compact
is a compact  -manifold,
-manifold, 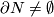 . If
. If  is
is  -connected,
-connected, 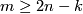 and
and 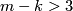 then any two embeddings of
then any two embeddings of  into
into  are isotopic.
are isotopic.
This result can be found in [Hudson1969, Theorem 10.3]
3 Construction and examples
...
4 Invariants
...
5 Classification
Theorem 5.1.[Becker-Glover]
Let  be a closed homologically
be a closed homologically  -connected
-connected  -manifold
and
-manifold
and 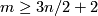 .
The cone map
.
The cone map 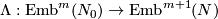 is one-to-one
for
is one-to-one
for
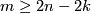 and is surjective
for
and is surjective
for 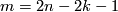 .
.
6 Further discussion
...
7 References
- [Becker&Glover1971] J. Becker and H. Glover, Note on the embedding of manifolds in Euclidean space, Proc. Am. Math. Soc. 27 (1971), 405-410. MR0268903 (42 #3800) Zbl 0207.22402
- [Edwards1968] Edwards, C. H. Unknotting polyhedral homology manifolds, Michigan Math. J. 15 (1968), 81-95. MR226629 Zbl 0167.52001
- [Horvatic1971] K. Horvatic, On embedding polyhedra and manifolds, Trans. Am. Math. Soc. 157 (1971), 417-436.
- [Hudson1969] J. F. P. Hudson, Piecewise linear topology, W. A. Benjamin, Inc., New York-Amsterdam, 1969. MR0248844 (40 #2094) Zbl 0189.54507
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.