Embeddings of manifolds with boundary: classification
m |
m |
||
| Line 23: | Line 23: | ||
<!--We state the results below in piecewise-linear (PL) category.--> | <!--We state the results below in piecewise-linear (PL) category.--> | ||
| − | We state only the results that can be deduced from the Haefliger-Weber deleted product criterion \cite[$\S$ 5]{Skopenkov2006}, see \cite[6.4]{Haefliger1963}, \cite[Theorem 1.1$\alpha\partial$]{Skopenkov2002} for the DIFF case and \cite[Theorem 1.3$\alpha\partial$]{Skopenkov2002} for the PL case. Usually there exist easier direct proofs | + | We state only the results that can be deduced from the Haefliger-Weber deleted product criterion \cite[$\S$ 5]{Skopenkov2006}, see \cite[6.4]{Haefliger1963}, \cite[Theorem 1.1$\alpha\partial$]{Skopenkov2002} for the DIFF case and \cite[Theorem 1.3$\alpha\partial$]{Skopenkov2002} for the PL case. Usually there exist easier direct proofs than deduction from this criterion. |
| − | Sometimes we give references to direct proofs but we do not claim | + | Sometimes we give references to such direct proofs but we do not claim these are original proofs. |
{{beginthm|Theorem}} | {{beginthm|Theorem}} | ||
Revision as of 13:34, 2 April 2020
|
This page has not been refereed. The information given here might be incomplete or provisional. |
1 Introduction
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3]. In those pages mostly results for closed manifolds are stated.
3]. In those pages mostly results for closed manifolds are stated.
In this page we present results peculiar for manifold with non-empty boundary.
If the category is omitted, then a result stated below holds in both the smooth and piecewise-linear (PL) category.
We state only the results that can be deduced from the Haefliger-Weber deleted product criterion [Skopenkov2006,  5], see [Haefliger1963, 6.4], [Skopenkov2002, Theorem 1.1
5], see [Haefliger1963, 6.4], [Skopenkov2002, Theorem 1.1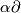 ] for the DIFF case and [Skopenkov2002, Theorem 1.3
] for the DIFF case and [Skopenkov2002, Theorem 1.3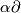 ] for the PL case. Usually there exist easier direct proofs than deduction from this criterion.
Sometimes we give references to such direct proofs but we do not claim these are original proofs.
] for the PL case. Usually there exist easier direct proofs than deduction from this criterion.
Sometimes we give references to such direct proofs but we do not claim these are original proofs.
Theorem 1.1.
Every  -manifold
-manifold  with nonempty boundary PL embeds into
with nonempty boundary PL embeds into 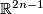 .
.
This result can be found in [Horvatic1971, Theorem 5.2]
2 Unknotting Theorems
Theorem 2.1.
Assume that  is a compact
is a compact  -manifold and either
-manifold and either
(a) 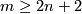 or
or
(b)  is connected and
is connected and 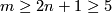 .
.
Then any two embeddings of  into
into  are isotopic.
are isotopic.
The condition (a) stands for General Position Theorem and the condition (b) stands for Whitney-Wu Unknotting Theorem, see Theorems 2.1 and 2.2 respectively of [Skopenkov2016c,  2].
2].
Theorem 2.2.
Assume that  is a compact connected
is a compact connected  -manifold with non-empty boundary and either
-manifold with non-empty boundary and either
(a) 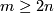 or
or
(b)  is
is  -connected,
-connected, 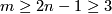 .
.
Then any two embeddings of  into
into  are isotopic.
are isotopic.
Part (a) of this theorem in case  can be found in [Edwards1968,
can be found in [Edwards1968,  4, Corollary 5]. Case
4, Corollary 5]. Case  is clear. Case
is clear. Case  has a short direct proof or can be deduced from Haefliger-Weber deleted product criterion [Skopenkov2006, Theorem 5.5].
has a short direct proof or can be deduced from Haefliger-Weber deleted product criterion [Skopenkov2006, Theorem 5.5].
Theorem 2.2 is a special cases of the following result, see [Zeeman1963, Corollary 2 of Theorem 24 in Chapter 8], [Haefliger1961, Existence Theorem (b) in p. 47].
Theorem 2.3.
Assume that  is a closed
is a closed  -connected
-connected  -manifold. Then for each
-manifold. Then for each 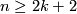 ,
, 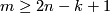 any two embeddings of
any two embeddings of  into
into  are isotopic.
are isotopic.
See Remark 1.2 (d)(ii) of [Skopenkov2016c,  1].
1].
Theorem 2.4.
Assume that  is a
is a  -connected
-connected  -manifold with non-empty boundary.
Then for each
-manifold with non-empty boundary.
Then for each 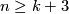 and
and 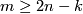 any two embeddings of
any two embeddings of  into
into  are isotopic.
are isotopic.
See also [Hudson1969, Theorem 10.3]
3 References
- [Edwards1968] Edwards, C. H. Unknotting polyhedral homology manifolds, Michigan Math. J. 15 (1968), 81-95. MR226629 Zbl 0167.52001
- [Haefliger1961] A. Haefliger, Plongements différentiables de variétés dans variétés., Comment. Math. Helv.36 (1961), 47-82. MR0145538 (26 #3069) Zbl 0102.38603
- [Haefliger1963] A. Haefliger, Plongements différentiables dans le domain stable., Comment. Math. Helv.37 (1963), 155-176.
- [Horvatic1971] K. Horvatic, On embedding polyhedra and manifolds, Trans. Am. Math. Soc. 157 (1971), 417-436.
- [Hudson1969] J. F. P. Hudson, Piecewise linear topology, W. A. Benjamin, Inc., New York-Amsterdam, 1969. MR0248844 (40 #2094) Zbl 0189.54507
- [Skopenkov2002] A. Skopenkov, On the Haefliger-Hirsch-Wu invariants for embeddings and immersions., Comment. Math. Helv. 77 (2002), no.1, 78-124. MRMR1898394 (2003c:57023) Zbl 1012.57035
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Zeeman1963] E. C. Zeeman, Seminar on Combinatorial Topology, IHES, 1963 (revised 1966).
 3]. In those pages mostly results for closed manifolds are stated.
3]. In those pages mostly results for closed manifolds are stated.
In this page we present results peculiar for manifold with non-empty boundary.
If the category is omitted, then a result stated below holds in both the smooth and piecewise-linear (PL) category.
We state only the results that can be deduced from the Haefliger-Weber deleted product criterion [Skopenkov2006,  5], see [Haefliger1963, 6.4], [Skopenkov2002, Theorem 1.1
5], see [Haefliger1963, 6.4], [Skopenkov2002, Theorem 1.1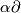 ] for the DIFF case and [Skopenkov2002, Theorem 1.3
] for the DIFF case and [Skopenkov2002, Theorem 1.3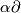 ] for the PL case. Usually there exist easier direct proofs than deduction from this criterion.
Sometimes we give references to such direct proofs but we do not claim these are original proofs.
] for the PL case. Usually there exist easier direct proofs than deduction from this criterion.
Sometimes we give references to such direct proofs but we do not claim these are original proofs.
Theorem 1.1.
Every  -manifold
-manifold  with nonempty boundary PL embeds into
with nonempty boundary PL embeds into 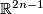 .
.
This result can be found in [Horvatic1971, Theorem 5.2]
2 Unknotting Theorems
Theorem 2.1.
Assume that  is a compact
is a compact  -manifold and either
-manifold and either
(a) 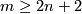 or
or
(b)  is connected and
is connected and 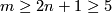 .
.
Then any two embeddings of  into
into  are isotopic.
are isotopic.
The condition (a) stands for General Position Theorem and the condition (b) stands for Whitney-Wu Unknotting Theorem, see Theorems 2.1 and 2.2 respectively of [Skopenkov2016c,  2].
2].
Theorem 2.2.
Assume that  is a compact connected
is a compact connected  -manifold with non-empty boundary and either
-manifold with non-empty boundary and either
(a) 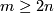 or
or
(b)  is
is  -connected,
-connected, 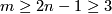 .
.
Then any two embeddings of  into
into  are isotopic.
are isotopic.
Part (a) of this theorem in case  can be found in [Edwards1968,
can be found in [Edwards1968,  4, Corollary 5]. Case
4, Corollary 5]. Case  is clear. Case
is clear. Case  has a short direct proof or can be deduced from Haefliger-Weber deleted product criterion [Skopenkov2006, Theorem 5.5].
has a short direct proof or can be deduced from Haefliger-Weber deleted product criterion [Skopenkov2006, Theorem 5.5].
Theorem 2.2 is a special cases of the following result, see [Zeeman1963, Corollary 2 of Theorem 24 in Chapter 8], [Haefliger1961, Existence Theorem (b) in p. 47].
Theorem 2.3.
Assume that  is a closed
is a closed  -connected
-connected  -manifold. Then for each
-manifold. Then for each 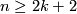 ,
, 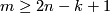 any two embeddings of
any two embeddings of  into
into  are isotopic.
are isotopic.
See Remark 1.2 (d)(ii) of [Skopenkov2016c,  1].
1].
Theorem 2.4.
Assume that  is a
is a  -connected
-connected  -manifold with non-empty boundary.
Then for each
-manifold with non-empty boundary.
Then for each 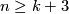 and
and 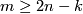 any two embeddings of
any two embeddings of  into
into  are isotopic.
are isotopic.
See also [Hudson1969, Theorem 10.3]
3 References
- [Edwards1968] Edwards, C. H. Unknotting polyhedral homology manifolds, Michigan Math. J. 15 (1968), 81-95. MR226629 Zbl 0167.52001
- [Haefliger1961] A. Haefliger, Plongements différentiables de variétés dans variétés., Comment. Math. Helv.36 (1961), 47-82. MR0145538 (26 #3069) Zbl 0102.38603
- [Haefliger1963] A. Haefliger, Plongements différentiables dans le domain stable., Comment. Math. Helv.37 (1963), 155-176.
- [Horvatic1971] K. Horvatic, On embedding polyhedra and manifolds, Trans. Am. Math. Soc. 157 (1971), 417-436.
- [Hudson1969] J. F. P. Hudson, Piecewise linear topology, W. A. Benjamin, Inc., New York-Amsterdam, 1969. MR0248844 (40 #2094) Zbl 0189.54507
- [Skopenkov2002] A. Skopenkov, On the Haefliger-Hirsch-Wu invariants for embeddings and immersions., Comment. Math. Helv. 77 (2002), no.1, 78-124. MRMR1898394 (2003c:57023) Zbl 1012.57035
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Zeeman1963] E. C. Zeeman, Seminar on Combinatorial Topology, IHES, 1963 (revised 1966).
 3]. In those pages mostly results for closed manifolds are stated.
3]. In those pages mostly results for closed manifolds are stated.
In this page we present results peculiar for manifold with non-empty boundary.
If the category is omitted, then a result stated below holds in both the smooth and piecewise-linear (PL) category.
We state only the results that can be deduced from the Haefliger-Weber deleted product criterion [Skopenkov2006,  5], see [Haefliger1963, 6.4], [Skopenkov2002, Theorem 1.1
5], see [Haefliger1963, 6.4], [Skopenkov2002, Theorem 1.1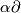 ] for the DIFF case and [Skopenkov2002, Theorem 1.3
] for the DIFF case and [Skopenkov2002, Theorem 1.3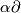 ] for the PL case. Usually there exist easier direct proofs than deduction from this criterion.
Sometimes we give references to such direct proofs but we do not claim these are original proofs.
] for the PL case. Usually there exist easier direct proofs than deduction from this criterion.
Sometimes we give references to such direct proofs but we do not claim these are original proofs.
Theorem 1.1.
Every  -manifold
-manifold  with nonempty boundary PL embeds into
with nonempty boundary PL embeds into 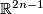 .
.
This result can be found in [Horvatic1971, Theorem 5.2]
2 Unknotting Theorems
Theorem 2.1.
Assume that  is a compact
is a compact  -manifold and either
-manifold and either
(a) 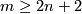 or
or
(b)  is connected and
is connected and 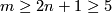 .
.
Then any two embeddings of  into
into  are isotopic.
are isotopic.
The condition (a) stands for General Position Theorem and the condition (b) stands for Whitney-Wu Unknotting Theorem, see Theorems 2.1 and 2.2 respectively of [Skopenkov2016c,  2].
2].
Theorem 2.2.
Assume that  is a compact connected
is a compact connected  -manifold with non-empty boundary and either
-manifold with non-empty boundary and either
(a) 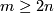 or
or
(b)  is
is  -connected,
-connected, 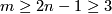 .
.
Then any two embeddings of  into
into  are isotopic.
are isotopic.
Part (a) of this theorem in case  can be found in [Edwards1968,
can be found in [Edwards1968,  4, Corollary 5]. Case
4, Corollary 5]. Case  is clear. Case
is clear. Case  has a short direct proof or can be deduced from Haefliger-Weber deleted product criterion [Skopenkov2006, Theorem 5.5].
has a short direct proof or can be deduced from Haefliger-Weber deleted product criterion [Skopenkov2006, Theorem 5.5].
Theorem 2.2 is a special cases of the following result, see [Zeeman1963, Corollary 2 of Theorem 24 in Chapter 8], [Haefliger1961, Existence Theorem (b) in p. 47].
Theorem 2.3.
Assume that  is a closed
is a closed  -connected
-connected  -manifold. Then for each
-manifold. Then for each 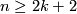 ,
, 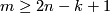 any two embeddings of
any two embeddings of  into
into  are isotopic.
are isotopic.
See Remark 1.2 (d)(ii) of [Skopenkov2016c,  1].
1].
Theorem 2.4.
Assume that  is a
is a  -connected
-connected  -manifold with non-empty boundary.
Then for each
-manifold with non-empty boundary.
Then for each 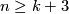 and
and 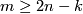 any two embeddings of
any two embeddings of  into
into  are isotopic.
are isotopic.
See also [Hudson1969, Theorem 10.3]
3 References
- [Edwards1968] Edwards, C. H. Unknotting polyhedral homology manifolds, Michigan Math. J. 15 (1968), 81-95. MR226629 Zbl 0167.52001
- [Haefliger1961] A. Haefliger, Plongements différentiables de variétés dans variétés., Comment. Math. Helv.36 (1961), 47-82. MR0145538 (26 #3069) Zbl 0102.38603
- [Haefliger1963] A. Haefliger, Plongements différentiables dans le domain stable., Comment. Math. Helv.37 (1963), 155-176.
- [Horvatic1971] K. Horvatic, On embedding polyhedra and manifolds, Trans. Am. Math. Soc. 157 (1971), 417-436.
- [Hudson1969] J. F. P. Hudson, Piecewise linear topology, W. A. Benjamin, Inc., New York-Amsterdam, 1969. MR0248844 (40 #2094) Zbl 0189.54507
- [Skopenkov2002] A. Skopenkov, On the Haefliger-Hirsch-Wu invariants for embeddings and immersions., Comment. Math. Helv. 77 (2002), no.1, 78-124. MRMR1898394 (2003c:57023) Zbl 1012.57035
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Zeeman1963] E. C. Zeeman, Seminar on Combinatorial Topology, IHES, 1963 (revised 1966).