Embeddings of manifolds with boundary: classification
m (→Unknotting Theorems) |
m (→Unknotting Theorems) |
||
| Line 24: | Line 24: | ||
== Unknotting Theorems == | == Unknotting Theorems == | ||
<wikitex>; | <wikitex>; | ||
| + | |||
| + | If the category is omitted, then a result stated below holds in both the smooth and piecewise-linear (PL) category. | ||
{{beginthm|Theorem}}\label{th::unknotting} | {{beginthm|Theorem}}\label{th::unknotting} | ||
| − | Assume $N$ is a compact connected $n$-manifold and | + | Assume $N$ is a compact connected $n$-manifold and either |
| − | + | <!--(a) \label{item_GP} (General position theorem)--> | |
| − | (a) \label{item_GP} (General position theorem) | + | $m \ge 2n+2$ or |
| − | $m \ge 2n+2$ | + | <!--(b) \label{item_WW} (Whitney-Wu unknotting theorem)--> |
| − | + | $m\ge2n+1\ge5$. | |
| − | (b) \label{item_WW} (Whitney-Wu unknotting theorem) | + | |
| − | $m\ge2n+1\ge5$ | + | |
| − | + | ||
Then any two embeddings of $N$ into $\R^m$ are isotopic. | Then any two embeddings of $N$ into $\R^m$ are isotopic. | ||
{{endthm}} | {{endthm}} | ||
| + | Condition $m \ge 2n+2$ stands for General Position Theorem and condition $m\ge2n+1\ge5$ stands for Whitney-Wu Unknotting Theorem, see [[Embeddings_in_Euclidean_space:_an_introduction_to_their_classification#Unknotting theorems|Unknotting Theorems]], theprems 2.1 and 2.2 respectivly. | ||
{{beginthm|Theorem}} | {{beginthm|Theorem}} | ||
| Line 45: | Line 45: | ||
Assume $N$ is a compact connected $n$-manifold with non-empty boundary and one of the following conditions holds: | Assume $N$ is a compact connected $n$-manifold with non-empty boundary and one of the following conditions holds: | ||
| − | (a) | + | (a) $m \ge 2n\neq4$ |
| − | $m \ge 2n\neq4$ | + | |
| − | (b) | + | (b) $N$ is $1$-connected, $m \ge 2n - 1\ge3$ |
| − | $N$ is $1$-connected, $m \ge 2n - 1\ge3 | + | |
Then any two embeddings of $N$ into $\R^m$ are isotopic. | Then any two embeddings of $N$ into $\R^m$ are isotopic. | ||
{{endthm}} | {{endthm}} | ||
| − | Part (a) of this theorem can be found in \cite[$\S$ 4, corollary 5]{Edwards1968} | + | Part (a) of this theorem in case $n>2$ can be found in \cite[$\S$ 4, corollary 5]{Edwards1968}. Case $n=1$ is clear. Case $n=2$ can be derived from deleted square criterion. |
{{beginthm|Theorem}} | {{beginthm|Theorem}} | ||
| − | + | [The Haefliger-Zeeman unknotting theorem] | |
| + | For every $n\ge2k + 2$, $m \ge 2n - k + 1$ and closed $k$-connected $n$-manifold $N$, any two embeddings of $N$ into $\R^m$ are isotopic. | ||
{{endthm}} | {{endthm}} | ||
| − | |||
| − | |||
{{beginthm|Theorem}} | {{beginthm|Theorem}} | ||
| − | + | Assume $N$ is a compact $n$-manifold, $\partial N\neq\emptyset$. If $N$ is $k$-connected, $m\ge2n-k$ and $m-k>3$ then any two embeddings of $N$ into $\R^m$ are isotopic. | |
| − | + | <!--Let $f, g\colon N \to \R^q$ be PL-embeddings, $q-n > 3$. Suppose $(N, \partial N)$ is $(2n-q)$-connected. Then $f$ and $g$ are isotopic.--> | |
{{endthm}} | {{endthm}} | ||
| + | |||
| + | This result can be found in \cite[Theorem 10.3]{Hudson1969} | ||
</wikitex> | </wikitex> | ||
Revision as of 16:41, 22 March 2020
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
Most of this page is intended not only for specialists in embeddings, but also for mathematician from other areas who want to apply or to learn the theory of embeddings.
Recall that some Unknotting Theorems hold for manifolds with boundary [Skopenkov2016c,  3], [Skopenkov2006,
3], [Skopenkov2006,  2]. In this page we present results peculiar for manifold with non-empty boundary.
2]. In this page we present results peculiar for manifold with non-empty boundary.
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3].
3].
2 Unknotting Theorems
If the category is omitted, then a result stated below holds in both the smooth and piecewise-linear (PL) category.
Theorem 2.1.
Assume  is a compact connected
is a compact connected  -manifold and either
-manifold and either
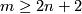 or
or
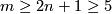 .
Then any two embeddings of
.
Then any two embeddings of  into
into  are isotopic.
are isotopic.
Condition 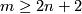 stands for General Position Theorem and condition
stands for General Position Theorem and condition 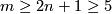 stands for Whitney-Wu Unknotting Theorem, see Unknotting Theorems, theprems 2.1 and 2.2 respectivly.
stands for Whitney-Wu Unknotting Theorem, see Unknotting Theorems, theprems 2.1 and 2.2 respectivly.
Theorem 2.2.
Every  -manifold
-manifold  with nonempty boundary PL-embeds into
with nonempty boundary PL-embeds into 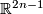 .
.
This result can be found in [Horvatic1971, theorem 5.2]
Theorem 2.3.
Assume  is a compact connected
is a compact connected  -manifold with non-empty boundary and one of the following conditions holds:
-manifold with non-empty boundary and one of the following conditions holds:
(a) 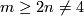
(b)  is
is  -connected,
-connected, 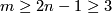
Then any two embeddings of  into
into  are isotopic.
are isotopic.
Part (a) of this theorem in case 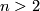 can be found in [Edwards1968,
can be found in [Edwards1968,  4, corollary 5]. Case
4, corollary 5]. Case  is clear. Case
is clear. Case  can be derived from deleted square criterion.
can be derived from deleted square criterion.
Theorem 2.4.
[The Haefliger-Zeeman unknotting theorem]
For every 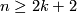 ,
, 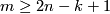 and closed
and closed  -connected
-connected  -manifold
-manifold  , any two embeddings of
, any two embeddings of  into
into  are isotopic.
are isotopic.
Theorem 2.5.
Assume  is a compact
is a compact  -manifold,
-manifold, 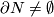 . If
. If  is
is  -connected,
-connected, 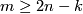 and
and 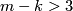 then any two embeddings of
then any two embeddings of  into
into  are isotopic.
are isotopic.
This result can be found in [Hudson1969, Theorem 10.3]
3 Construction and examples
...
4 Invariants
...
5 Classification
Theorem 5.1.[Becker-Glover]
Let  be a closed homologically
be a closed homologically  -connected
-connected  -manifold
and
-manifold
and 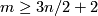 .
The cone map
.
The cone map 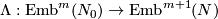 is one-to-one
for
is one-to-one
for
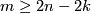 and is surjective
for
and is surjective
for 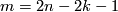 .
.
6 Further discussion
...
7 References
- [Becker&Glover1971] J. Becker and H. Glover, Note on the embedding of manifolds in Euclidean space, Proc. Am. Math. Soc. 27 (1971), 405-410. MR0268903 (42 #3800) Zbl 0207.22402
- [Edwards1968] Edwards, C. H. Unknotting polyhedral homology manifolds, Michigan Math. J. 15 (1968), 81-95. MR226629 Zbl 0167.52001
- [Horvatic1971] K. Horvatic, On embedding polyhedra and manifolds, Trans. Am. Math. Soc. 157 (1971), 417-436.
- [Hudson1969] J. F. P. Hudson, Piecewise linear topology, W. A. Benjamin, Inc., New York-Amsterdam, 1969. MR0248844 (40 #2094) Zbl 0189.54507
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
 2]. In this page we present results peculiar for manifold with non-empty boundary.
2]. In this page we present results peculiar for manifold with non-empty boundary.
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3].
3].
2 Unknotting Theorems
If the category is omitted, then a result stated below holds in both the smooth and piecewise-linear (PL) category.
Theorem 2.1.
Assume  is a compact connected
is a compact connected  -manifold and either
-manifold and either
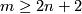 or
or
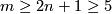 .
Then any two embeddings of
.
Then any two embeddings of  into
into  are isotopic.
are isotopic.
Condition 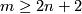 stands for General Position Theorem and condition
stands for General Position Theorem and condition 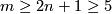 stands for Whitney-Wu Unknotting Theorem, see Unknotting Theorems, theprems 2.1 and 2.2 respectivly.
stands for Whitney-Wu Unknotting Theorem, see Unknotting Theorems, theprems 2.1 and 2.2 respectivly.
Theorem 2.2.
Every  -manifold
-manifold  with nonempty boundary PL-embeds into
with nonempty boundary PL-embeds into 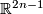 .
.
This result can be found in [Horvatic1971, theorem 5.2]
Theorem 2.3.
Assume  is a compact connected
is a compact connected  -manifold with non-empty boundary and one of the following conditions holds:
-manifold with non-empty boundary and one of the following conditions holds:
(a) 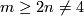
(b)  is
is  -connected,
-connected, 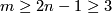
Then any two embeddings of  into
into  are isotopic.
are isotopic.
Part (a) of this theorem in case 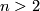 can be found in [Edwards1968,
can be found in [Edwards1968,  4, corollary 5]. Case
4, corollary 5]. Case  is clear. Case
is clear. Case  can be derived from deleted square criterion.
can be derived from deleted square criterion.
Theorem 2.4.
[The Haefliger-Zeeman unknotting theorem]
For every 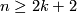 ,
, 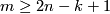 and closed
and closed  -connected
-connected  -manifold
-manifold  , any two embeddings of
, any two embeddings of  into
into  are isotopic.
are isotopic.
Theorem 2.5.
Assume  is a compact
is a compact  -manifold,
-manifold, 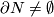 . If
. If  is
is  -connected,
-connected, 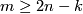 and
and 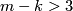 then any two embeddings of
then any two embeddings of  into
into  are isotopic.
are isotopic.
This result can be found in [Hudson1969, Theorem 10.3]
3 Construction and examples
...
4 Invariants
...
5 Classification
Theorem 5.1.[Becker-Glover]
Let  be a closed homologically
be a closed homologically  -connected
-connected  -manifold
and
-manifold
and 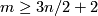 .
The cone map
.
The cone map 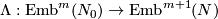 is one-to-one
for
is one-to-one
for
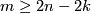 and is surjective
for
and is surjective
for 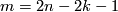 .
.
6 Further discussion
...
7 References
- [Becker&Glover1971] J. Becker and H. Glover, Note on the embedding of manifolds in Euclidean space, Proc. Am. Math. Soc. 27 (1971), 405-410. MR0268903 (42 #3800) Zbl 0207.22402
- [Edwards1968] Edwards, C. H. Unknotting polyhedral homology manifolds, Michigan Math. J. 15 (1968), 81-95. MR226629 Zbl 0167.52001
- [Horvatic1971] K. Horvatic, On embedding polyhedra and manifolds, Trans. Am. Math. Soc. 157 (1971), 417-436.
- [Hudson1969] J. F. P. Hudson, Piecewise linear topology, W. A. Benjamin, Inc., New York-Amsterdam, 1969. MR0248844 (40 #2094) Zbl 0189.54507
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
 2]. In this page we present results peculiar for manifold with non-empty boundary.
2]. In this page we present results peculiar for manifold with non-empty boundary.
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3].
3].
2 Unknotting Theorems
If the category is omitted, then a result stated below holds in both the smooth and piecewise-linear (PL) category.
Theorem 2.1.
Assume  is a compact connected
is a compact connected  -manifold and either
-manifold and either
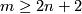 or
or
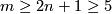 .
Then any two embeddings of
.
Then any two embeddings of  into
into  are isotopic.
are isotopic.
Condition 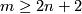 stands for General Position Theorem and condition
stands for General Position Theorem and condition 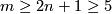 stands for Whitney-Wu Unknotting Theorem, see Unknotting Theorems, theprems 2.1 and 2.2 respectivly.
stands for Whitney-Wu Unknotting Theorem, see Unknotting Theorems, theprems 2.1 and 2.2 respectivly.
Theorem 2.2.
Every  -manifold
-manifold  with nonempty boundary PL-embeds into
with nonempty boundary PL-embeds into 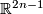 .
.
This result can be found in [Horvatic1971, theorem 5.2]
Theorem 2.3.
Assume  is a compact connected
is a compact connected  -manifold with non-empty boundary and one of the following conditions holds:
-manifold with non-empty boundary and one of the following conditions holds:
(a) 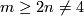
(b)  is
is  -connected,
-connected, 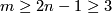
Then any two embeddings of  into
into  are isotopic.
are isotopic.
Part (a) of this theorem in case 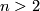 can be found in [Edwards1968,
can be found in [Edwards1968,  4, corollary 5]. Case
4, corollary 5]. Case  is clear. Case
is clear. Case  can be derived from deleted square criterion.
can be derived from deleted square criterion.
Theorem 2.4.
[The Haefliger-Zeeman unknotting theorem]
For every 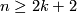 ,
, 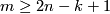 and closed
and closed  -connected
-connected  -manifold
-manifold  , any two embeddings of
, any two embeddings of  into
into  are isotopic.
are isotopic.
Theorem 2.5.
Assume  is a compact
is a compact  -manifold,
-manifold, 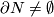 . If
. If  is
is  -connected,
-connected, 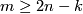 and
and 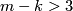 then any two embeddings of
then any two embeddings of  into
into  are isotopic.
are isotopic.
This result can be found in [Hudson1969, Theorem 10.3]
3 Construction and examples
...
4 Invariants
...
5 Classification
Theorem 5.1.[Becker-Glover]
Let  be a closed homologically
be a closed homologically  -connected
-connected  -manifold
and
-manifold
and 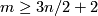 .
The cone map
.
The cone map 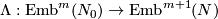 is one-to-one
for
is one-to-one
for
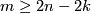 and is surjective
for
and is surjective
for 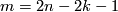 .
.
6 Further discussion
...
7 References
- [Becker&Glover1971] J. Becker and H. Glover, Note on the embedding of manifolds in Euclidean space, Proc. Am. Math. Soc. 27 (1971), 405-410. MR0268903 (42 #3800) Zbl 0207.22402
- [Edwards1968] Edwards, C. H. Unknotting polyhedral homology manifolds, Michigan Math. J. 15 (1968), 81-95. MR226629 Zbl 0167.52001
- [Horvatic1971] K. Horvatic, On embedding polyhedra and manifolds, Trans. Am. Math. Soc. 157 (1971), 417-436.
- [Hudson1969] J. F. P. Hudson, Piecewise linear topology, W. A. Benjamin, Inc., New York-Amsterdam, 1969. MR0248844 (40 #2094) Zbl 0189.54507
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.