Embeddings just below the stable range: classification
| Line 6: | Line 6: | ||
{{beginthm|Classification Theorem}}\label{th4} | {{beginthm|Classification Theorem}}\label{th4} | ||
Let $N$ be a closed connected $n$-manifold. The Whitney invariant | Let $N$ be a closed connected $n$-manifold. The Whitney invariant | ||
| − | $$W:E^{2n}(N)\to \ | + | $$W:E^{2n}(N)\to\left\{\begin{array}{cc} H_1(N;\Zz_{(n-1)})& |
| − | \ | + | \mbox{either $n$ is odd or $N$ is orientable}\\ |
| − | \Zz\oplus\Zz_2^{s-1}&\ | + | \Zz\oplus\Zz_2^{s-1}&\mbox{$n$ is even, $N$ is non-orientable and } |
| − | H_1(N,\zZ_2)\cong\Zz_2^s,\ | + | H_1(N,\zZ_2)\cong\Zz_2^s,\end{array}\right$$ |
is bijective if either $n\ge4$ or $n=3$ and CAT=PL \cite{HaefligerHirsch1963}, \cite{Bausum75}, \cite{Vrabec77}, cf. \cite{Hudson1969} | is bijective if either $n\ge4$ or $n=3$ and CAT=PL \cite{HaefligerHirsch1963}, \cite{Bausum75}, \cite{Vrabec77}, cf. \cite{Hudson1969} | ||
{{endthm}} | {{endthm}} | ||
| Line 19: | Line 19: | ||
<wikitex>; | <wikitex>; | ||
| − | Fix orientations on $\ | + | Fix orientations on $\Rr^{2n}$ and, if $N$ is even, on $N$. Fix an embedding $f_0:N\to\Rr^{2n}$. For an embedding $f:N\to\Rr^{2n}$ |
| − | the restrictions of $f$ and $f_0$ to $N_0$ are regular homotopic \cite{ | + | the restrictions of $f$ and $f_0$ to $N_0$ are regular homotopic \cite{Hirsch1959}. Since $N_0$ has an $(n-1)$-dimensional spine, it follows that these restrictions are isotopic, cf. \cite{HaefligerHirsch1963}, 3.1.b, \cite{Takase2006}, Lemma 2.2. So we can make an isotopy of $f$ and assume that $f=f_0$ on $N_0$. Take a general position homotopy $F:B^n\times I\to\Rr^{2n}$ relative to |
$\partial B^n$ between the restrictions of $f$ and $g$ to $B^n$. Then $f\cap F:=(f|_{N-B^n})^{-1}F(B^n\times I)$ (i.e. `the intersection of this homotopy with $f(N-B^n)$') is a 1-manifold (possibly non-compact) without boundary. Define $W(f)$ to be the homology class of the closure of this 1-manifold: | $\partial B^n$ between the restrictions of $f$ and $g$ to $B^n$. Then $f\cap F:=(f|_{N-B^n})^{-1}F(B^n\times I)$ (i.e. `the intersection of this homotopy with $f(N-B^n)$') is a 1-manifold (possibly non-compact) without boundary. Define $W(f)$ to be the homology class of the closure of this 1-manifold: | ||
| − | $$W(f):=[ | + | $$W(f):=[Cl(f\cap F)]\in H_1(N_0,\partial N_0;\Zz_{(n)})\cong H_1(N;\Zz_{(n)}).$$ |
The orientation on $f\cap F$ is defined for $N$ orientable as follows. (This orientation is defined for each $n$ but used only for odd $n$.) For each point $x\in f\cap F$ take a vector at $x$ tangent to $f\cap F$. Complete this vector to a positive base tangent to $N$. Since $n+2(n+1)>2\cdot2n$, by general position there is a unique point $y\in B^n\times I$ such that $Fy=fx$. The tangent vector at $x$ thus gives a tangent vector at $y$ to $B^n\times I$. Complete this vector to a positive base tangent to $B^n\times I$, where the orientation on $B^n$ comes from $N$. The union of the images of the constructed two bases is a base at $Fy=fx$ of $\Rr^{2n}$. If this base is positive, then call the initial vector of $f\cap F$ positive. Since a change of the orientation on $f\cap F$ forces a change of the orientation of the latter base of $\Rr^{2n}$, it follows that this condition indeed defines an orientation on $f\cap F$. | The orientation on $f\cap F$ is defined for $N$ orientable as follows. (This orientation is defined for each $n$ but used only for odd $n$.) For each point $x\in f\cap F$ take a vector at $x$ tangent to $f\cap F$. Complete this vector to a positive base tangent to $N$. Since $n+2(n+1)>2\cdot2n$, by general position there is a unique point $y\in B^n\times I$ such that $Fy=fx$. The tangent vector at $x$ thus gives a tangent vector at $y$ to $B^n\times I$. Complete this vector to a positive base tangent to $B^n\times I$, where the orientation on $B^n$ comes from $N$. The union of the images of the constructed two bases is a base at $Fy=fx$ of $\Rr^{2n}$. If this base is positive, then call the initial vector of $f\cap F$ positive. Since a change of the orientation on $f\cap F$ forces a change of the orientation of the latter base of $\Rr^{2n}$, it follows that this condition indeed defines an orientation on $f\cap F$. | ||
{{beginthm|Remark}}\label{re5} | {{beginthm|Remark}}\label{re5} | ||
| − | *The Whitney invariant is well-defined, i.e. independent of the choice of $F$ and of the isotopy making $f=f_0$ outside $B^n$. This is so because the above definition is clearly equivalent to the following: $W(f)$ is the homology class of the algebraic sum of the top-dimensional simplices of the self-intersection set $\Sigma(H):=Cl\{x\in N\times I\ |\ \#H^{-1}Hx>1\}$ of a general position homotopy $H$ between $f$ and $f_0$. | + | *The Whitney invariant is well-defined, i.e. independent of the choice of $F$ and of the isotopy making $f=f_0$ outside $B^n$. This is so because the above definition is clearly equivalent to the following: $W(f)$ is the homology class of the algebraic sum of the top-dimensional simplices of the self-intersection set $\Sigma(H):=Cl\{x\in N\times I\ |\ \#H^{-1}Hx>1\}$ of a general position homotopy $H$ between $f$ and $f_0$. (For details and definition of the signs of the simplices see \cite{Hudson1969}, \S12, \cite{Vrabec1977}, p. 145, \cite{Skopenkov2006}, \S2, \cite{Skopenkov2010}.) It is for being well-defined that we need $\Zz_2$-coefficients when $n$ is even. |
| − | (For details and definition of the signs of the simplices see \cite{Hudson1969}, \S12, \cite{Vrabec1977}, p. 145, \cite{Skopenkov2006}, \S2, \cite{Skopenkov2010}.) | + | |
| − | It is for being well-defined that we need $\Zz_2$-coefficients when $n$ is even. | + | |
*Clearly, $W(f_0)=0$. The definition of $W$ depends on the choice of $f_0$, but we write $W$ not $W_{f_0}$ for brevity. | *Clearly, $W(f_0)=0$. The definition of $W$ depends on the choice of $f_0$, but we write $W$ not $W_{f_0}$ for brevity. | ||
*Since a change of the orientation on $N$ forces a change of the orientation on $B^n$, the class $W(f)$ is independent of the choice of the orientation on $N$. For the reflection $\sigma:\Rr^{2n}\to\Rr^{2n}$ with respect to a hyperplane we have $W(\sigma\circ f)=-W(f)$ (because we may assume that $f=f_0=\sigma\circ f$ on $N_0$ and because a change of the orientation of $\Rr^{2n}$ forces a change of the orientation of $f\cap F$). | *Since a change of the orientation on $N$ forces a change of the orientation on $B^n$, the class $W(f)$ is independent of the choice of the orientation on $N$. For the reflection $\sigma:\Rr^{2n}\to\Rr^{2n}$ with respect to a hyperplane we have $W(\sigma\circ f)=-W(f)$ (because we may assume that $f=f_0=\sigma\circ f$ on $N_0$ and because a change of the orientation of $\Rr^{2n}$ forces a change of the orientation of $f\cap F$). | ||
| Line 38: | Line 36: | ||
</wikitex> | </wikitex> | ||
| − | == Construction of the embedding <wikitex> | + | == Construction of the embedding <wikitex> $f_a:N\to\Rr^{2n}$ from an embedding |
| − | $f_0:N\to\ | + | $f_0:N\to\Rr^{2n}$ and $a\in H_1(N)$ (for orientable $N$ and $n\ge3$) </wikitex>== |
<wikitex>; | <wikitex>; | ||
| Line 46: | Line 44: | ||
Take a vector field on $S^1\times*$ normal to $S^1\times S^{n-1}$. Extend $S^1\times*$ along this vector field to a smooth map | Take a vector field on $S^1\times*$ normal to $S^1\times S^{n-1}$. Extend $S^1\times*$ along this vector field to a smooth map | ||
| − | $\overline a:D^2\to S^{2n}$. Since $2n>4$ and $n+2<2n$, by general position we may assume that $\overline a$ is an embedding and $\overline a( | + | $\overline a:D^2\to S^{2n}$. Since $2n>4$ and $n+2<2n$, by general position we may assume that $\overline a$ is an embedding and $\overline a(Int D^2)$ misses $f_0(N)\cup S^1\times S^{n-1}$. Since $n-1>1$, we have $\pi_1(V_{2n-2,n-1})=0$. |
Hence the standard framing of $S^1\times*$ in $S^1\times S^{n-1}$ extends to an $(n-1)$-framing on $\overline a(D^2)$ in $\Rr^{2n}$. | Hence the standard framing of $S^1\times*$ in $S^1\times S^{n-1}$ extends to an $(n-1)$-framing on $\overline a(D^2)$ in $\Rr^{2n}$. | ||
Thus $\overline a$ extends to an embedding | Thus $\overline a$ extends to an embedding | ||
$$\widehat a:D^2\times D^{n-1}\to C_{f_0}\quad\text{such that}\quad | $$\widehat a:D^2\times D^{n-1}\to C_{f_0}\quad\text{such that}\quad | ||
\widehat a(\partial D^2\times D^{n-1})\subset S^1\times S^{n-1}$$ | \widehat a(\partial D^2\times D^{n-1})\subset S^1\times S^{n-1}$$ | ||
| − | $$\ | + | $$\mbox{Let}\qquad |
\Sigma:\ =\ S^1\times S^{n-1}-\widehat a(\partial D^2\times\Int D^{n-1}) | \Sigma:\ =\ S^1\times S^{n-1}-\widehat a(\partial D^2\times\Int D^{n-1}) | ||
\bigcup\limits_{\widehat a(\partial D^2\times\partial D^{n-1})} | \bigcup\limits_{\widehat a(\partial D^2\times\partial D^{n-1})} | ||
| Line 57: | Line 55: | ||
Note that | Note that | ||
* This construction generalizes the construction of $\Hud_n(a)$ (from $\Hud_n(0)$). | * This construction generalizes the construction of $\Hud_n(a)$ (from $\Hud_n(0)$). | ||
| − | * Clearly, $W(f_a)$ is $a$ or $a\mod2$. Thus all isotopy classes of embedings $N\to\Rr^{2n}$ can be obtained (from a certain given embedding $f_0$) by the above construction. Hence unless $n=3$ and CAT=DIFF, the above construction defines an action | + | * Clearly, $W(f_a)$ is $a$ or $a\mod2$. Thus all isotopy classes of embedings $N\to\Rr^{2n}$ can be obtained (from a certain given embedding $f_0$) by the above construction. Hence unless $n=3$ and CAT=DIFF, the above construction defines an action $H_1(N;\Zz_{(n-1)})\to E^{2n}(N)$. |
| − | $H_1(N;\Zz_{(n-1)})\to E^{2n}(N)$. | + | |
</wikitex> | </wikitex> | ||
Revision as of 15:49, 14 February 2010
| This page has been accepted for publication in the Bulletin of the Manifold Atlas. |
Contents |
1 Introduction
For notation and conventions see high codimension embeddings.
Classification Theorem 1.1.
Let  be a closed connected
be a closed connected  -manifold. The Whitney invariant
-manifold. The Whitney invariant
Tex syntax error
is bijective if either  or
or  and CAT=PL [HaefligerHirsch1963], [Bausum75], [Vrabec77], cf. [Hudson1969]
and CAT=PL [HaefligerHirsch1963], [Bausum75], [Vrabec77], cf. [Hudson1969]
Classification of smooth embeddings of 3-manifolds in the 6-space is more complicated.
2 Definition of the Whitney invariant (for either n odd or N orientable)
Fix orientations on 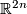 and, if
and, if  is even, on
is even, on  . Fix an embedding
. Fix an embedding 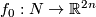 . For an embedding
. For an embedding 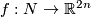 the restrictions of
the restrictions of  and
and  to
to  are regular homotopic [Hirsch1959]. Since
are regular homotopic [Hirsch1959]. Since  has an
has an  -dimensional spine, it follows that these restrictions are isotopic, cf. [HaefligerHirsch1963], 3.1.b, [Takase2006], Lemma 2.2. So we can make an isotopy of
-dimensional spine, it follows that these restrictions are isotopic, cf. [HaefligerHirsch1963], 3.1.b, [Takase2006], Lemma 2.2. So we can make an isotopy of  and assume that
and assume that  on
on  . Take a general position homotopy
. Take a general position homotopy 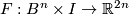 relative to
relative to
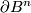 between the restrictions of
between the restrictions of  and
and  to
to  . Then
. Then 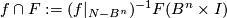 (i.e. `the intersection of this homotopy with
(i.e. `the intersection of this homotopy with 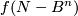 ') is a 1-manifold (possibly non-compact) without boundary. Define
') is a 1-manifold (possibly non-compact) without boundary. Define  to be the homology class of the closure of this 1-manifold:
to be the homology class of the closure of this 1-manifold:
![\displaystyle W(f):=[Cl(f\cap F)]\in H_1(N_0,\partial N_0;\Zz_{(n)})\cong H_1(N;\Zz_{(n)}).](/images/math/2/b/b/2bbc331d0f1495918467d3ff52161652.png)
The orientation on  is defined for
is defined for  orientable as follows. (This orientation is defined for each
orientable as follows. (This orientation is defined for each  but used only for odd
but used only for odd  .) For each point
.) For each point 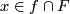 take a vector at
take a vector at  tangent to
tangent to  . Complete this vector to a positive base tangent to
. Complete this vector to a positive base tangent to  . Since
. Since 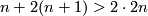 , by general position there is a unique point
, by general position there is a unique point 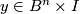 such that
such that 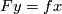 . The tangent vector at
. The tangent vector at  thus gives a tangent vector at
thus gives a tangent vector at  to
to 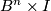 . Complete this vector to a positive base tangent to
. Complete this vector to a positive base tangent to 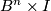 , where the orientation on
, where the orientation on  comes from
comes from  . The union of the images of the constructed two bases is a base at
. The union of the images of the constructed two bases is a base at 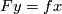 of
of 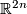 . If this base is positive, then call the initial vector of
. If this base is positive, then call the initial vector of  positive. Since a change of the orientation on
positive. Since a change of the orientation on  forces a change of the orientation of the latter base of
forces a change of the orientation of the latter base of 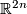 , it follows that this condition indeed defines an orientation on
, it follows that this condition indeed defines an orientation on  .
.
Remark 2.1.
- The Whitney invariant is well-defined, i.e. independent of the choice of
 and of the isotopy making
and of the isotopy making  outside
outside  . This is so because the above definition is clearly equivalent to the following:
. This is so because the above definition is clearly equivalent to the following:  is the homology class of the algebraic sum of the top-dimensional simplices of the self-intersection set
is the homology class of the algebraic sum of the top-dimensional simplices of the self-intersection set 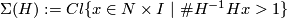 of a general position homotopy
of a general position homotopy  between
between  and
and  . (For details and definition of the signs of the simplices see [Hudson1969], \S12, [Vrabec1977], p. 145, [Skopenkov2006], \S2, [Skopenkov2010].) It is for being well-defined that we need
. (For details and definition of the signs of the simplices see [Hudson1969], \S12, [Vrabec1977], p. 145, [Skopenkov2006], \S2, [Skopenkov2010].) It is for being well-defined that we need  -coefficients when
-coefficients when  is even.
is even.
- Clearly,
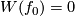 . The definition of
. The definition of Tex syntax error
depends on the choice of , but we write
, but we write Tex syntax error
not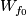 for brevity.
for brevity.
- Since a change of the orientation on
 forces a change of the orientation on
forces a change of the orientation on  , the class
, the class  is independent of the choice of the orientation on
is independent of the choice of the orientation on  . For the reflection
. For the reflection 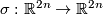 with respect to a hyperplane we have
with respect to a hyperplane we have 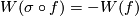 (because we may assume that
(because we may assume that 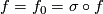 on
on  and because a change of the orientation of
and because a change of the orientation of 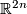 forces a change of the orientation of
forces a change of the orientation of  ).
).
- The above definition makes sense for each
 , not only for
, not only for  .
.
- Clearly,
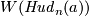 is
is  or
or  for
for 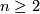 for the Hudson tori.
for the Hudson tori.
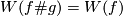 for each embeddings
for each embeddings 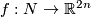 and
and 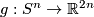 .
.
Construction of the embedding f a:N\to\Rr^{2n} from an embedding
f 0:N\to\Rr^{2n} and a\in H 1(N) (for orientable N and n\ge3) 3 Construction of the embedding 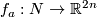 from an embedding
from an embedding
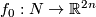 and
and 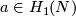 (for orientable
(for orientable  and
and  )
)
Represent  by an embedding
by an embedding 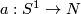 . Since any orientable bundle over
. Since any orientable bundle over  is trivial,
is trivial, 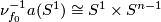 . Identify
. Identify 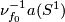 with
with  . It remains to make an embedded surgery of
. It remains to make an embedded surgery of
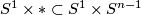 to obtain an
to obtain an  -sphere
-sphere 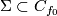 , and then we set
, and then we set 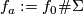 .
.
Take a vector field on 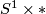 normal to
normal to  . Extend
. Extend 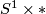 along this vector field to a smooth map
along this vector field to a smooth map
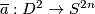 . Since
. Since 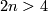 and
and 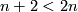 , by general position we may assume that
, by general position we may assume that 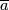 is an embedding and
is an embedding and 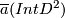 misses
misses 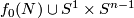 . Since
. Since 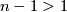 , we have
, we have 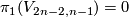 .
Hence the standard framing of
.
Hence the standard framing of 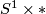 in
in  extends to an
extends to an  -framing on
-framing on 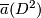 in
in 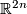 .
Thus
.
Thus 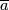 extends to an embedding
extends to an embedding

Tex syntax error
Note that
- This construction generalizes the construction of
 (from
(from 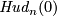 ).
).
- Clearly,
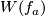 is
is  or
or  . Thus all isotopy classes of embedings
. Thus all isotopy classes of embedings 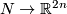 can be obtained (from a certain given embedding
can be obtained (from a certain given embedding  ) by the above construction. Hence unless
) by the above construction. Hence unless  and CAT=DIFF, the above construction defines an action
and CAT=DIFF, the above construction defines an action 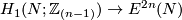 .
.
4 References
- [Bausum75] Template:Bausum75
- [HaefligerHirsch1963] Template:HaefligerHirsch1963
- [Hirsch1959] M. W. Hirsch, Immersions of manifolds, Trans. Amer. Math. Soc. 93 (1959), 242–276. MR0119214 (22 #9980) Zbl 0118.18603
- [Hudson1969] J. F. P. Hudson, Piecewise linear topology, W. A. Benjamin, Inc., New York-Amsterdam, 1969. MR0248844 (40 #2094) Zbl 0189.54507
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2010] A. Skopenkov, Embeddings of k-connected n-manifolds into
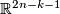 , Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
, Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
- [Takase2006] M. Takase, Homology 3-spheres in codimension three, Internat. J. Math. 17 (2006), no.8, 869–885.
arxiv:math/0506464 MR2261638 (2007g:57049) Zbl 1113.57013
- [Vrabec1977] J. Vrabec, Knotting a
 -connected closed
-connected closed 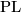
 -manifold in
-manifold in 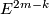 , Trans. Amer. Math. Soc. 233 (1977), 137–165. MR0645405 (58 #31097) Zbl 386.57013
, Trans. Amer. Math. Soc. 233 (1977), 137–165. MR0645405 (58 #31097) Zbl 386.57013
- [Vrabec77] Template:Vrabec77
|
This page has not been refereed. The information given here might be incomplete or provisional. |