Knotted tori
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
1 Introduction
Many interesting examples of embeddings are embeddings 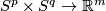 , i.e. knotted tori. See Hudson tori, [Alexander1924], [Milgram&Rees1971], [Kosinski1961], [Hudson1963], [Wall1965], [Tindell1969], [Boechat&Haefliger1970], [Boechat1971], [Milgram&Rees1971], [Lucas&Saeki2002], [Skopenkov2002]. A classification of knotted tori is a natural next step (after the link theory [Haefliger1966a] and the classification of embeddings of highly-connected manifolds) towards classification of embeddings of arbitrary manifolds. Since the general Knotting Problem is very hard, it is very interesting to solve it for the important particular case of knotted tori. Recent classification results for knotted tori [Skopenkov2006a], [Cencelj&Repovš&Skopenkov2007], [Cencelj&Repovš&Skopenkov2008],
[Skopenkov2015], [Skopenkov2015a] give some insight or even precise information concerning arbitrary manifolds (cf. [Skopenkov2007], [Skopenkov2010], [Skopenkov2014]) and reveals new interesting relations to algebraic topology.
, i.e. knotted tori. See Hudson tori, [Alexander1924], [Milgram&Rees1971], [Kosinski1961], [Hudson1963], [Wall1965], [Tindell1969], [Boechat&Haefliger1970], [Boechat1971], [Milgram&Rees1971], [Lucas&Saeki2002], [Skopenkov2002]. A classification of knotted tori is a natural next step (after the link theory [Haefliger1966a] and the classification of embeddings of highly-connected manifolds) towards classification of embeddings of arbitrary manifolds. Since the general Knotting Problem is very hard, it is very interesting to solve it for the important particular case of knotted tori. Recent classification results for knotted tori [Skopenkov2006a], [Cencelj&Repovš&Skopenkov2007], [Cencelj&Repovš&Skopenkov2008],
[Skopenkov2015], [Skopenkov2015a] give some insight or even precise information concerning arbitrary manifolds (cf. [Skopenkov2007], [Skopenkov2010], [Skopenkov2014]) and reveals new interesting relations to algebraic topology.
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3]. Denote
3]. Denote
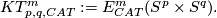
2 Examples
One of the first examples were Hudson tori.
Let us construct a map
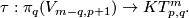
Recall that 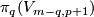 is isomorphic to the group of smooth maps
is isomorphic to the group of smooth maps 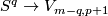 up to smooth homotopy. The latter maps can be considered as smooth maps
up to smooth homotopy. The latter maps can be considered as smooth maps 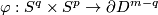 . Define the smooth embedding
. Define the smooth embedding 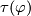 as the composition
as the composition
Tex syntax error
Tex syntax erroris the projection onto the second factor and
 is the standard inclusion.
is the standard inclusion.
See construction of another map in [Skopenkov2015,  3, definition of
3, definition of 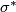 ].
].
An 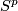 -parametric connected sum group structure on
-parametric connected sum group structure on 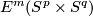 is constructed for
is constructed for 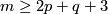 in [Skopenkov2006], [Skopenkov2015a].
in [Skopenkov2006], [Skopenkov2015a].
3 Classification
From the Haefliger-Zeeman Isotopy Theorem it follows that 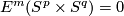 for
for 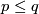 and
and 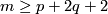 , provided that
, provided that 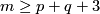 or
or 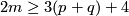 in the PL or smooth category, respectively. The dimension restriction in this result is sharp by the example of Hudson tori.
in the PL or smooth category, respectively. The dimension restriction in this result is sharp by the example of Hudson tori.
Theorem 3.1. There are 1-1 correspondences
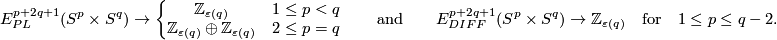
This result can be generalized as follows.
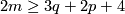 and
and 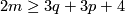 , in the PL and DIFF categories respectively, then there is a 1-1 correspondence
, in the PL and DIFF categories respectively, then there is a 1-1 correspondence 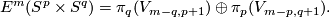
This follows for 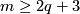 from the Becker-Glover Theorem 5.3. For the general case see [Skopenkov2002, Corollary 1.5.a]. For
from the Becker-Glover Theorem 5.3. For the general case see [Skopenkov2002, Corollary 1.5.a]. For 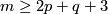 there is an alternative direct proof [Skopenkov2006], [Skopenkov2015a], but for
there is an alternative direct proof [Skopenkov2006], [Skopenkov2015a], but for 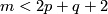 no proof of Theorem 3.2 without referring to `the deleted product method' is known.
no proof of Theorem 3.2 without referring to `the deleted product method' is known.
For 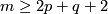 (which is automatic for
(which is automatic for 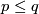 and
and 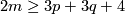 ) we have
) we have 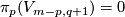 and the 1-1 correspondence of Theorem 3.2 is
and the 1-1 correspondence of Theorem 3.2 is  .
.
4 References
- [Alexander1924] J. W. Alexander, On the subdivision of 3-space by polyhedron, Proc. Nat. Acad. Sci. USA, 10, (1924) 6–8. Zbl 50.0659.01
- [Boechat&Haefliger1970] J. Boéchat and A. Haefliger, Plongements différentiables des variétés orientées de dimension
 dans
dans 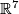 , (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
, (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
- [Boechat1971] J. Boéchat, Plongements de variétées différentiables orientées de dimension
 dans
dans 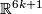 , Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
, Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
- [Cencelj&Repovš&Skopenkov2007] M. Cencelj, D. Repovš and M. Skopenkov, Homotopy type of the complement of an immersion and classification of embeddings of tori., Russ. Math. Surv.62 (2007), no.5, 985-987. Zbl 1141.57009
- [Cencelj&Repovš&Skopenkov2008] M. Cencelj, D. Repovš and M. Skopenkov, Classification of knotted tori in the 2-metastable dimension, Mat. Sbornik, 203:11 (2012), 1654-1681. Available at the arXiv:0811.2745.
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Hudson1963] J. F. P. Hudson, Knotted tori, Topology 2 (1963), 11–22. MR0146829 (26 #4349) Zbl 0151.32503
- [Kosinski1961] A. Kosinski, On Alexander's theorem and knotted tori, In: Topology of 3-Manifolds, Prentice-Hall, Englewood Cliffs, Ed. M.~K.~Fort, N.J., 1962, 55--57. Cf. Fort1962.
- [Lucas&Saeki2002] L. A. Lucas and O. Saeki, Embeddings of
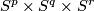 in
in 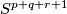 , Pacific J. Math. 207 (2002), no.2, 447–462. MR1972255 (2004c:57045) Zbl 1058.57022
, Pacific J. Math. 207 (2002), no.2, 447–462. MR1972255 (2004c:57045) Zbl 1058.57022
- [Milgram&Rees1971] R. Milgram and E. Rees, On the normal bundle to an embedding., Topology 10 (1971), 299-308. MR0290391 (44 #7572) Zbl 0207.22302
- [Skopenkov2002] A. Skopenkov, On the Haefliger-Hirsch-Wu invariants for embeddings and immersions., Comment. Math. Helv. 77 (2002), no.1, 78-124. MRMR1898394 (2003c:57023) Zbl 1012.57035
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2006a] A. Skopenkov, Classification of embeddings below the metastable dimension. Available at the arXiv:0607422.
- [Skopenkov2007] A. Skopenkov, A new invariant and parametric connected sum of embeddings, Fund. Math. 197 (2007), 253–269. arXiv:math/0509621. MR2365891 (2008k:57044) Zbl 1145.57019
- [Skopenkov2010] A. Skopenkov, Embeddings of k-connected n-manifolds into
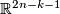 , Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
, Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
- [Skopenkov2014] A. Skopenkov, How do autodiffeomorphisms act on embeddings, Proc. A of the Royal Society of Edinburgh, 148:4 (2018) 835--848.
- [Skopenkov2015] M. Skopenkov, When is the set of embeddings finite up to isotopy? Intern. J. Math. 26:7 (2015), http://arxiv.org/abs/1106.1878
- [Skopenkov2015a] A. Skopenkov, A classification of knotted tori, Proc. A of the Royal Society of Edinburgh, 150:2 (2020), 549-567. Full version: http://arxiv.org/abs/1502.04470
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Tindell1969] R. Tindell, Extending homeomorphisms of
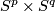 ., Proc. Am. Math. Soc. 22 (1969), 230-232. MRMR0248852 (40 #2102) Zbl 0177.26802
., Proc. Am. Math. Soc. 22 (1969), 230-232. MRMR0248852 (40 #2102) Zbl 0177.26802
- [Wall1965] C. T. C. Wall, Unknotting tori in codimension one and spheres in codimension two., Proc. Camb. Philos. Soc. 61 (1965), 659-664. MR0184249 (32 #1722) Zbl 0135.41602
This result can be generalized as follows. {{beginthm|Theorem}}\label{kt} If m\ge3q+2p+4$ and m\ge3q+3p+4$, in the PL and DIFF categories respectively, then there is a 1-1 correspondence $$E^m(S^p\times S^q)=\pi_q(V_{m-q,p+1})\oplus\pi_p(V_{m-p,q+1}).$$ {{endthm}} This follows for $m\ge 2q+3$ from [[Embeddings_just_below_the_stable_range:_classification#Classification_further_below_the_stable_range|the Becker-Glover Theorem 5.3]]. For the general case see \cite[Corollary 1.5.a]{Skopenkov2002}. For $m\ge2p+q+3$ there is an alternative direct proof \cite{Skopenkov2006}, \cite{Skopenkov2015a}, but for $m<2p+q+2$ no proof of Theorem \ref{kt} without referring to `the deleted product method' is known. For $m\ge2p+q+2$ (which is automatic for $p\le q$ and m\ge3p+3q+4$) we have $\pi_p(V_{m-p,q+1})=0$ and the 1-1 correspondence of Theorem \ref{kt} is $\tau$.
For a general introduction to embeddings as well as the notation and conventions used on this page, we refer to [Skopenkov2016c,  1,
1,  3]. Denote
3]. Denote
2 Examples
One of the first examples were Hudson tori.
Let us construct a map
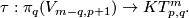
Recall that 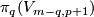 is isomorphic to the group of smooth maps
is isomorphic to the group of smooth maps 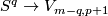 up to smooth homotopy. The latter maps can be considered as smooth maps
up to smooth homotopy. The latter maps can be considered as smooth maps 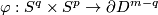 . Define the smooth embedding
. Define the smooth embedding 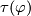 as the composition
as the composition
Tex syntax error
Tex syntax erroris the projection onto the second factor and
 is the standard inclusion.
is the standard inclusion.
See construction of another map in [Skopenkov2015,  3, definition of
3, definition of 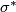 ].
].
An 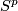 -parametric connected sum group structure on
-parametric connected sum group structure on 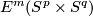 is constructed for
is constructed for 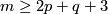 in [Skopenkov2006], [Skopenkov2015a].
in [Skopenkov2006], [Skopenkov2015a].
3 Classification
From the Haefliger-Zeeman Isotopy Theorem it follows that 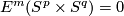 for
for 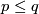 and
and 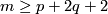 , provided that
, provided that 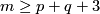 or
or 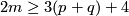 in the PL or smooth category, respectively. The dimension restriction in this result is sharp by the example of Hudson tori.
in the PL or smooth category, respectively. The dimension restriction in this result is sharp by the example of Hudson tori.
Theorem 3.1. There are 1-1 correspondences
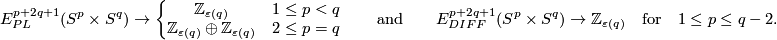
This result can be generalized as follows.
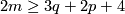 and
and 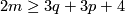 , in the PL and DIFF categories respectively, then there is a 1-1 correspondence
, in the PL and DIFF categories respectively, then there is a 1-1 correspondence 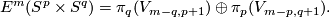
This follows for 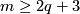 from the Becker-Glover Theorem 5.3. For the general case see [Skopenkov2002, Corollary 1.5.a]. For
from the Becker-Glover Theorem 5.3. For the general case see [Skopenkov2002, Corollary 1.5.a]. For 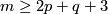 there is an alternative direct proof [Skopenkov2006], [Skopenkov2015a], but for
there is an alternative direct proof [Skopenkov2006], [Skopenkov2015a], but for 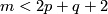 no proof of Theorem 3.2 without referring to `the deleted product method' is known.
no proof of Theorem 3.2 without referring to `the deleted product method' is known.
For 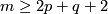 (which is automatic for
(which is automatic for 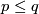 and
and 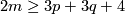 ) we have
) we have 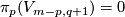 and the 1-1 correspondence of Theorem 3.2 is
and the 1-1 correspondence of Theorem 3.2 is  .
.
4 References
- [Alexander1924] J. W. Alexander, On the subdivision of 3-space by polyhedron, Proc. Nat. Acad. Sci. USA, 10, (1924) 6–8. Zbl 50.0659.01
- [Boechat&Haefliger1970] J. Boéchat and A. Haefliger, Plongements différentiables des variétés orientées de dimension
 dans
dans 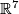 , (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
, (French) Essays on Topology and Related Topics (Mémoires dédiés à Georges de Rham), Springer, New York (1970), 156–166. MR0270384 (42 #5273) Zbl 0199.27003
- [Boechat1971] J. Boéchat, Plongements de variétées différentiables orientées de dimension
 dans
dans 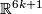 , Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
, Comment. Math. Helv. 46 (1971), 141–161. MR0295373 (45 #4439) Zbl 0218.57016
- [Cencelj&Repovš&Skopenkov2007] M. Cencelj, D. Repovš and M. Skopenkov, Homotopy type of the complement of an immersion and classification of embeddings of tori., Russ. Math. Surv.62 (2007), no.5, 985-987. Zbl 1141.57009
- [Cencelj&Repovš&Skopenkov2008] M. Cencelj, D. Repovš and M. Skopenkov, Classification of knotted tori in the 2-metastable dimension, Mat. Sbornik, 203:11 (2012), 1654-1681. Available at the arXiv:0811.2745.
- [Haefliger1966a] A. Haefliger, Enlacements de sphères en co-dimension supérieure à 2, Comment. Math. Helv.41 (1966), 51-72. MR0212818 (35 #3683) Zbl 0149.20801
- [Hudson1963] J. F. P. Hudson, Knotted tori, Topology 2 (1963), 11–22. MR0146829 (26 #4349) Zbl 0151.32503
- [Kosinski1961] A. Kosinski, On Alexander's theorem and knotted tori, In: Topology of 3-Manifolds, Prentice-Hall, Englewood Cliffs, Ed. M.~K.~Fort, N.J., 1962, 55--57. Cf. Fort1962.
- [Lucas&Saeki2002] L. A. Lucas and O. Saeki, Embeddings of
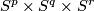 in
in 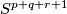 , Pacific J. Math. 207 (2002), no.2, 447–462. MR1972255 (2004c:57045) Zbl 1058.57022
, Pacific J. Math. 207 (2002), no.2, 447–462. MR1972255 (2004c:57045) Zbl 1058.57022
- [Milgram&Rees1971] R. Milgram and E. Rees, On the normal bundle to an embedding., Topology 10 (1971), 299-308. MR0290391 (44 #7572) Zbl 0207.22302
- [Skopenkov2002] A. Skopenkov, On the Haefliger-Hirsch-Wu invariants for embeddings and immersions., Comment. Math. Helv. 77 (2002), no.1, 78-124. MRMR1898394 (2003c:57023) Zbl 1012.57035
- [Skopenkov2006] A. Skopenkov, Embedding and knotting of manifolds in Euclidean spaces, in: Surveys in Contemporary Mathematics, Ed. N. Young and Y. Choi, London Math. Soc. Lect. Notes, 347 (2008) 248-342. Available at the arXiv:0604045.
- [Skopenkov2006a] A. Skopenkov, Classification of embeddings below the metastable dimension. Available at the arXiv:0607422.
- [Skopenkov2007] A. Skopenkov, A new invariant and parametric connected sum of embeddings, Fund. Math. 197 (2007), 253–269. arXiv:math/0509621. MR2365891 (2008k:57044) Zbl 1145.57019
- [Skopenkov2010] A. Skopenkov, Embeddings of k-connected n-manifolds into
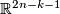 , Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
, Proc. AMS, 138 (2010) 3377--3389. Available at the arXiv:0812.0263.
- [Skopenkov2014] A. Skopenkov, How do autodiffeomorphisms act on embeddings, Proc. A of the Royal Society of Edinburgh, 148:4 (2018) 835--848.
- [Skopenkov2015] M. Skopenkov, When is the set of embeddings finite up to isotopy? Intern. J. Math. 26:7 (2015), http://arxiv.org/abs/1106.1878
- [Skopenkov2015a] A. Skopenkov, A classification of knotted tori, Proc. A of the Royal Society of Edinburgh, 150:2 (2020), 549-567. Full version: http://arxiv.org/abs/1502.04470
- [Skopenkov2016c] A. Skopenkov, Embeddings in Euclidean space: an introduction to their classification, to appear to Bull. Man. Atl.
- [Tindell1969] R. Tindell, Extending homeomorphisms of
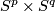 ., Proc. Am. Math. Soc. 22 (1969), 230-232. MRMR0248852 (40 #2102) Zbl 0177.26802
., Proc. Am. Math. Soc. 22 (1969), 230-232. MRMR0248852 (40 #2102) Zbl 0177.26802
- [Wall1965] C. T. C. Wall, Unknotting tori in codimension one and spheres in codimension two., Proc. Camb. Philos. Soc. 61 (1965), 659-664. MR0184249 (32 #1722) Zbl 0135.41602