Talk:Fibre homotopy trivial bundles (Ex)
We consider 5-dimensional real vector bundles over 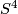 .
Isomorphism classes of these are given by their clutching function in
.
Isomorphism classes of these are given by their clutching function in 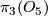 .
.
Given that 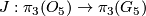 is isomorphic to the surjection
is isomorphic to the surjection 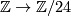 ,
we see that the vector bundle
,
we see that the vector bundle 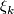 corresponding to
corresponding to 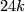 times the generator
has a sphere bundle
times the generator
has a sphere bundle 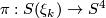 which is fiber homotopically trivial, so in particular we have
homotopy equivalences
which is fiber homotopically trivial, so in particular we have
homotopy equivalences 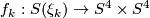 .
.
From another exercise we know that stably 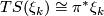 .
From a third exercise we know that the first Pontryagin class of
.
From a third exercise we know that the first Pontryagin class of 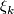 is
is 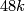 times the generator of
times the generator of 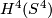 .
.
It follows that the first Pontryagin class of 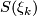 is non-trivial, since under
is non-trivial, since under 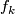 the map
the map 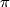 just corresponds to projection to one factor.
Hence
just corresponds to projection to one factor.
Hence 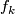 is a homotopy equivalence which doesn't preserve the first Pontryagin class, as
is a homotopy equivalence which doesn't preserve the first Pontryagin class, as 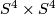 has
stably trivial tangent bundle, hence trivial
has
stably trivial tangent bundle, hence trivial 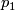 .
.
Similarly one can argue with 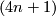 -dimensional vector bundles over
-dimensional vector bundles over 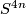 ; the
; the 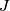 -homomorphism has always
a non-trivial kernel, and the top Pontryagin class of the corresponding bundles are non-zero. This produces
homotopy equivalences
-homomorphism has always
a non-trivial kernel, and the top Pontryagin class of the corresponding bundles are non-zero. This produces
homotopy equivalences 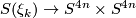 which do not preserve
which do not preserve 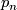 .
.