Tangent bundles of bundles (Ex)
From Manifold Atlas
Let 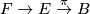 be a smooth fiber bundle so that all spaces
be a smooth fiber bundle so that all spaces 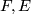 and
and  are manifolds.
are manifolds.
Exercise 0.1.
Show that 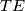 , the tangent bundle of
, the tangent bundle of  , splits as the sum of two bundles
, splits as the sum of two bundles
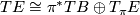
where 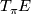 consists of those tangent vectors tangent to the fibres of
consists of those tangent vectors tangent to the fibres of  .
.
Question 0.2.
Is the bundle 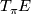 the pullback of some bundle over
the pullback of some bundle over  ?
?
Exercise 0.3.
Suppose that 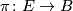 is itself a smooth vector bundle. Determine
is itself a smooth vector bundle. Determine 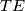 in terms of
in terms of 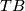 and
and  regarded as a vector bundle.
regarded as a vector bundle.
Exercise 0.4.
Suppose that 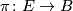 is the sphere bundle of a vector bundle. Determine the stable tangent bundle of
is the sphere bundle of a vector bundle. Determine the stable tangent bundle of  in terms of
in terms of  and
and 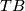 .
.
As an explicit example, recall that there are principal bundles 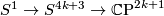 and
and 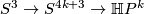 . It follows that there is an
. It follows that there is an  fibre bundle
fibre bundle 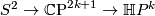 with structure group
with structure group  acting on
acting on  via
via 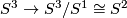 .
.
Exercise 0.5. Compute the total Pontrjagin class of 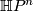 , quaternionic projective space. (This was first achieved in [Hirzebruch1953]).
, quaternionic projective space. (This was first achieved in [Hirzebruch1953]).
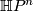 , quaternionic projective space. (This was first achieved in [Hirzebruch1953]).
, quaternionic projective space. (This was first achieved in [Hirzebruch1953]).