Fibre homotopy trivial bundles (Ex)
From Manifold Atlas
Exercise 0.1.
- Observe that
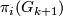 classifies
classifies  -spherical fibrations over
-spherical fibrations over 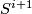 . Using the isomorphisms
. Using the isomorphisms 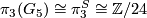 ,
, 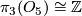 and the fact that the J-homomophism in dimension
and the fact that the J-homomophism in dimension  is isomorphic to the surjective homomorphism
is isomorphic to the surjective homomorphism 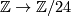 , find a homotopy equivalence of manifolds
, find a homotopy equivalence of manifolds 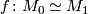 such that
such that 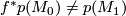 . Here
. Here 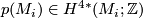 denotes the total Pontrjagin class.
denotes the total Pontrjagin class.
- The above exercise showed that the first Pontrjain class,
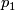 , is not a homotopy invariant. Apply the same idea to show that
, is not a homotopy invariant. Apply the same idea to show that 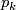 is not a homotopy invariant for any
is not a homotopy invariant for any 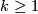 .
.
Remark 0.2. A reference to Novikov is needed here.