Milnor Hypersurfaces
From Manifold Atlas
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
[edit] 1 Introduction
The Milnor hypersurfaces, denoted 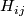 , are a family of smooth manifolds that generate (with redundancy) the complex bordism ring.
, are a family of smooth manifolds that generate (with redundancy) the complex bordism ring.
[edit] 2 Construction and examples
For fixed natural numbers 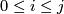 ,
, 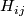 is defined as the hypersurface in
is defined as the hypersurface in 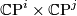 satisfying the equation
satisfying the equation 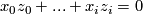 , where
, where 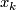 and
and 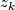 are homogeneous coordinates for
are homogeneous coordinates for 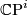 and
and 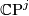 respectively.
This equation defines a generic hyperplane intersecting the image of the Segre embedding
respectively.
This equation defines a generic hyperplane intersecting the image of the Segre embedding 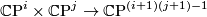 transversely.
transversely.
The role of these manifolds in complex bordism is described on the page Complex bordism.
[edit] 3 Invariants
The signature of the Milnor hypersurfaces is known: