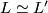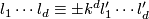Lens spaces
|
This page has not been refereed. The information given here might be incomplete or provisional. |
Contents |
[edit] 1 Introduction
A lens space is the orbit spaces of a free linear action of a finite cyclic group on a sphere. The importance of lens spaces stems from the fact that they provide examples of peculiar phenomena. For example, there are pairs of lens spaces where both lens spaces have the same homotopy and homology groups but are not homotopy equivalent, and there are also pairs where both lens spaces are homotopy equivalent, but not homeomorphic. The lens spaces also play a role in Milnor's disproof of Hauptvermutung for polyhedra, that means they were used to find two polyhedra which are homeomorphic but combinatorially distinct.
For historical information about 3-dimensional lens spaces, see Lens spaces in dimension three: a history.
For information about manifold homotopy equivalent to lens spaces, see the page on fake lens spaces.
[edit] 2 Construction and examples
Let  ,
, 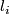 for
for 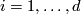 be natural numbers such that
be natural numbers such that 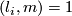 for all
for all  . The lens space
. The lens space 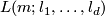 is defined to be the orbit space of the free action of the cyclic group
is defined to be the orbit space of the free action of the cyclic group 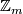 on the sphere
on the sphere 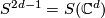 given by the formula
given by the formula
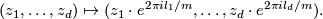
[edit] 3 Invariants
Abbreviate 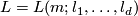 .
.
-
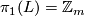 ,
, 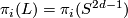 for
for 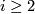
-
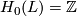 ,
, 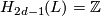 ,
, 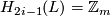 for
for 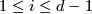 ,
, 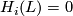 for all other values of
for all other values of  .
.
- Let
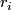 be natural numbers satisfying
be natural numbers satisfying 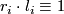 mod
mod  for all
for all  . Then the Reidemeister torsion is given by
. Then the Reidemeister torsion is given by
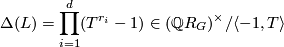
where ![\Qq R_G = \Qq [T] / (1+T+\cdots + T^{m-1})](/images/math/4/4/7/44765754ba359ae7d0edcd0d7f0d7e6f.png) (see p406 of [Milnor1966]).
(see p406 of [Milnor1966]).
- Let
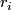 be natural numbers satisfying
be natural numbers satisfying 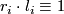 mod
mod  for all
for all  . Then the Rho-invariant is defined by (p187 of [Wall1999])
. Then the Rho-invariant is defined by (p187 of [Wall1999])
![\displaystyle \rho (L) = \prod_{i=1}^{d}\frac{(\chi^{r_i} +1)}{(\chi^{r_i}-1)} \in \Qq R_{\widehat G} = \Qq [\chi] / \langle 1 + \chi + \cdots + \chi^{N-1} \rangle.](/images/math/9/2/b/92b517d27913ecc104c7bb9c7cfb92db.png)
For the notation in the last two points click here
[edit] 4 Classification/Characterization
Abbreviate 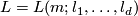 and
and 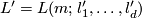 .
.
[edit] 1 Homotopy classification
See also [Cohen1973].
[edit] 2 PL homeomorphism classification
Theorem 4.2 [Franz1935],[De Rham1936]. 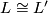 if and only if for some permutation
if and only if for some permutation 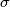 and some
and some 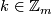 we have
we have 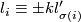 for all
for all  .
.
[edit] 3 Homeomorphism classification
Theorem 4.3 [Brody1960a]. 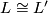 if and only if for some permutation
if and only if for some permutation 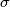 and some
and some 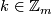 we have
we have 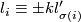 for all
for all  .
.
See also [Milnor1966]
[edit] 4  -cobordism classification
-cobordism classification
Theorem 4.4 [Atiyah&Bott1968]. Two lens spaces  ,
, 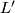 are
are  -cobordant if and only if they are homeomorphic.
-cobordant if and only if they are homeomorphic.
See also [Milnor1966]
[edit] 5 Further discussion
More details and a discussion of fake lens spaces are planned. This includes the  -invariant.
-invariant.
[edit] 6 References
- [Atiyah&Bott1968] M. F. Atiyah and R. Bott, A Lefschetz fixed point formula for elliptic complexes. II. Applications, Ann. of Math. (2) 88 (1968), 451–491. MR0232406 (38 #731) Zbl 0167.21703
- [Brody1960a] E. J. Brody, The topological classification of the lens spaces, Ann. of Math. (2) 71 (1960), 163–184. MR0116336 (22 #7125) Zbl 0119.18901
- [Cohen1973] M. M. Cohen, A course in simple-homotopy theory, Springer-Verlag, New York, 1973. MR0362320 (50 #14762) Zbl 0261.57009
- [De Rham1936] G. de Rham, Sur les nouveaux invariants topologiques de M. Reidemeister, Rec. Math. [Mat. Sbornik], Moscou, Volume 1(43), (1936), 737-742. Zbl 0016.04501
- [Franz1935] W. Franz, Über die Torsion einer Überdeckung., Journ. f. Math. 173 (1935), 245-254. Zbl 61.1350.01
- [Milnor1966] J. Milnor, Whitehead torsion, Bull. Amer. Math. Soc. 72 (1966), 358–426. MR0196736 (33 #4922) Zbl 0147.23104
- [Olum1953] P. Olum, Mappings of manifolds and the notion of degree, Ann. of Math. (2) 58 (1953), 458–480. MR0058212 (15,338a) Zbl 0052.19901
- [Wall1999] C. T. C. Wall, Surgery on compact manifolds, American Mathematical Society, Providence, RI, 1999. MR1687388 (2000a:57089) Zbl 0935.57003
[edit] 7 External links
- The Wikipedia page about lens spaces.