Lens spaces in dimension three: a history
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 09:23, 13 May 2013 and the changes since publication. |
|
The user responsible for this page is Klaus Volkert. No other user may edit this page at present. |
Lens spaces are a particular class of closed orientable 3-manifolds which played an important role in the history of manifolds; they were obtained by identifications on a 2-sphere bounding a 3-ball or by Heegard's method using tori. The Heegard splitting is of genus one, that is the reason why lens spaces are rather simple 3-manifolds.
The first mathematician who mentioned lens spaces - this name wasn't introduced until 1931 (cf. below) - was W. Dyck. He did this in a talk delivered to the British Association for the Advancement of Science held in Montreal 1884 ([Dyck1885]). After describing the construction of 3-manifolds by identifying homeomorphic surfaces of handle bodies - today known as Heegard diagrams - in a rather general way, Dyck gave two examples. Take two solid tori and define the identifications of their surfaces by fixing the images of the meridians and the latitudinal curves of the first torus on the other. Two possibilities occur:
``First, ..., we can make them correspond such that meridian curves fall on meridian curves, and latitudinal curves into latitudinal curves.´´ ([Dyck1885, 648])
The other possibility is to map meridians to latitudinal curves and vice versa. Dyck observed that in the first case they are closed curves in the resulting 3-manifold which are not null-homotopic whereas such curves don't exist in the second case. In modern notation, Dyck's first example is the lens space 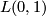 (the product
(the product 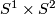 ), the second is nothing but
), the second is nothing but  . Dyck didn't publish more about his ideas; he gave them up in favour of a more combinatorial approach on which he published two more papers ([Dyck1888],[Dyck1890]) before leaving topology completely. The history of the 3-sphere and of projective space which both can be considered as lens spaces are discussed in separate articles. Therefore they are not considered further here.
. Dyck didn't publish more about his ideas; he gave them up in favour of a more combinatorial approach on which he published two more papers ([Dyck1888],[Dyck1890]) before leaving topology completely. The history of the 3-sphere and of projective space which both can be considered as lens spaces are discussed in separate articles. Therefore they are not considered further here.
In 1908, H. Tietze discussed lens spaces in length; their importance lay in the fact that they are rather simple: ``ein in gewisser Hinsicht möglichst einfacher Typus von zweiseitigen geschlossenen dreidimensionalen Mannigfaltigkeiten´´ [1]; ([Tietze1908, 110]). The space 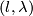 (we will use the modern symbol
(we will use the modern symbol 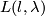 for it) is defined as follows: Take a 3-ball bounded by a 2-sphere. The equator of this sphere is divided into
for it) is defined as follows: Take a 3-ball bounded by a 2-sphere. The equator of this sphere is divided into  equal parts. Let
equal parts. Let 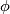 denote the length of the points on the upper half-sphere,
denote the length of the points on the upper half-sphere, 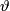 their latitude;
their latitude; 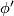 and
and 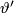 denote the same quantities on the lower half-sphere. Then the identification is given by
denote the same quantities on the lower half-sphere. Then the identification is given by
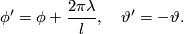
So the identification is made by rotating the upper halfsphere by the angle 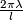 and then identifying points on the same meridian which are equidistant to the equator. Obivously the rotation by
and then identifying points on the same meridian which are equidistant to the equator. Obivously the rotation by  yields the projective space; in this case
yields the projective space; in this case 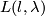 is
is 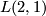 . The only interesting cases are those in which
. The only interesting cases are those in which  and
and  have no common divisor.
have no common divisor.
Using the decomposition in cells defined by this identification Tietze was able to calculate the fundamental group of the lens space 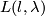 : it is the cyclic group with
: it is the cyclic group with  elements, in particular it does not dependend on
elements, in particular it does not dependend on  . The first Betti number is zero but there is a torsion coefficient equal to l. By duality the second Betti number of the lens spaces can be calculated.
. The first Betti number is zero but there is a torsion coefficient equal to l. By duality the second Betti number of the lens spaces can be calculated.
Tietze remarked that lens spaces can also be constructed by identifying the surfaces of two solid tori (as Dyck did it) and as branched covers of  (with ramification points). This idea is attributed to W. Wirtinger, his teacher; traces of it can be found in Heegard's dissertation (1898)([Epple1999], Chapter 8.2, Chapter 8.3).
(with ramification points). This idea is attributed to W. Wirtinger, his teacher; traces of it can be found in Heegard's dissertation (1898)([Epple1999], Chapter 8.2, Chapter 8.3).
Like Poincaré, Tietze was interested in classifying 3-manifolds. He asked himself the question whether the known invariants (the fundamental group, the Betti numbers, the torsion coefficients) suffice to determine such a manifold up to homeomorphism. He conjectured a negative answer after analyzing the structure of the two lens spaces 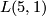 and
and 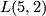 :
:
``Die eben angestellte Betrachtung der Mannigfaltigkeiten [5,1] und [5,2], die beide die zyklische Gruppe 5. Ordnung zur Fundamentalgruppe haben, zeigt, daß gewisse Anordnungsverhältnisse der Schemata auch in der Fundamentalgruppe nicht zum Ausdruck kommen.´´ [2] ([Tietze1908, 117sq])
This conjecture was proven by J. W. Alexander in [Alexander1919]. Alexander used Heegard's diagrams to get the lens space; during a stay in Paris he was assigned the task to check the details of the French translation of Heegaard's dissertation. Alexander wrote:
``It is proposed to set up an example of two 3-dimensional manifolds which are by no means equivalent but which cannot even be differentiated by their groups.´´ ([Alexander1919, 339])
By a difficult analysis of the geometric situation concerning 1-cycles, Alexander derived the result he needed (for more details c.f. [Stillwell1993, 258-260]). This approach was systematized by Alexander himself some years later, the result was the theory of `Eigenverschlingungszahlen ([Alexander1924a]) which was refined by H. Seifert ([Seifert1933]). But even these invariants were not able to distinguish 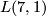 and
and 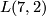 . The classification of lens spaces became an important question which wasn't answered until the 1930s in the work of Seifert and Threlfall and in the work of Reidemeister and Franz. In particular the idea of the lens shape will appear only in the paper [Threlfall&Seifert1931].
. The classification of lens spaces became an important question which wasn't answered until the 1930s in the work of Seifert and Threlfall and in the work of Reidemeister and Franz. In particular the idea of the lens shape will appear only in the paper [Threlfall&Seifert1931].
In their first joint paper ([Threlfall&Seifert1931]) Seifert and Threlfall studied only a special type of lens space, today noted by 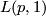 . Those spaces were obtained as orbit spaces using the operation of a finite cyclic subgroup of SO(4) of order
. Those spaces were obtained as orbit spaces using the operation of a finite cyclic subgroup of SO(4) of order  on
on  ([Volkert2002], [Volkert2005]). The fundamental domain of that subgroup is the intersection of certain balls - their boundaries are symmetry planes in the sense of spherical geometry - which all pass through a circle. Threlfall and Seifert explain the situation in Figure 1.
([Volkert2002], [Volkert2005]). The fundamental domain of that subgroup is the intersection of certain balls - their boundaries are symmetry planes in the sense of spherical geometry - which all pass through a circle. Threlfall and Seifert explain the situation in Figure 1.
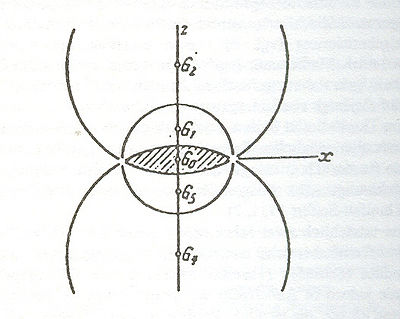
The acute edge of the lens is nothing but the circle through which all spheres pass. It is subdivided in  equal parts, the identification of the lower and the upper half of the lens is provided by a screw motion. In their second joint work ([Threlfall&Seifert1933]) the authors also gave an interpretation of the general lens spaces
equal parts, the identification of the lower and the upper half of the lens is provided by a screw motion. In their second joint work ([Threlfall&Seifert1933]) the authors also gave an interpretation of the general lens spaces 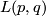 by reducing the question about the finite subgroups of SO(4) to that of finite subgroups of SO(3) using the epimorphism
by reducing the question about the finite subgroups of SO(4) to that of finite subgroups of SO(3) using the epimorphism
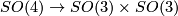
due to [Goursat1889].
In their second paper Threlfall and Seifert also proved a theorem which is a partial solution to the classification problem of lens spaces: The lens spaces 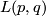 and
and 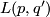 are not homeomorphic if
are not homeomorphic if 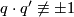 mod
mod  . If they are homeomorphic then
. If they are homeomorphic then 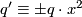 mod
mod  has a solution ([Threlfall&Seifert1933, 551]).
has a solution ([Threlfall&Seifert1933, 551]).
The classification problem for lens spaces was completely solved by K. Reidemeister, who proved that the sufficient condition given by Seifert and Threlfall is also necessary ([Reidemeister1935a]); actually Reidemeister worked in the combinatorial frame, in order to extend his result to homeommorphy the answer to the Hauptvermutung was necessary. The method used by Reidemeister ([Reidemeister1935]) was generalized by W. Franz ([Franz1935]) by introducing the now so-called Reidemister-Franz torsion.
J.H.C. Whitehead solved in 1941 the classification problem for lens spaces up to homotopy equivalence: Two lens spaces 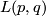 and
and 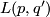 are homotopy equivalent if and only if there is a natural number
are homotopy equivalent if and only if there is a natural number  such that
such that 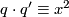 mod
mod  ([Whitehead1941]).
([Whitehead1941]).
1 Footnotes
- ↑ Translation: ``from a certain point of view, the simplest possible type of two-sided three-dimensional closed manifolds´´
- ↑ Translation:``The previous description of the manifolds [5, 1] and [5, 2], which both have fundamental group the cyclic group of order 5, shows that certain structural relations in the construction of these spaces are not visible in the fundamental group.´´
2 References
- [Alexander1919] J. W. Alexander, Note on two three dimensional manifolds with the same group, Trans. Amer. Math. Soc. 20 (1919), 339-342. MR1501131 Zbl 47.0964.01
- [Alexander1924a] J. W. Alexander, New topological invariants expressible as tensors., Nat. Acad. Proc. 10 (1924), 99-101. Zbl 50.0659.02
- [Dyck1885] W. Dyck, On the ``Analysis situs´´ of three-dimensional spaces, In: Report of the fifty-fourth Meeting of the British Association for the Advancement of Science, held at Montreal in August and September 1884 (London, 1885), 648.
- [Dyck1888] W. Dyck, Beiträge zur Analysis situs. I, Math. Ann. 37 (1888), no.2, 457–512. MR1510647 Zbl 20.0519.04
- [Dyck1890] W. Dyck, Beiträge zur Analysis situs. II, Math. Ann. 37 (1890) no.2, 273–316. MR510647 Zbl 22.0547.02
- [Epple1999] M. Epple, Die Entstehung der Knotentheorie, Braunschweig/Wiesbaden, (1999).
- [Franz1935] W. Franz, Über die Torsion einer Überdeckung., Journ. f. Math. 173 (1935), 245-254. Zbl 61.1350.01
- [Goursat1889] E. Goursat, Sur les substitutions orthogonales et les divisions régulières de l'espace, Ann. Sci. École. Norm. Sup. (3) 6 (1889), 9–102. MR1508819 Zbl 21.0673.03
- [Reidemeister1935] K. Reidemeister, Überdeckungen von Komplexen, J. Reine Angew. Math. 173 (1935), 164-173. MR1581465Zbl 0012.12604
- [Reidemeister1935a] K. Reidemeister, Homotopieringe und Linsenräume, Abh. Math. Semin. Hamb. Univ. 11 (1935), 102-109. MR3069647Zbl 0011.32404
- [Seifert1933] H. Seifert, Verschlingungsinvarianten, Sitzungsber. Preuß. Akad. Wiss., Phys.-Math. Kl. 1933, No.26-29, (1933) 811-828. Zbl 0008.18101
- [Stillwell1993] J. Stillwell, Classical topology and combinatorial group theory, Springer-Verlag, New York, 1993. MR1211642 (94a:57001) Zbl 0774.57002
- [Threlfall&Seifert1931] W. Threlfall and H. Seifert, Topologische Untersuchung der Diskontinuitätsbereiche endlicher Bewegungsgruppen des dreidimensionalen sphärischen Raumes, Math. Ann. 104 (1931), no.1, 1–70. MR1512649 Zbl 0006.03403
- [Threlfall&Seifert1933] W. Threlfall and H. Seifert, Topologische Untersuchung der Diskontinuitätsbereiche endlicher Bewegungsgruppen des dreidimensionalen sphärischen Raumes (Schluß), Math. Ann. 107 (1933), no.1, 543–586. MR1512817 Zbl 58.1203.01
- [Tietze1908] H. Tietze, Über die topologischen Invarianten mehrdimensionaler Mannigfaltigkeiten, Monatsh. Math. Phys. 19 (1908), no.1, 1–118. MR1547755 Zbl 39.0720.05
- [Volkert2002] K. Volkert, Das Homöomorphieproblem insbesondere der 3-Mannigfaltigkeiten, in der Topologie 1892 - 1935, Paris, 2002.
- [Volkert2005] K. Volkert, Le retour de la géométrie, in Géométrie au XXe siècle, ed. by J. Kouneiher, D. Flament, P. Nabonnand and J. Szczeciniarz (Paris, 2005), 150–162.
- [Whitehead1941] J. H. C. Whitehead, On incidence matrices, nuclei and homotopy types, Ann. of Math. (2) 42 (1941), 1197–1239. MR0005352 (3,142b) Zbl 0063.08227
3 External links
- The Wikipedia page about Lens spaces.