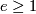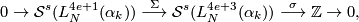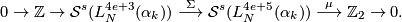Fake lens spaces
|
An earlier version of this page was published in the Bulletin of the Manifold Atlas: screen, print. You may view the version used for publication as of 15:18, 25 April 2013 and the changes since publication. |
|
The user responsible for this page is Tibor Macko. No other user may edit this page at present. |
Contents |
1 Introduction
A fake lens space is the orbit space of a free action of a finite cyclic group on a sphere. As such it is a topological manifold. If the action is required to be smooth then a smooth fake lens space is obtained. On this page mostly topological fake lens spaces are discussed, since for these the classification is better understood.
Clearly, classical lens spaces, which are orbit spaces of free actions on a sphere coming from unitary representations of a finite cyclic group, are examples of fake lens spaces. In order to obtain fake lens spaces which are not homeomorphic to these classical lens spaces more sophisticated technology is needed. One can either use surgery theoretic methods, or one can define certain actions of finite cyclic groups on Brieskorn varieties. See the constructions and examples below.
The classification of topological fake lens spaces can be seen as one of the basic questions in the topology of manifolds. It is systematically obtained in three stages: the homotopy classification using classical homotopy theory, the simple homotopy classification using Reidemeister torsion, and finally, surgery theory is employed to obtain a homeomorphism classification within the respective simple homotopy types. The classification of lens spaces with fundamental groups of order  with
with  odd and
odd and  , was one of the first spectacular applications of surgery theory (see [Browder1970], [Browder&Petrie&Wall1971], and the full classification in this setting in [Wall1999, chapters 14D, 14E]).
, was one of the first spectacular applications of surgery theory (see [Browder1970], [Browder&Petrie&Wall1971], and the full classification in this setting in [Wall1999, chapters 14D, 14E]).
2 Definition
Definition 2.1.
Let  be a finite cyclic group and let
be a finite cyclic group and let  be a free action of
be a free action of  by homeomorphisms on the sphere
by homeomorphisms on the sphere 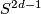 . A fake lens space is the orbit space of
. A fake lens space is the orbit space of  and it is denoted by
and it is denoted by 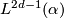 .
.
Recall that the classical lens spaces were denoted by symbols like 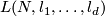 , where
, where  is the order of the group
is the order of the group  . For brevity the notation
. For brevity the notation 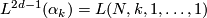 is sometimes used below. Also, when the dimension and the action are clear, we sometimes leave them from notation and simply write
is sometimes used below. Also, when the dimension and the action are clear, we sometimes leave them from notation and simply write  .
.
Note that by the Lefschetz fixed point theorem, only the group of order 2 can act freely on a sphere 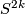 of even dimension. For this case see the article on fake real projective spaces.
of even dimension. For this case see the article on fake real projective spaces.
3 Notation
Throughout this page  will be the finite cyclic group of order
will be the finite cyclic group of order  . It will have a preferred generator
. It will have a preferred generator  which allows us to identify
which allows us to identify
![\displaystyle \Zz G = \Zz [T] / \langle T^N -1 \rangle.](/images/math/8/d/a/8dad73539afa5eb82ddf66d16deb710c.png)
The norm element is 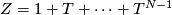 . Further we denote
. Further we denote ![R_G = \Zz G / \langle Z \rangle = \Zz [T]/ \langle 1 + T + \cdots + T^{N-1} \rangle](/images/math/7/9/d/79d1d3912b2e7ce3ff3135f81c7d634c.png) . The projection map
. The projection map 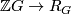 fits into the arithmetic square:
fits into the arithmetic square:
![\displaystyle \xymatrix{ \Zz G \ar[r]^{\eta} \ar[d]_{\varepsilon} & R_G \ar[d]^{\varepsilon'} \\ \Zz \ar[r]_{\eta'} & \Zz_N }](/images/math/3/4/d/34da3249bf4eb2eac0505f1c05c1a32f.png)
where  ,
, 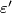 are the augmentation maps. The augmentation ideal is the kernel
are the augmentation maps. The augmentation ideal is the kernel 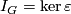 .
.
We will also need the ring 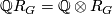 which we identify as
which we identify as
![\displaystyle \Qq R_G = \Qq [T]/ \langle 1 + T + \cdots + T^{N-1} \rangle.](/images/math/a/d/f/adfa563df11895277630197443c5de5e.png)
The Pontrjagin dual of  , is the group
, is the group 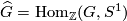 . Recall that since
. Recall that since  is a finite cyclic group the representation ring
is a finite cyclic group the representation ring 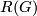 can be canonically identified with the
group ring
can be canonically identified with the
group ring 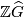 . Then we also have
. Then we also have 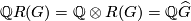 . Dividing out the regular representation corresponds to dividing out the norm element, hence
. Dividing out the regular representation corresponds to dividing out the norm element, hence 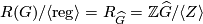 and
and 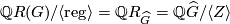 . We will also choose a preferred generator
. We will also choose a preferred generator 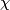 of
of 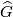 which gives the identifications
which gives the identifications
![\displaystyle \Qq R_{\widehat G} = \Qq [\chi]/\langle 1+\chi +\cdots + \chi^{N-1} \rangle.](/images/math/e/d/5/ed52fac4adb5a1af0d9857e4d35659a0.png)
Also note that one can vary the group  . Suppose that we have a subgroup
. Suppose that we have a subgroup  . Then by restricting the action we obtain from a fake lens space associated with the group
. Then by restricting the action we obtain from a fake lens space associated with the group  a fake lens space associated with the group
a fake lens space associated with the group  . Similarly we could start with a fake complex projective space which is an orbit space of a free tame action of
. Similarly we could start with a fake complex projective space which is an orbit space of a free tame action of  on
on 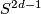 and restrict the action to
and restrict the action to 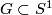 , to obtain a fake lens space associated with
, to obtain a fake lens space associated with  . Both of these operations are referred to as transfer.
. Both of these operations are referred to as transfer.
4 Invariants
For 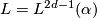 we have the following invariants:
we have the following invariants:
-
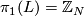 ,
, 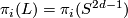 for
for 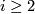 ,
,
-
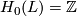 ,
, 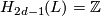 ,
, 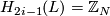 for
for 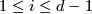 ,
, 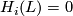 for all other values of
for all other values of  ,
,
- the
 -invariant (in the sense of homotopy theory)
-invariant (in the sense of homotopy theory) 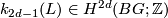 ,
,
- the Reidemeister torsion
![\Delta (L) \in \Qq R_G = \Qq [T] / \langle 1 + T + \cdots T^{N-1} \rangle](/images/math/5/6/6/566ba25449c6c6a3f455b8cf047dfac7.png) and
and
- the
 -invariant
-invariant ![\rho (L) \in \Qq R_{\widehat G}^{(-1)^d} \subset \Qq [\chi] / \langle 1 + \chi + \cdots \chi^{N-1} \rangle](/images/math/5/0/8/508fcaa8dee182bf82ea90c0b9645cff.png) .
.
When 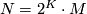 with
with 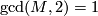 , then we have for a manifold structure
, then we have for a manifold structure 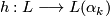 representing an element in the surgery structure set
representing an element in the surgery structure set 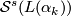 the so-called splitting invariants:
the so-called splitting invariants:
-
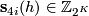 for
for 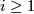 ,
,
-
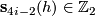 for
for 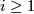 .
.
The invariants 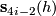 are obtained by passing to the associated manifold structure on the real projective space
are obtained by passing to the associated manifold structure on the real projective space 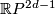 (alias restricting the action to
(alias restricting the action to 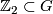 ) and taking the splitting invariant along
) and taking the splitting invariant along 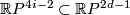 .
.
The splitting invariants 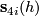 are harder to describe. One way is as follows. It follows from the calculations of the normal invariants
are harder to describe. One way is as follows. It follows from the calculations of the normal invariants 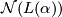 that for
that for  even the manifold structure
even the manifold structure  is normally cobordant to a manifold structure which comes from a manifold structure on the complex projective space
is normally cobordant to a manifold structure which comes from a manifold structure on the complex projective space 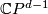 by the transfer (alias restricting the action to
by the transfer (alias restricting the action to 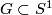 ). When
). When  is odd the same is true for the suspension manifold structure
is odd the same is true for the suspension manifold structure 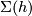 . The invariant
. The invariant 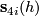 is then obtained from the splitting invariant along
is then obtained from the splitting invariant along 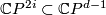 which is an integer, by taking its class modulo
which is an integer, by taking its class modulo 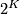 when
when  is even, and from the splitting invariant along
is even, and from the splitting invariant along 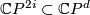 which is also an integer, by taking its class modulo
which is also an integer, by taking its class modulo 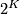 , when
, when  is odd.
is odd.
For the splitting invariants of the manifold structures on complex projective spaces see the page Fake complex projective spaces.
5 Simple homotopy theory
5.1 Preliminaries
The homotopy classification is stated in the a priori broader context of finite CW-complexes  with
with 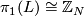 and with the universal cover homotopy equivalent to
and with the universal cover homotopy equivalent to 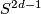 of which fake lens spaces are obviously a special case. It is convenient to make the
following definition.
of which fake lens spaces are obviously a special case. It is convenient to make the
following definition.
Definition 5.1.
Let  be a CW-complex with
be a CW-complex with 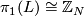 and with universal cover homotopy equivalent to
and with universal cover homotopy equivalent to 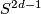 .
.
A polarization of  is a pair
is a pair 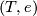 where
where  is a choice of a generator of
is a choice of a generator of 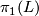 and
and  is a choice of a homotopy equivalence
is a choice of a homotopy equivalence 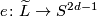 .
.
Recall the classical lens space 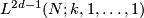 . By
. By 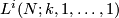 is denoted its
is denoted its  -skeleton with respect to the standard cell decomposition. If
-skeleton with respect to the standard cell decomposition. If  is odd this is a lens space, if
is odd this is a lens space, if  is even this is a CW-complex obtained by attaching an
is even this is a CW-complex obtained by attaching an  -cell to the lens space of dimension
-cell to the lens space of dimension 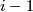 .
.
Theorem 5.2 [Wall1999, Theorem 14E.3, first part].
Let  be a finite CW-complex with
be a finite CW-complex with 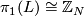 and universal cover
and universal cover 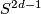 polarized by
polarized by 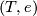 . Then there exists a map
. Then there exists a map 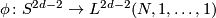 and a simple homotopy equivalence
and a simple homotopy equivalence
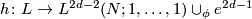
preserving the polarization, such that the 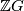 -chain complex differential on the right hand side is given by
-chain complex differential on the right hand side is given by 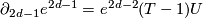 for some
for some 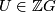 which maps to a unit
which maps to a unit 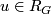 . Furthermore,
. Furthermore,  is a simple Poincare complex and its Reidemeister torsion is
is a simple Poincare complex and its Reidemeister torsion is 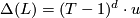 . The element
. The element  is unique up to powers of
is unique up to powers of  .
.
5.2 Homotopy classification
Theorem 5.3 [Wall1999, Theorem 14E.3, second part].
The polarized homotopy types of such  are in one-to-one correspondence with the units in
are in one-to-one correspondence with the units in 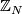 . The correspondence is given by
. The correspondence is given by 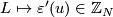 . The invariant
. The invariant 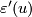 can be identified with the first non-trivial
can be identified with the first non-trivial  -invariant of
-invariant of  (in the sense of homotopy theory)
(in the sense of homotopy theory) 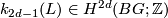 .
.
5.3 Simple homotopy classification
Theorem 5.4 [Wall1999, Theorem 14E.3, third part].
The polarized simple homotopy types of such  are in one-to-one correspondence with the equivalence classes of units in
are in one-to-one correspondence with the equivalence classes of units in 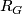 , where the equivalence relation is by the powers of
, where the equivalence relation is by the powers of  . The correspondence is given by
. The correspondence is given by 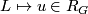 .
.
The existence of a fake lens space in the homotopy type of such  is addressed in [Wall1999, Theorem 14E.4]. Unless both
is addressed in [Wall1999, Theorem 14E.4]. Unless both  and
and  are even there always exists a manifold homotopy equivalent to the complex
are even there always exists a manifold homotopy equivalent to the complex  .
.
5.4 Fake lens spaces versus classical lens spaces
Since the units 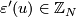 are exhausted by the lens spaces
are exhausted by the lens spaces
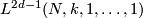 we obtain the following corollary.
we obtain the following corollary.
Corollary 5.5.
For any fake lens space 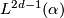 there exists
there exists 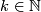 and a homotopy equivalence
and a homotopy equivalence
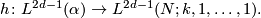
We note that the simple homotopy classification of fake lens spaces of course includes the simple homotopy classification of the classical lens spaces. For the classical lens spaces this also already yields the homeomorphism classification, the details can be found on the page about lens spaces or in [Cohen1973].
6 Homeomorphism classification
The homeomorphism classification, as already noted, is an excellent application of the non-simply connected surgery theory. Recall that for a topological manifold  the surgery theoretic homeomorphism classification of manifolds wihin the homotopy type of
the surgery theoretic homeomorphism classification of manifolds wihin the homotopy type of  is stated in terms of the simple surgery structure set
is stated in terms of the simple surgery structure set 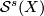 and that the primary tool for its calculation is the surgery exact sequence.
and that the primary tool for its calculation is the surgery exact sequence.
The homeomorphism classification described here of course specializes to the homeomorphism classification of the classical lens spaces as can be found on the page on lens spaces, and see also the Remark 6.5 at the end of this section.
6.1 N is odd
In terms of the structure set the main result of [Wall1999, section 14E] can be expressed as follows.
Theorem 6.1 [Wall1999, Theorem 14E.7].
If  is odd, then the reduced
is odd, then the reduced  -invariant map
-invariant map
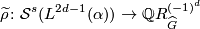
given by 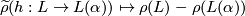 is injective.
is injective.
However, in this case, that means for  odd, Wall managed to obtain an even better result, namely the complete classification of fake lens spaces of a given dimension
odd, Wall managed to obtain an even better result, namely the complete classification of fake lens spaces of a given dimension 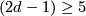 with the fundamental group
with the fundamental group 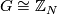 which is stated in the two theorems below.
which is stated in the two theorems below.
The classification theorem is:
Theorem 6.2 [Wall1999, Theorem 14E.7, first part].
Let 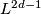 and
and 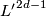 be oriented fake lens spaces with fundamental group
be oriented fake lens spaces with fundamental group  cyclic of odd order
cyclic of odd order  . Then there is an orientation preserving homeomorphism
. Then there is an orientation preserving homeomorphism 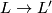 inducing the identity on
inducing the identity on  if and only if
if and only if 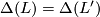 and
and 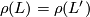 .
.
The realization theorem is:
Theorem 6.3 [Wall1999, Theorem 14E.7, second part].
Let  be cyclic of odd order. Given
be cyclic of odd order. Given 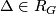 and
and 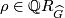 , there exists a corresponding fake lens space
, there exists a corresponding fake lens space 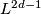 if and only if the following four statements hold:
if and only if the following four statements hold:
-
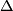 and
and  are both real (
are both real ( even) or imaginary (
even) or imaginary ( odd).
odd).
-
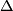 generates
generates 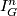 ,
, 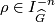 .
.
- The classes of
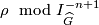 and
and 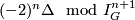 correspond under
correspond under
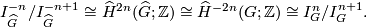
-
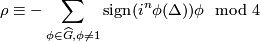 .
.
6.2 N is general
The remaining cases were addressed in [Macko&Wegner2009] and [Macko&Wegner2008] from where the following theorem, stated in tems of the structure set is taken.
Theorem 6.4 [Macko&Wegner2008, Theorem 1.2].
Let 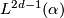 be a fake lens space with
be a fake lens space with 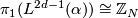 where
where 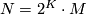 with
with 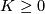 ,
,  odd and
odd and 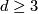 . Then we have
. Then we have
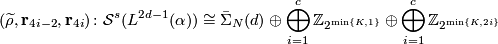
where 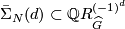 is a free abelian group. If
is a free abelian group. If  is odd then its rank is
is odd then its rank is 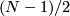 . If
. If  is even then its rank is
is even then its rank is 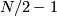 if
if 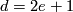 and
and 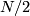 if
if 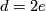 . In the torsion summand we have
. In the torsion summand we have 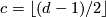 .
.
The invariant 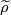 in Theorem 6.4 is the same reduced
in Theorem 6.4 is the same reduced  -invariant as above. The invariants
-invariant as above. The invariants 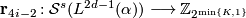 are equal to the splitting invariants
are equal to the splitting invariants 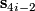 described above. The invariants
described above. The invariants 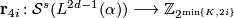 are related to the the splitting invariants
are related to the the splitting invariants 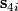 above, but they do not have a straightforward description, only an inductive one, see [Macko&Wegner2008, section 7] for more details.
above, but they do not have a straightforward description, only an inductive one, see [Macko&Wegner2008, section 7] for more details.
6.3 Some ideas from the proofs
As mentioned above the strategy in all cases is to investigate the surgery exact sequence for  .
In this case there is enough information about the normal invariants, the L-groups and the surgery obstruction so that one is left with just an extension problem. Briefly speaking the normal invariants can be calculated separately when localized at
.
In this case there is enough information about the normal invariants, the L-groups and the surgery obstruction so that one is left with just an extension problem. Briefly speaking the normal invariants can be calculated separately when localized at  , in which case a reduction to ordinary cohomology with coefficients in
, in which case a reduction to ordinary cohomology with coefficients in  and
and  is obtained, and away from
is obtained, and away from  , in which case a real reduced
, in which case a real reduced  -theory is obtained. This is well-known for
-theory is obtained. This is well-known for 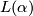 . The
. The  -groups are completely described by the representation theory of
-groups are completely described by the representation theory of  . By these calculations the surgery obstruction map can only be non-trivial in one case which is investigated in [Wall1999, Theorem 14E.4]. To proceed further it is convenient to study the relation of the surgery exact sequence to representation theory of
. By these calculations the surgery obstruction map can only be non-trivial in one case which is investigated in [Wall1999, Theorem 14E.4]. To proceed further it is convenient to study the relation of the surgery exact sequence to representation theory of  . This is done via the following commutative diagram of abelian groups and homomorphisms with exact rows.
. This is done via the following commutative diagram of abelian groups and homomorphisms with exact rows.
![\displaystyle \xymatrix{ 0 \ar[r] & {\widetilde L}^s_{2d} (G) \ar[r]^(0.4){\partial} \ar[d]_{\cong}^{G-sign} & {\mathcal S}^s (L^{2d-1}(\alpha)) \ar[r]^{\eta} \ar[d]^{\widetilde \rho}& \widetilde {\mathcal N} (L^{2d-1}(\alpha)) \ar[r] \ar[d]^{[\widetilde \rho]}& 0 \\ 0 \ar[r] & 4 \cdot R^{(-1)^d}_{\widehat G} \ar[r] & {\mathbb Q} R^{(-1)^d}_{\widehat G} \ar[r] & {\mathbb Q} R^{(-1)^d}_{\widehat G}/ 4 \cdot R^{(-1)^d}_{\widehat G} \ar[r] & 0 }](/images/math/c/e/0/ce0adafd80f8f574c18c1ece6266bff7.png)
Here the symbol 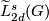 denotes the reduced
denotes the reduced  -group and the vertical isomorphism from it is the
-group and the vertical isomorphism from it is the  -signature which can be found for example in [Hambleton&Taylor2000]. The symbol
-signature which can be found for example in [Hambleton&Taylor2000]. The symbol 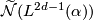 denotes the kernel of the surgery obstruction map. As mentioned above it defers from the normal invariants
denotes the kernel of the surgery obstruction map. As mentioned above it defers from the normal invariants 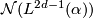 only in one case, namely when both
only in one case, namely when both  and
and  are even, and in that case the difference turns out to be a factor of
are even, and in that case the difference turns out to be a factor of  . The symbol
. The symbol ![[\widetilde \rho]](/images/math/1/a/6/1a65cbd449686c64de628afc09f22dd2.png) is the homomorphism induced by
is the homomorphism induced by 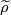 .
.
To obtain Theorem 6.1 it is shown in [Wall1999] that the map ![[\widetilde \rho]](/images/math/1/a/6/1a65cbd449686c64de628afc09f22dd2.png) is injective [Wall1999, Proposition 14E.6]. The proof proceeds by induction with respect to the dimension
is injective [Wall1999, Proposition 14E.6]. The proof proceeds by induction with respect to the dimension 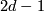 . The crucial ingredient is the transfer which produces fake lens spaces from fake complex projective spaces and the formula for the
. The crucial ingredient is the transfer which produces fake lens spaces from fake complex projective spaces and the formula for the  -invariant of fake complex projective spaces [Wall1999, Theorem 14C.4] which by naturality of the
-invariant of fake complex projective spaces [Wall1999, Theorem 14C.4] which by naturality of the  -invariant with respect to taking subgroups translates to a formula for the
-invariant with respect to taking subgroups translates to a formula for the  -invariant of the associated fake lens spaces [Wall1999, Theorem 14E.8 (c)]. The induction is possible thanks to the suspension construction described below and the multiplicativity of the
-invariant of the associated fake lens spaces [Wall1999, Theorem 14E.8 (c)]. The induction is possible thanks to the suspension construction described below and the multiplicativity of the  -invariant with respect to this construction [Wall1999, Theorem 14A.1].
-invariant with respect to this construction [Wall1999, Theorem 14A.1].
To obtain Theorem 6.4 again the map ![[\widetilde \rho]](/images/math/1/a/6/1a65cbd449686c64de628afc09f22dd2.png) is studied, first in case
is studied, first in case 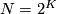 when it turns out not to be injective. The kernel of
when it turns out not to be injective. The kernel of ![[\widetilde \rho]](/images/math/1/a/6/1a65cbd449686c64de628afc09f22dd2.png) is determined in general in [Macko&Wegner2009]. The result is again obtained via fake complex projective spaces and the formula [Wall1999, Theorem 14C.4]. However, in this case the calculation is obtained via induction on
is determined in general in [Macko&Wegner2009]. The result is again obtained via fake complex projective spaces and the formula [Wall1999, Theorem 14C.4]. However, in this case the calculation is obtained via induction on  (where remember
(where remember 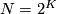 ) for any fixed
) for any fixed 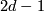 .
.
Finally, in [Macko&Wegner2008] the two special cases are combined to obtain the general cases via mostly formal arguments.
Remark 6.5.
The homeomorphism classification of classical lens spaces due to [Franz1935] and [De Rham1936], given on the lens space page, is a special case of Theorem 6.2. The additional sign and factor of  appearing in the statement of the classical theorem arise since Theorem 6.2 classifies oriented lens spaces with a fixed identification of the fundamental group. The sign allows for a change of orientation and the factor of
appearing in the statement of the classical theorem arise since Theorem 6.2 classifies oriented lens spaces with a fixed identification of the fundamental group. The sign allows for a change of orientation and the factor of  for a change of generator for the fundamental group.
for a change of generator for the fundamental group.
7 Construction and examples
Classical lens spaces are of course examples of fake lens spaces. To get fake lens spaces which are not homeomorphic to classical ones one can employ the construction of fake complex projective spaces. Note that a fake complex projective space is an orbit space of a free tame action of  on
on 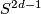 and that we obviously have
and that we obviously have 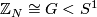 . Restricting the action to the subgroup we obtain a fake lens space. Its
. Restricting the action to the subgroup we obtain a fake lens space. Its  -invariant can be calculated by naturality using the formula for the
-invariant can be calculated by naturality using the formula for the  -invariant of the circle action.
-invariant of the circle action.
The above construction does not exhaust all the fake lens spaces. To get all of them there is a construction which produces from a given fake lens space  another fake lens space
another fake lens space 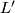 such that the difference of their
such that the difference of their  -invariants is a prescribed element
-invariants is a prescribed element
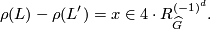
The construction is just the Wall realization from surgery theory, alias a non-simply connected generalization of the plumbing construction.
Another possibilty is to obtain fake lens spaces as orbit spaces of actions of  on Brieskorn varieties. This was pursued for example in [Orlik1969].
on Brieskorn varieties. This was pursued for example in [Orlik1969].
8 The join construction / The suspension map
Let  be a group acting freely on the spheres
be a group acting freely on the spheres 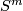 and
and  . Then the two actions extend to the join
. Then the two actions extend to the join 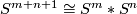 and the resulting action remains free.
and the resulting action remains free.
Given two fake lens spaces  and
and 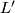 , one can pass to the universal covers, form the join and then pass to the quotient again. The resulting space is again a fake lens space. This operation is called the join and denoted by
, one can pass to the universal covers, form the join and then pass to the quotient again. The resulting space is again a fake lens space. This operation is called the join and denoted by 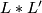 , or
, or 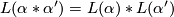 .
.
Given two manifold structures 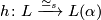 and
and 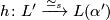 , one can pass to the induced maps of the universal covers, extend them to a map of the joins and pass to the map of quotients. This will again be a simple homotopy equivalence and hence a manifold structure
, one can pass to the induced maps of the universal covers, extend them to a map of the joins and pass to the map of quotients. This will again be a simple homotopy equivalence and hence a manifold structure 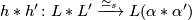
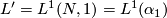 this operation is called a suspension. Taking
this operation is called a suspension. Taking 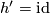 in the above paragraph defines a map
in the above paragraph defines a map 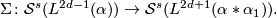
Theorem 8.1 [Wall1999, Corollary on page 228 in section 14E].
If is odd and
is odd and 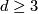 then the map
then the map 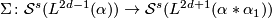
The proof is based on the classification theorem above.
The invariants 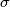 and
and  (alias desuspension obstructions) are obtained by passing to the associated fake real projective spaces via the transfer (alias restricting the group action to
(alias desuspension obstructions) are obtained by passing to the associated fake real projective spaces via the transfer (alias restricting the group action to  ) and taking the Browder-Livesay invariants described in [Lopez_de_Medrano1971] and [Wall1999, Chapter 12]. The invariant
) and taking the Browder-Livesay invariants described in [Lopez_de_Medrano1971] and [Wall1999, Chapter 12]. The invariant 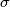 can be identified with the
can be identified with the  -invariant associated to manifolds with
-invariant associated to manifolds with 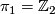 (in which case it is just an integer).
(in which case it is just an integer).
The proof is based on the classification theorem above and also on the proofs of the analogous theorems for 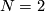 described on the page fake real projective spaces.
described on the page fake real projective spaces.
9 Further sources
The sources mentioned in the text are those where the final classification statements were presented. They built on the previous work, some of which is contained in the following papers: [Browder&Livesay1967], [Browder1970], [Petrie1970], [Petrie1970a], [Browder&Petrie&Wall1971].
10 References
- [Browder&Livesay1967] W. Browder and G. R. Livesay, Fixed point free involutions on homotopy spheres, Bull. Amer. Math. Soc. 73 (1967), 242–245. MR0206965 (34 #6781) Zbl 0276.57013
- [Browder&Petrie&Wall1971] W. Browder, T. Petrie and C. T. C. Wall, The classification of free actions of cyclic groups of odd order on homotopy spheres, Bull. Amer. Math. Soc. 77 (1971), 455–459. MR0279826 (43 #5547) Zbl 0214.22601
- [Browder1970] W. Browder, Free
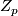 -actions on homotopy spheres, Topology of Manifolds (Proc. Inst., Univ. of Georgia, Athens, Ga., 1969), Markham, Chicago, Ill. (1970), 217–226. MR0276982 (43 #2720) Zbl 0284.57030
-actions on homotopy spheres, Topology of Manifolds (Proc. Inst., Univ. of Georgia, Athens, Ga., 1969), Markham, Chicago, Ill. (1970), 217–226. MR0276982 (43 #2720) Zbl 0284.57030
- [Cohen1973] M. M. Cohen, A course in simple-homotopy theory, Springer-Verlag, New York, 1973. MR0362320 (50 #14762) Zbl 0261.57009
- [De Rham1936] G. de Rham, Sur les nouveaux invariants topologiques de M. Reidemeister, Rec. Math. [Mat. Sbornik], Moscou, Volume 1(43), (1936), 737-742. Zbl 0016.04501
- [Franz1935] W. Franz, Über die Torsion einer Überdeckung., Journ. f. Math. 173 (1935), 245-254. Zbl 61.1350.01
- [Hambleton&Taylor2000] I. Hambleton and L. R. Taylor, A guide to the calculation of the surgery obstruction groups for finite groups, Surveys on surgery theory, Vol. 1, Princeton Univ. Press (2000), 225–274. MR1747537 (2001e:19007) Zbl 0952.57009
- [Lopez_de_Medrano1971] S. López de Medrano, Involutions on manifolds, Springer-Verlag, 1971. MR0298698 (45 #7747) Zbl 0214.22501
- [Macko&Wegner2008] T. Macko and C. Wegner, On the classification of fake lens spaces, to appear in Forum. Math. Available at the arXiv:0810.1196.
- [Macko&Wegner2009] T. Macko and C. Wegner, On fake lens spaces with fundamental group of order a power of 2, Algebr. Geom. Topol. 9 (2009), no.3, 1837–1883. MR2550097 () Zbl 1220.57020
- [Orlik1969] P. Orlik, Smooth homotopy lens spaces, Michigan Math. J. 16 (1969), 245–255. MR0248831 (40 #2081) Zbl 0182.57504
- [Petrie1970] T. Petrie, The Atiyah-Singer invariant, the Wall groups
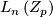 , Topology of Manifolds (Proc. Inst., Univ. of Georgia, Athens, Ga., 1969), Markham, Chicago, Ill. (1970), 490–499. MR0279829 (43 #5550) Zbl 0279.57009
, Topology of Manifolds (Proc. Inst., Univ. of Georgia, Athens, Ga., 1969), Markham, Chicago, Ill. (1970), 490–499. MR0279829 (43 #5550) Zbl 0279.57009
- [Petrie1970a] T. Petrie, Representation theory, surgery and free actions of finite groups on varieties and homotopy spheres, The Steenrod Algebra and its Applications (Proc. Conf. to Celebrate N. E. Steenrod's Sixtieth Birthday, Battelle Memorial Inst., Columbus, Ohio, 1970), Springer (1970), 250–266. MR0279828 (43 #5549) Zbl 0214.22502
- [Wall1999] C. T. C. Wall, Surgery on compact manifolds, American Mathematical Society, Providence, RI, 1999. MR1687388 (2000a:57089) Zbl 0935.57003