Whitehead torsion V (Ex)
From Manifold Atlas
(Difference between revisions)
(Created page with "<wikitex>; In the following we use the notation of {{citeD|Lück2001|Section 1.1}}. In particular, if $W$ is an $n$-manifold with boundary component $\partial_i W$ and $$\ph...") |
m |
||
| (6 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
<wikitex>; | <wikitex>; | ||
| − | |||
| − | |||
| − | |||
| − | |||
{{beginthm|Exercise}} | {{beginthm|Exercise}} | ||
| − | + | # Show that the operations (1)-(5) from {{citeD|Lück2001|Section 1.4}} used in the definition of the Whitehead group in fact yield equivalence classes of invertible matrices of arbitrary size. | |
| − | + | # Show that addition is well-defined in the Whitehead group via | |
| − | + | $$ [A] + [B] = \left [\begin{array}{cc} A & 0 \\ 0 & B \end{array} \right] = [A \cdot (B \oplus \text{Id}_{n-m})].$$ | |
| − | + | Here $A$ and $B$ are invertible matricies over the group ring $\Zz[\pi]$, $A$ is an $n \times n$ matrix, $B$ is an $m \times m$ matrix with $n \geq m$, $O$ denotes the zero $n \times m$ and $m \times n$ matricies and $\cdot$ denotes matrix multiplication. | |
| − | + | # Show that $Wh(e)$ is trivial. | |
| − | + | ||
| − | + | ||
| − | Show that | + | |
| − | $$ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | $$ | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
{{endthm}} | {{endthm}} | ||
</wikitex> | </wikitex> | ||
[[Category:Exercises]] | [[Category:Exercises]] | ||
| + | [[Category:Exercises without solution]] | ||
Latest revision as of 15:05, 1 April 2012
Exercise 0.1.
- Show that the operations (1)-(5) from [Lück2001, Section 1.4] used in the definition of the Whitehead group in fact yield equivalence classes of invertible matrices of arbitrary size.
- Show that addition is well-defined in the Whitehead group via
![\displaystyle [A] + [B] = \left [\begin{array}{cc} A & 0 \\ 0 & B \end{array} \right] = [A \cdot (B \oplus \text{Id}_{n-m})].](/images/math/5/f/5/5f5914c195320893b9a3bd7cca8703d6.png)
Here  and
and  are invertible matricies over the group ring
are invertible matricies over the group ring ![\Zz[\pi]](/images/math/5/9/a/59abcee2c0404c04e89fb508a53c9890.png) ,
,  is an
is an 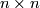 matrix,
matrix,  is an
is an 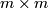 matrix with
matrix with 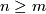 ,
, 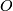 denotes the zero
denotes the zero 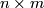 and
and 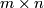 matricies and
matricies and  denotes matrix multiplication.
denotes matrix multiplication.
- Show that
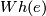 is trivial.
is trivial.