Whitehead torsion V (Ex)
In the following we use the notation of [Lück2001, Section 1.1]. In particular, if  is an
is an  -manifold with boundary component
-manifold with boundary component 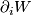 and
and
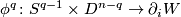
is an embedding then 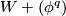 denotes the manifold of obtained from
denotes the manifold of obtained from  by attaching a
by attaching a  -handle along
-handle along 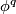 :
:
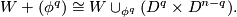
Exercise 0.1.
Let 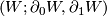 be an
be an  -dimensional cobordism, and suppose that, relative to
-dimensional cobordism, and suppose that, relative to 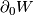 , we have
, we have
![\displaystyle W \cong \partial_0 W \times [0,1] + \sum_{i=1}^{p_0} (\phi^0_i) + \ldots + \sum_{i=1}^{p_n} (\phi^n_i).](/images/math/d/f/1/df100365c240212a8cc86891e51cf698.png)
Show that there is another diffeomorphism, relative to 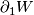 , which is of the following form:
, which is of the following form:
![\displaystyle W \cong \partial_1 W \times [0,1] + \sum_{i=1}^{p_n} (\psi^0_i) + \ldots + \sum_{i=1}^{p_0} (\psi^n_i).](/images/math/0/4/c/04c84744c20cf6a1eadb8f81494234f3.png)
The important part is that for each  -handle in the first handlebody decomposition, we have an
-handle in the first handlebody decomposition, we have an 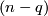 -handle in the second, dual handlebody decomposition.
-handle in the second, dual handlebody decomposition.
Comment 0.2. If one approaches this exercise using Morse functions (and their relation to handlebody decompositions), the above is almost trivial (Question: Why?). The actual intention of this exercise is to go through the details of the rather direct approach outlined in [Lück2001, pp.17-18]. While this is a bit tedious, it provides a good opportunity to get more familiar with handlebody attachments and the like.
Exercise 0.3.
- Show that the operations (1)-(5) from [Lück2001, Section 1.4] used in the definition of the Whitehead group in fact yield equivalence classes of invertible matrices of arbitrary size.
- Show that
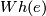 is trivial.
is trivial.