Talk:Thom spaces (Ex)
From Manifold Atlas
(Difference between revisions)
| Line 1: | Line 1: | ||
<wikitex>; | <wikitex>; | ||
| − | Part 1 | + | '''Part 1''' |
We define | We define | ||
| Line 20: | Line 20: | ||
where $\mathrm{arg}(z)\in(0,2\pi)$. | where $\mathrm{arg}(z)\in(0,2\pi)$. | ||
| − | Part 2 | + | '''Part 2''' |
If $i$: $M\to\mathbb{R}^{n+k}$ is an embedding, we denote by $j$: $M\to\mathbb{R}^{n+k+1}$ the composition | If $i$: $M\to\mathbb{R}^{n+k}$ is an embedding, we denote by $j$: $M\to\mathbb{R}^{n+k+1}$ the composition | ||
| Line 44: | Line 44: | ||
$$ | $$ | ||
| − | Part 3 | + | '''Part 3''' |
Let the embeddings $i$ and $j$ be as in Part 2. | Let the embeddings $i$ and $j$ be as in Part 2. | ||
| Line 68: | Line 68: | ||
$$ | $$ | ||
| − | Part 4 | + | '''Part 4''' |
Of course one can do similar things for non oriented manifolds or spin manifolds. | Of course one can do similar things for non oriented manifolds or spin manifolds. | ||
One only has to modify the definition of $\Omega_n(X)$ and use the corresponding universal bundle instead of $\xi_k$. | One only has to modify the definition of $\Omega_n(X)$ and use the corresponding universal bundle instead of $\xi_k$. | ||
</wikitex> | </wikitex> | ||
Latest revision as of 12:17, 2 April 2012
Part 1
We define
![\displaystyle \mathrm{Th}(\xi_1)\wedge\mathrm{Th}(\xi_2)\to\mathrm{Th}(\xi_1\times\xi_2),\quad [v_1,v_2]\mapsto \left\{ \begin{array}{ll}\infty, & \textrm{if }v_1=\infty\textrm{ or }v_2=\infty \\ v_1\oplus v_2, & \textrm{else}\end{array} \right.](/images/math/3/c/e/3ce228e8d0f4c73fd415a51f186f7a96.png)
and
![\displaystyle S^1\wedge\mathrm{Th}(\xi)\to\mathrm{Th}(\xi\oplus\underline{\mathbb{R}}),\quad [z,v]\mapsto \left\{ \begin{array}{ll}\infty, & \textrm{if }z=1\textrm{ or }v=\infty \\ v\oplus\cot(\mathrm{arg}(z)/2), & \textrm{else}\end{array} \right.](/images/math/5/7/7/577cb8dd5bb5cf34994d6da143cfabe8.png)
where 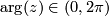 .
.
Part 2
If 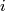 :
: 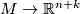 is an embedding, we denote by
is an embedding, we denote by 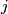 :
: 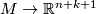 the composition
of
the composition
of 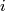 with the inclusion
with the inclusion 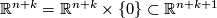 .
In particular the normal bundles are related by
.
In particular the normal bundles are related by 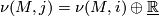 .
The bundle map
.
The bundle map 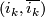 induces
induces
![\displaystyle \Omega_n(\overline{i_k}): \Omega_n(\gamma_k)\to\Omega_n(\gamma_{k+1}),\quad [M,i,f,\overline{f}]\mapsto[M,j,i_k\circ f,\overline{i_k}\circ(\overline{f}\oplus\mathrm{id}_{\underline{\mathbb{R}}})].](/images/math/a/6/9/a69fd3d13577cb882a050cf8bc388681.png)
From the definition
![\displaystyle V_k:\quad\Omega_n(\gamma_k)\to\Omega_n(X),\quad [M,i,f,\overline{f}]\mapsto[M,\mathrm{pr}_X\circ f]](/images/math/0/c/8/0c87931a611dc39464d056b6915d5216.png)
we find for all 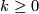
![\displaystyle (V_{k+1}\circ\Omega_n(\overline{i_k}))([M,i,f,\overline{f}]) =[M,\mathrm{pr}_X\circ i_k\circ f] =[M,\mathrm{pr}_X\circ(\mathrm{id_X\times j_k})\circ f] =[M,\mathrm{pr}_X\circ f] =V_k([M,i,f,\overline{f}]).](/images/math/b/0/7/b07fde506114bdcef9ebefe33c209406.png)
Part 3
Let the embeddings 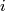 and
and 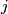 be as in Part 2.
Define the collapse maps
be as in Part 2.
Define the collapse maps
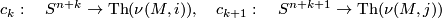
as in [Lück2001, page 57]. Then we have 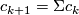 .
For all
.
For all 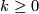 we obtain
we obtain
![\displaystyle (P_n(\gamma_{k+1})\circ\Omega_n(\overline{i_k}))([M,i,f,\overline{f}]) =P_n(\gamma_{k+1})([M,j,i_k\circ f,\overline{i_k}\circ(\overline{f}\oplus\mathrm{id}_{\underline{\mathbb{R}}})]) =[\mathrm{Th}(\overline{i_k}\circ(\overline{f}\oplus\mathrm{id}_{\underline{\mathbb{R}}}))\circ c_{k+1}] =[\mathrm{Th}(\overline{i_k})\circ\mathrm{Th}(\overline{f}\oplus\mathrm{id}_{\underline{\mathbb{R}}})\circ c_{k+1}]](/images/math/8/6/9/8697c6b951848870ab744d9e6ad3c849.png)
and
![\displaystyle (s_k\circ P_n(\gamma_k))([M,i,f,\overline{f}]) =s_k([\mathrm{Th}(\overline{f})\circ c_k]) =[\mathrm{Th}(\overline{i_k})\circ\Sigma(\mathrm{Th}(\overline{f})\circ c_k)] =[\mathrm{Th}(\overline{i_k})\circ\mathrm{Th}(\overline{f}\oplus\mathrm{id}_{\underline{\mathbb{R}}})\circ c_{k+1}].](/images/math/d/c/0/dc06fc7b10f507dce102234318cf09e9.png)
Part 4
Of course one can do similar things for non oriented manifolds or spin manifolds.
One only has to modify the definition of 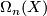 and use the corresponding universal bundle instead of
and use the corresponding universal bundle instead of 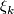 .
.