Talk:Thom spaces (Ex)
(Difference between revisions)
| Line 30: | Line 30: | ||
[M,i,f,\overline{f}]\mapsto[M,j,i_k\circ f,\overline{i_k}\circ(\overline{f}\oplus\mathrm{id}_{\underline{\mathbb{R}}})]. | [M,i,f,\overline{f}]\mapsto[M,j,i_k\circ f,\overline{i_k}\circ(\overline{f}\oplus\mathrm{id}_{\underline{\mathbb{R}}})]. | ||
$$ | $$ | ||
| + | From the definition | ||
| + | $$ | ||
| + | V_k:\quad\Omega_n(\gamma_k)\to\Omega_n(X),\quad | ||
| + | [M,i,f,\overline{f}]\mapsto[M,\mathrm{pr}_X\circ f] | ||
| + | $$ | ||
| + | we find for all $k\geq0$ | ||
| + | $$ | ||
| + | (V_{k+1}\circ\Omega_n(\overline{i_k}))([M,i,f,\overline{f}]) | ||
| + | =[M,\mathrm{pr}_X\circ i_k\circ f] | ||
| + | =[M,\mathrm{pr}_X\circ(\mathrm{id_X\times j_k})\circ f] | ||
| + | =[M,\mathrm{pr}_X\circ f] | ||
| + | =V_k([M,i,f,\overline{f}]). | ||
| + | $$ | ||
</wikitex>; | </wikitex>; | ||
Revision as of 09:41, 2 April 2012
Part 1
We define
![\displaystyle \mathrm{Th}(\xi_1)\wedge\mathrm{Th}(\xi_2)\to\mathrm{Th}(\xi_1\times\xi_2),\quad [v_1,v_2]\mapsto \left\{ \begin{array}{ll}\infty, & \textrm{if }v_1=\infty\textrm{ or }v_2=\infty \\ v_1\oplus v_2, & \textrm{else}\end{array} \right.](/images/math/3/c/e/3ce228e8d0f4c73fd415a51f186f7a96.png)
and
![\displaystyle S^1\wedge\mathrm{Th}(\xi)\to\mathrm{Th}(\xi\oplus\underline{\mathbb{R}}),\quad [z,v]\mapsto \left\{ \begin{array}{ll}\infty, & \textrm{if }z=1\textrm{ or }v=\infty \\ v\oplus\cot(\mathrm{arg}(z)/2), & \textrm{else}\end{array} \right.](/images/math/5/7/7/577cb8dd5bb5cf34994d6da143cfabe8.png)
where 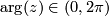 .
.
Part 2
If 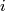 :
: 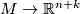 is an embedding, we denote by
is an embedding, we denote by 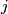 :
: 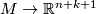 the composition
of
the composition
of 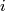 with the inclusion
with the inclusion 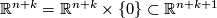 .
In particular the normal bundles are related by
.
In particular the normal bundles are related by 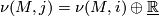 .
The bundle map
.
The bundle map 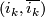 induces
induces
![\displaystyle \Omega_n(\overline{i_k}): \Omega_n(\gamma_k)\to\Omega_n(\gamma_{k+1}),\quad [M,i,f,\overline{f}]\mapsto[M,j,i_k\circ f,\overline{i_k}\circ(\overline{f}\oplus\mathrm{id}_{\underline{\mathbb{R}}})].](/images/math/a/6/9/a69fd3d13577cb882a050cf8bc388681.png)
From the definition
![\displaystyle V_k:\quad\Omega_n(\gamma_k)\to\Omega_n(X),\quad [M,i,f,\overline{f}]\mapsto[M,\mathrm{pr}_X\circ f]](/images/math/0/c/8/0c87931a611dc39464d056b6915d5216.png)
we find for all 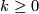
![\displaystyle (V_{k+1}\circ\Omega_n(\overline{i_k}))([M,i,f,\overline{f}]) =[M,\mathrm{pr}_X\circ i_k\circ f] =[M,\mathrm{pr}_X\circ(\mathrm{id_X\times j_k})\circ f] =[M,\mathrm{pr}_X\circ f] =V_k([M,i,f,\overline{f}]).](/images/math/b/0/7/b07fde506114bdcef9ebefe33c209406.png)